И теоремы Муавра-Лапласа как следствия из нее

Центральная предельная теорема. Пусть случайные величины 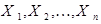– независимы и одинаково распределены. Тогда закон распределения их суммы 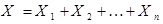неограниченно приближается к нормальному при неограниченном увеличении числа n эти х случайных величин.

Отметим, что центральная предельная теорема является частным случаем более общего утверждения – теоремы Ляпунова (подробнее см. учебник Н.Ш. Кремера).

Следствие. Биномиальный закон распределения неограниченно приближается к нормальному при неограниченном увеличении параметра n этого закона.

Доказательство. Пусть случайная величина Х – биномиально распределена с параметрами n и p. Рассмотрим сначала тот конкретный пример, когда Х – число наступлений некоторого события А в n повторных независимых испытаниях, в каждом из которых это событие наступает с вероятностью p. Введем в рассмотрение случайные величины 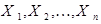такие, что – число наступлений события А в i –ом испытании, где 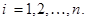Случайная величина принимает значение 1, если в i –ом испытании событие А наступило и значение 0 – в противном случае. Сумма случайных величин принимает значение m тогда и только тогда, когда число Х наступлений события А в n испытаниях равно m., т.е.

.

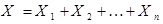Тогда по центральной предельной теореме для случайной величины Х получаем требуемое утверждение. Аналогично данное Следствие доказывается и в общем случае.

Данное Следствие при работе с биномиально распределенными случайными величинами (при достаточно больших n) позволяет использовать формулы, известные для нормально распределенных случайных величин. Именно это и происходит при применении теорем Муавра-Лапласа. Так, заменяя в формуле (1) из § 4.2 а и 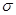математическим ожиданием и средне квадратическим отклонением биномиально распределенной случайной величины ( 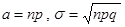см. § 3.3), обозначая также 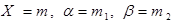, приходим к интегральной теореме Муавра-Лапласа.

Геометрически приближение биномиального распределения к нормальному означает, что с ростом n точки плоскости с координатами 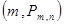неограниченно приближаются к кривой 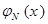плотности нормального закона (здесь m –неотрицательное целое, не превосходящее n, значение 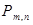вычисляется по формуле Бернулли; см. рис. 11).

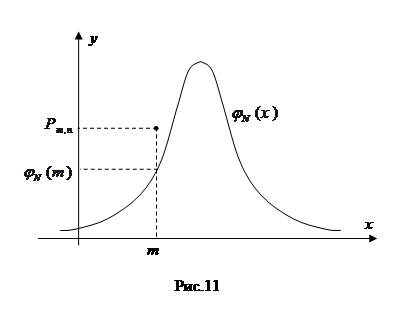Тогда справедливо приближенное равенство

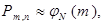
где 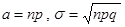, которое, записанное явно, и есть локальная теорема Муавра-Лапласа.