Первое доказательство теоремы Эйлера.

Введение

Замечательная теорема о выпуклых многогранниках, которой посвящена эта статья, была опубликована Л. Эйлером (1707-1783) в 1758 году. Позднее обнаружилось, что она была известна Р. Декарту (1596-1650) почти за 100 лет до Эйлера. Сейчас принято называть теоремой (или формулой) Эйлера соотношение между числами вершин, ребер и граней многогранника, а теоремой Декарта - утверждение о сумме его плоских углов, которое легко следует из теоремы Эйлера (формулировку теоремы Декарта см. ниже в задаче 5).

Мы дадим здесь два доказательства теоремы Эйлера и некоторые следствия из нее.

Теорема Эйлера

Теорема Эйлера. Для любого выпуклого многогранника выполняется равенство

B - P + Г = 2, (1)

где буквы B, P и Г обозначают соответственно число его вершин, ребер и граней.

Например, для куба имеем B = 8, P = 12, Г = 6, для многогранника на рис. 1 B = 5, P = 9, Г = 6, и соотношение (1) выполнено.

Лемма

Лемма. Если в пространстве заданы прямые L ₁, L ₂,..., L_m, то можно построить плоскость, не параллельную ни одной из этих прямых.

Доказательство. Возьмем в пространстве точку O и проведем через нее произвольную плоскость Q и прямые L' ₁, L' ₂,..., L'_m, соответственно параллельные прямым L ₁, L ₂,..., L_m. Кроме того, в плоскости Q через точку O проведем прямую M, отличную от всех прямых L'_i (i = 1,... m). Пусть a _i - угол между плоскостью Q и прямой L'_i (i = 1,... m). Мы считаем, что 0 £ a _i £ p/2. Если все прямые L'_i лежат в Q, т. е. если все углы a _i = 0, то искомой будет любая плоскость, проведенная через M и отличная от Q. В противном случае среди углов a _i выберем наименьший положительный; пусть это будет, например, a₁. Теперь через прямую M проведем плоскость R, образующую с Q положительный угол, меньшей чем a₁. Ясно, что R не содержит ни одной из прямых L'_i, и поэтому является искомой плоскостью.

Первое доказательство теоремы Эйлера.

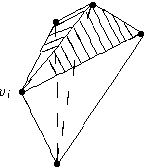
Первое доказательство теоремы Эйлера. Рассмотрим множество всех прямых, каждая из которых соединяет пару вершин многогранника. Пользуясь леммой, проведем плоскость, не параллельную ни одной прямой этой указанного множества. Об этой плоскости сделаем два предположения: будем считать, что она, во-первых, горизонтальна (этого всегда можно добиться, поворачивая нужным образом все пространство), во-вторых, расположена ниже нашего многогранника. Тогда все его вершины располагаются на разной высоте над этой плоскостью, и мы можем пронумеровать вершины в порядке возрастания их высот; пусть v ₁ обозначает самую нижнюю вершину, v ₂ - следующую за ней по высоте, наконец, v_n - самую верхнюю (здесь n равно числу вершин B). Обозначим через Г_i (i = 1,... n) число граней многогранника, для которых точка v_i является самой нижней вершиной, или, другими словами, которые " выходят" ' вверх из вершины v_i. Пусть P_i (i = 1,... n) обозначает число ребер многогранника, которые имеют вершину v_i своим нижним концом (или " выходят" вверх из этой вершины).

Рассмотрим самую нижнюю вершину v_i. К ней примыкает одинаковое число ребер и граней, и все они выходят из нее вверх. Поэтому

P ₁ = Г ₁ (2)

Рис. 1	Рис. 2

Пусть v_i - промежуточная вершина многогранника, т. е. такая, что 2 £ i £ n - 1. Рассмотрим все ребра и грани, выходящие из нее вверх. Можно представить себе, что все они " веером" расходятся из v_i (см. рис. 1, где веер состоит из трех ребер и двух заштрихованных граней). Для нас несущественно, сколько именно в таком веере ребер и граней; важно лишь, что для их чисел выполнено соотношение

P_i = Г_i = 1, i = 2, 3,..., n - 1. (3)

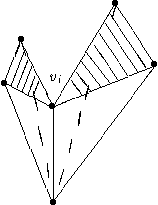
Веер может состоять только из одного ребра; так будет, например, при i = n - 1. Именно здесь используется выпуклость многогранника: благодаря ей указанный веер будет только один. Если нет выпуклоскти, вееров может быть несколько, и тогда равенство (3) нарушается (см. рис. 2: два тетраэдра, приставленные друг к другу вдоль их общего ребра). Для самой верхней вершины v_n нет ребер и граней, выходящих из нее вверх, поэтому P_n = Г_n = 0.

Общее число ребер многогранника равно P = P ₁ + P ₂ +... + P_{n -1}, а общее число его граней равно Г = Г ₁ + Г ₂ +... + Г_{n -1}. Поэтому, используя равенства (2) и (3), получаем

B - P + Г = n - (P ₁ + P ₂ +... + P_{n - 1}) + (Г ₁ + Г ₂ +... + Г_{n - 1}) =

n - (P ₁ + P ₂ +... + P_{n - 1}) + P ₁ + (P ₂ - 1) +... +(P_{n - 1} - 1) =

n - (P ₁ + P ₂ +... + P_{n - 1}) + (P ₁ + P ₂ +... + P_{n - 1}) - (n - 2) = 2.