Задачи математической статистики

3.2.1 Первый этап – сбор и первичная обработка данных

Для того, чтобы сделать вывод о поведении некоторой совокупности объектов, необходимо провести обследование каждого из этих объектов. В теории статистики различают два вида статистического наблюдения по степени полноты охвата: сплошное и несплошное. Сплошным называется такое наблюдение, при котором обследуется вся статистическая совокупность. Такая совокупность получила название генеральной. Статистическая практика показала, что идеально сплошных наблюдений почти не удается получить, так как определенная часть совокупности по различным причинам ускользает от наблюдения. Тем не менее, если степень охвата наблюдением очень велика, то наблюдение считается сплошным.

Несплошным называется такое наблюдение, при котором обследуется определенная часть единиц совокупности. Результатом такого наблюдения является выборочная совокупность. Выборочной совокупностью или просто выборкой называется совокупность случайно отобранных объектов. Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности, например, если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N =1000, а объем выборки n =100.

Несплошное наблюдение может выполняться различными методами: выборочным, направленного отбора, методом основного массива.

Среди названных методов наиболее распространен выборочный метод наблюдения, сущность которого заключается в случайном отборе некоторого числа единиц статистической совокупности при строго объективном подходе к их отбору. Выборочный метод наблюдения позволяет по отобранной совокупности судить о характеристиках генеральной совокупности. Наиболее важным принципом этого метода является равновозможность отбора, сущность которого заключается в том, что каждой единице обеспечена равная возможность быть отобранной, т. е. ни одна единица при отборе не обладает преимуществом перед другой.

Выборочный метод наблюдения дает возможность получать случайную выборку, для статистической обработки которой используется теория вероятностей.

Одна из важнейших теорем теории вероятностей, сформулированная П. Л. Чебышевым, составляет теоретическую основу выборочного метода наблюдения. Применительно к данному методу она может быть записана в следующем виде:

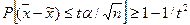(3.1)

где Р - символ вероятности;

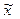- средняя для выборочной совокупности;

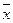- средняя для генеральной совокупности;

t - множитель, указывающий на вероятность ошибки;

α - среднее квадратическое отклонение в генеральной совокупности;

n - объем случайной выборки.

При практическом использовании теоремы П. Л. Чебышева дисперсию для генеральной совокупности α ² заменяют выборочной дисперсией α ², так как первую подсчитать невозможно.

Множитель t, связанный с вероятностью Р, называется также нормированным отклонением, или стандартизованной разностью. Отношение (α /√ n) часто обозначается через μ и выражает среднюю ошибку выборки.

Теорема П. Л. Чебышева формулируется так: с вероятностью, сколь угодно близкой к единице (достоверности), можно утверждать, что при достаточно большом объеме выборки n и ограниченной дисперсии генеральной совокупности α ² разность между выборочной средней 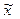и генеральной средней 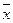будет сколь угодно мала.

Генеральная и выборочная совокупности характеризуются рядом статистических показателей. В их числе можно назвать генеральную и выборочную средние, генеральное и выборочное среднее квадратическое отклонения и т. д.

При использовании выборочного метода наблюдения производят отбор единиц из генеральной совокупности. Систему организации отбора называют способом отбора. В зависимости от того, сколько раз отобранная единица участвует в дальнейшей выборке, различают два вида отбора: повторный и бесповторный.

Повторным называется такой вид отбора, при котором отобранная в первый раз единица возвращается обратно в генеральную совокупность и вновь участвует в выборке. Здесь мы наблюдаем постоянную вероятность попадания в выборку всех единиц совокупности.

Бесповторным называется такой вид отбора, при котором отобранная в первый раз единица в генеральную совокупность обратно не возвращается. Здесь мы наблюдаем переменную вероятность попадания в выборку каждой новой единицы.

Повторный и бесповторный отборы могут производиться разными способами. При выполнении статистических исследований различают пять способов отбора: собственно случайный, механический, типический, серийный и комбинированный.

Собственно случайный отбор ориентирован на выборку единиц из генеральной совокупности без какого-либо расчленения ее на части или группы и осуществляется наудачу. Он не зависит от изучаемых признаков и сохраняет принцип равновозможности отбора. Случайный отбор осуществляется при помощи жеребьевки или на основе таблиц случайных чисел и позволяет получать объективную оценку генеральной совокупности. Этот способ дает собственно случайную выборку. При большом объеме генеральной совокупности описанный процесс оказывается очень трудоемким.

При механическом отборе генеральная совокупность делится на число групп, соответствующих объему выборки и из каждой группы в выборку отбирается одна единица. Отбор производится в каком-либо механическом порядке. Например, в выборку попадают каждая пятая, каждая десятая и т. д. единицы при определенном их положении в генеральной совокупности.

При типическом отборе генеральная совокупность делится по некоторому признаку на типические группы и из каждой группы производится случайный отбор единиц. При этом, если отбирают некоторое число единиц, непропорциональное численности типической группы, то такой выбор называют непропорциональным типическим отбором, а в противном случае - пропорциональным. Типическим отбором пользуются тогда, когда обследуемый признак заметно колеблется в различных типических частях генеральной совокупности.

При серийном отборе производится выборка не единиц совокупности, а некоторых групп или серий. Внутри отобранных серий осуществляется сплошное наблюдение. При этом серии могут быть равновеликими и неравновеликими. Серийным отбором пользуются тогда, когда обследуемый признак колеблется в различных сериях незначительно.

При комбинированном отборе предполагается использовать одновременно несколько способов, например, серийный и случайный. В этом случае сначала генеральная совокупность разбивается на серии, а затем по отобранным сериям производится случайный отбор единиц [15].

Выборочный метод наблюдения, как и другие статистические методы, должен учитывать неточности наблюдений, которые называются ошибками наблюдения. Они состоят из ошибок регистрации и ошибок репрезентативности.

Ошибки, возникшие из-за неправильных и неточных сведений, называются ошибками регистрации. Они появляются в результате недостаточного понимания существа вопроса, ошибок регистраторов, пропуска или повторного счета некоторых единиц совокупности. Ошибки регистрации бывают двух видов: преднамеренные и непреднамеренные. Ошибки первого вида сознательно направлены на искажение действительности. К ним можно отнести приписки, скрытие резервов и т. д. В составе непреднамеренных ошибок различают систематические и случайные ошибки. Систематические ошибки обусловлены причинами, действующими в каком-либо одном направлении, которое приводит к искажению статистической информации, например округление цифр, пропуски единиц наблюдения, а также ошибки субъективных впечатлений. Случайные ошибки уравновешивают друг друга и не оказывают заметного влияния на проведение наблюдения.

Ошибки репрезентативности характеризуют разность между размером изучаемых признаков в генеральной и выборочной совокупности. Ошибки репрезентативности присущи только несплошному наблюдению. Они также делятся на два вида: систематические и случайные ошибки репрезентативности. Ошибки первого вида возникают из-за неправильного, тенденциозного отбора единиц наблюдения и приводят к нарушению основного принципа построения научно обоснованной выборки, т. е. нарушается принцип равновозможного отбора единиц. Ошибки второго вида, как правило, зависят от степени однородности статистической совокупности.

Среди задач, которые решаются на основе выборочного метода наблюдений, необходимо выделить изучение и измерение случайных ошибок репрезентативности. Эта задача заключается в определении средней или стандартной ошибки выборки, которая представляет собой среднеквадратическое отклонение возможных значений выборочной средней от генеральной средней, взвешенных по вероятностям их возникновения. Аналитические формулы для расчета средней ошибки выборки μ подбирают исходя из способа отбора:

для случайного повторного отбора

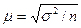(3.2)

где σ - среднее квадратическое отклонение выборки;

n - численность выборки.

для случайной бесповторной выборки

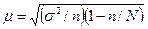(3.3)

где N - численность большой совокупности, из которой производится отбор.

для механической выборки - формулы (3.2), (3.3);

для непропорционального типического отбора:

при повторной выборке

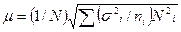(3.4)

где σ ² _i - выборочная дисперсия i-й типической группы;

N - численность i-й типической группы;

n - численность выборки из i-й типической группы.

при бесповторной выборке

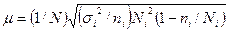(3.5)

для пропорционального типического отбора, который является случаем типической выборки с любыми пропорциями отбора:

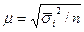(3.6)

где 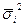- средняя из выборочных дисперсий i-х типических групп.

для аналогичной бесповторной выборки

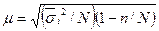(3.7)

Разбивка на типические группы позволяет избежать влияния межгрупповой вариации на точность выборки, так как в типическую выборку обязательно входят представители всех групп. Поэтому в формулах (3.6) и (3.7), в отличие от формул (3.1) и (3.2), ошибка выборки находится в зависимости не от общей дисперсии σ ², а от средней дисперсии типических групп ^.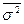

При выполнении статистических исследований возможны случаи, когда типический отбор производится пропорционально не численности единиц в типических группах, а пропорционально колеблемости признака. Такой отбор носит название типического отбора, пропорционального дифференциации признака и средняя ошибка выборки для него находится по формулам:

при повторном отборе

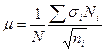(3.8)

при бесповторном отборе

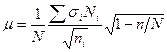(3.9)

где σ _i - среднее квадратическре отклонение в выборке из i-й типической группы.

Типический отбор с учетом дифференциации признака дает наиболее благоприятные результаты. При серийном отборе его точность уже зависит не от величины общей дисперсии, которую мы наблюдаем при случайном отборе, а от межсерийной дисперсии, или дисперсии групповых средних [24].

Средние ошибки выборки при серийном методе отбора с равновеликими сериями получают по формулам:

при повторном отборе

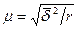(3.10)

при бесповторном отборе

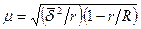(3.11)

где 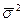- межсерийная или межгрупповая дисперсия средних значений;

r - число отобранных серий;

R - число серий в генеральной совокупности.

В свою очередь межсерийная или межгрупповая дисперсия определяется по формуле

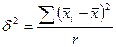(3.12)

где 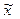- средняя величина в i-й серии;

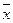- общая средняя величина во всех сериях.

Средняя ошибка выборки при различных комбинациях способов отбора исчисляется по-разному. Например, при комбинировании серийного отбора с равными сериями со случайным отбором средняя ошибка выборки определяется по формулам:

при повторном отборе

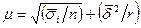(3.13)

при бесповторном отборе

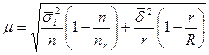(3.14)

где n_r - общее число единиц, попавших в выборку при отборе серий;

n - число единиц, попавших в выборку из серий.

При этом

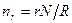(3.15)

где r - число отобранных серий;

N - численность совокупности, из которой производится отбор;

R - число серий в генеральной совокупности.

Комбинированный отбор может быть многоступенчатым, если выборка осуществляется в несколько этапов. Когда же число ступеней отбора больше двух, то среднюю ошибку выборки при равной численности групп можно определить из выражения

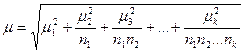(3.16)

где μ ₁, μ ₂, μ ₃, ….μ _k. - средние ошибки выборки при отдельных ступенях;

n_1, n₂, n₃, ….n_k - численности выборок на соответствующих ступенях.

При использовании выборочного метода наблюдений возникает вопрос о необходимой численности выборки, которая может быть получена исходя из допустимой ошибки для определенного способа отбора. Кроме того, необходимая численность выборки устанавливается по разным методикам для выборочного наблюдения, в котором находится средний размер признака в совокупности для доли единиц, обладающих данным признаком. Разные методики основываются на разных методах вычисления меры колеблемости для варьирующего и альтернативного признака. Меру колеблемости для варьирующего признака приблизительно можно определить через размах колебаний R либо более точно - на основании результатов предыдущих опытов. В этих условиях среднее квадратическое отклонение рассчитывается по формуле

σ = R / 6 (3.17)

Следовательно, с вероятностью F(t) = 0, 997 можно утверждать, что размах вариации R при нормальном распределении признака соответствует 6* σ.

Если необходимая численность выборки определяется для альтернативного признака и неизвестна, хотя бы приблизительно, доля выборки, то необходимая численность соответствует дисперсии σ ² = 0, 25, т. е.

n = 0, 25 t² / ∆ ² (3.18)

где n - необходимая численность выборки;

t - параметр, связанный с вероятностью Р;

∆ - предельная ошибка выборки.

Рассмотрим определение необходимой численности выборки при собственно случайном способе отбора:

для повторной выборки

n = σ ² t² / ∆ ² (3.19)

для бесповторной выборки

n = σ ² t² N / (∆ ² N + σ ² t²) (3.20)

где N — объем генеральной совокупности.

Для механического способа отбора необходимая численность выборки определяется по формуле (3.20).

При типическом отборе различают три способа расчета необходимой численности выборки. Первый способ относится к типическому отбору, который непропорционален объему групп. В этом случае общее число отбираемых единиц делят на число типических групп, и полученное частное характеризует численность отбора из каждой типической группы. Второй способ относится к типическому отбору, который пропорционален объему групп. Необходимая численность выборки в этом случае находится по формуле:

n_i = n (N_i / N) (3.21)

где n_i - необходимая численность выборки для i-й типической группы;

n - общий объем выборки;

N_i - объем 1-й типической группы;

N - объем генеральной совокупности.

Третий способ относится к типическому отбору, который пропорционален дифференциации признака. В этих условиях необходимая численность выборки находится из выражения:

n_i = n N_i σ _i / (∑ N_i σ _i) (3.22)

где σ _i – среднеквадратическое отклонение в i-й типической группе.

При серийном способе отбора с равновеликими сериями необходимая численность выборки определяется по формулам случайного отбора:

для повторной выборки

r = б ² t² / ∆ ² (3.23)

где r - число отобранных серий;

t - параметр, связанный с вероятностью Р;

б² - межгрупповая или межсерийная дисперсия;

∆ - предельная ошибка выборки.

для бесповторной выборки

r = б ² t² R / (∆ ² R + б ² t²) (3.24)

где R - число серий в генеральной совокупности.

Анализируя различные способы определения необходимой численности выборки, можно сделать вывод, что все они основываются на формуле предельной ошибки выборки для разных способов отбора. Выборочный метод наблюдения находит широкое применение в статистической практике. На его основе проводятся обследования бюджетов семей рабочих, занятых в строительстве, состава их семей, учет посевных площадей и поголовья скота в личных хозяйствах населения, выборочная разработка данных для переписей населения.

Применительно к строительству выборочный метод наблюдения используется для обследования затрат на производство строительно-монтажных работ; заработной платы рабочих по профессиям и тарифным разрядам, инженерно-технических работников и служащих по должностям. Кроме того, широкое распространение получили статистические методы контроля качества строительной продукции и продукции предприятий материально-технической базы строительства, основанные на выборочном методе наблюдения.

При изучении процессов или явлений методами математической статистики необходимо выделять качественную и количественную стороны процесса или явления. Если качественная сторона характеризует их существенные особенности и основные закономерности, то количественная устанавливает тесноту связи между явлениями, выявляет количественные закономерности и тенденции развития. При этом математико-статистические методы опираются на качественную сторону явления.

Для выявления количественной стороны явления или процесса необходимо располагать статистическими данными. Первым этапом статистического исследования является сбор этих данных, который называют статистическим наблюдением. Результатом такого наблюдения является получение статистической совокупности.

Статистическая совокупность представляет собой множество элементов или единиц одного и того же вида. Применительно к строительству это могут быть совокупности строительных управлений с однородной спецификой работ или осуществляющих строительно-монтажные работы по одному виду строительства; совокупности рабочих одной и той же специальности; совокупности материалов, деталей, конструкций и полуфабрикатов, используемых для получения строительной продукции; совокупности основных производственных фондов строительного назначения и т. д. Таким образом, статистическая совокупность состоит из отдельных элементов. Каждый элемент характеризуется рядом свойств или признаков, которые изменяются под влиянием различных причин или условий, образуя их изменчивость, колеблемость, вариацию.

Статистический материал, полученный в результате статистического наблюдения, подвергается соответствующей обработке или систематизации. Для этого используется метод группировок, который позволяет выявить наиболее типичные черты изучаемого процесса или явления.

Метод группировок предполагает не простое распределение элементов статистической совокупности по отдельным группам, а такое, при котором группы образуются из качественно однородных элементов. Метод группировок позволяет подсчитать количество единиц или элементов статистической совокупности, обладающих конкретным значением определенного признака.

Исходная, или статистическая информация, первоначально представляет собой неупорядоченный ряд результатов отдельных наблюдений. Если эти наблюдения расположить в порядке возрастания или убывания значений признака, то получим ранжированный, или упорядоченный ряд. Подразумевается, что указанный ряд наблюдений образован из элементов генеральной совокупности, отобранных случайным образом и независимо друг от друга.

По ранжированному ряду определяют, сколько раз каждый вариант признака встречается в данной статистической совокупности. В этом случае получается ряд распределения, или вариационный ряд. Отдельные значения признака принято называть вариантами ряда распределения. Элементы статистической совокупности группируются по вариантам признака, при этом для каждой группы определяется число элементов или частота повторения признака. Следовательно, ряд распределения представляет собой таблицу, в которой записаны в определенном порядке варианты того или иного признака и указаны частоты их повторения. Ряды распределения используются для изучения различий между единицами однородной группы по величине какого-либо количественного или качественного признака. Если ряды распределения строятся по количественному признаку, то различают дискретную и непрерывную вариации.

Дискретной вариацией признака называют такую вариацию, у которой отдельные значения признака отличаются друг от друга на некоторую конечную величину или целое число.

Непрерывной вариацией признака называют такую вариацию, при которой отдельные значения признака отличаются друг от друга на сколь угодно малую величину. Примером непрерывной вариации признака может служить процент выполнения плана, производительность труда, время и т. д. Если ряд распределения формируется на основе непрерывного признака, то распределение признака задается по интервалам. В этом случае частоты подсчитываются не по отношению к отдельному значению признака, а по отношению к принятому интервалу. Полученные таким путем ряды распределения называются интервальными вариационными рядами. Однако интервальные ряды распределения могут быть получены и на основе дискретной статистической информации.

Если ряды распределения строятся по качественному признаку (профессия рабочих, вид строительства, вид строительно-монтажных работ и т. д.), то различают атрибутивную вариацию.

Для характеристики вариации признака используют не только абсолютные значения частот, но и относительные величины. В этом случае определяется отношение абсолютной частоты к объему статистической совокупности. Такие величины называются частостью. Они могут выражаться и в процентах.

Интервальные ряды распределения могут иметь равные и неравные интервалы.

Интервальными рядами с равными интервалами называются ряды, в которых все интервалы имеют одну и ту же величину. Интервальные ряды с неравными интервалами имеют различную величину интервала.

Рассмотрим основные правила построения интервальных рядов распределения с равными интервалами, которые получили наибольшее распространение при статистической обработке данных, характеризующих результаты производственно-хозяйственной деятельности строительных организаций.

При построении таких рядов распределения используют метод группировок, суть которого заключается в том, что в результате объединения близких значений признака ряд разбивается на отдельные группы. Первоначально выбирают число интервалов. Оно определяется требованиями наглядности и закономерностями наблюдения: при небольшом количестве наблюдений число интервалов в основном зависит от объема совокупности или числа единиц в ней. При выборе числа интервалов необходимо соблюдать следующие правила: количество интервалов не должно быть очень большим, так как тогда в каждом из них может оказаться недостаточное количество единиц совокупности для выражения отчетливой закономерности; оно не должно быть и очень малым, чтобы сохранить основные качественные признаки ряда распределения. Эмпирическим путем установлено, что при малом числе наблюдений (n≤ 10) вариационный ряд непосредственно используется для дальнейших расчетов.

При большом количестве данных простой вариационный ряд преобразуется в сгруппированный. Данные разбиваются на ряд групп или классов, общее число интервалов k должно быть в пределах 8-25, так как при увеличении k резко возрастает трудоемкость статистических расчетов, а точность результатов не повышается. После выбора числа интервалов приступают к определению его величины. Необходимо стремиться подобрать оптимальную величину интервала, т. е. такую, при которой вариационный ряд не будет слишком громоздким, и будут сохранены особенности данного явления или исследуемого процесса. Для расчета величины интервала используют формулу:

i = R / l (3.25)

где К - размах колебаний признака;

l - число интервалов.

В случае непрерывного признака целесообразно строить гистограмму. Для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого

частичного интервала n_i – сумму частот вариаций, попавших в i-ый интервал.

При графическом изображении интервального ряда распределения по одной из осей координат, а именно по оси абсцисс х, откладывают интервалы значений данного признака, по оси ординат у - абсолютные частоты. Построенная таким образом фигура на осях координат имеет форму прямоугольника и называется гистограммой распределения интервального ряда. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению n_i/h (плотность частоты). Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии n_i/h. Площадь i-го частичного прямоугольника равна (hn_i/h=n_i) сумме частот вариаций i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, то есть объему выборки.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению W_i/h (плотность относительной частоты). Площадь гистограммы относительных частот равна сумме всех относительных частот, то есть единице.

Ордината такого графика есть отношение площади прямоугольника к длине основания, и выражает собой частоту, которая приходится на единицу измерения данного признака. Указанная частота носит название плотности частоты. При наличии интервального ряда с равными интервалами плотность количественно совпадает со значениями абсолютных частот.

Графическое изображение интервального ряда распределения в виде гистограммы показано на рисунке 5а. На нем наглядно представлена выявленная закономерность изменения вариантов данного признака: нарастание частот в левой части графика и постепенное уменьшение их в крайних точках, т. е. данный ряд распределения имеет незначительную правостороннюю асимметрию.

Для систематизации статистического материала в аналитической форме интервальный ряд распределения необходимо представить в виде дискретного ряда распределения, в котором вместо интервалов принимаются их центральные значения.

При построении дискретного ряда распределения абсолютные и относительные частоты остаются без изменения. Дискретные ряды распределения, так же как и интервальные, можно представить в виде графиков. Для графического изображения дискретного ряда распределения по одной из осей координат - оси абсцисс х откладывают центральные значения интервалов, а по оси ординат у - абсолютные частоты. В результате построения получается многоугольник, который носит название полигона распределения. Графическое изображение дискретного ряда распределения дано на рисунке 5б.

а б в

Рисунок 5 –Гистограмма частот (а), полигон частот (б), кривая нормального распределения (в)

Полигоном частот называют ломаную, отрезки которой соединяют точки (X_i; n₁); (X₂; n₂)….(X_k; n_k). Для построения полигона частот на оси абсцисс откладывают варианты X_i, а на оси ординат – соответствующие им частоты n_i. Точки (X_i; n_i) соединяют отрезками прямых и получают полигон частот.

Полигоном относительных частот называют ломанную, отрезки которой соединяют точки (X_i; W₁); (X₂; W₂); (X_k; W_k). Полигон частот дает понятие о том, насколько часто встречается каждое значение [7, 9].

3.2.2 Второй этап – определение точечных оценок распределения

В вероятностных (стохастических системах) наряду с необходимостью действует случайность. Под случайным событием понимается факт, который в результате испытания (осуществления правил) может произойти или не произойти. Мерой объективной возможности случайного события А является вероятность:

Р{A}(0≤ P{A}≤ 1) (3.26)

Случайной величиной Y называется величина, значения которой подвержены некоторому неконтролируемому разбросу при повторении данного процесса (наблюдения, эксперимента). Поведение случайной величины полностью описывается функцией распределения вероятностей F{Y}, которая показывает вероятность того, что случайная величина Y примет значения меньше Y_а:

F{Y}=P{Y≤ Y_a}; (-∞ ≤ Y≤ Y_a) (3.27)

Исчерпывающими вероятностными характеристиками случайной величины являются дифференциальная и интегральная функции распределения. Однако некоторые основные свойства случайных величин могут быть описаны более просто с помощью определенных числовых параметров. Наибольшую роль среди них на практике играют два параметра, характеризующие центр рассеяния (центр распределения) случайной величины и степень ее рассеяния вокруг этого центра. Наиболее распространенной характеристикой центра распределения является математическое ожидание М_х случайной величины Х (часто называемое также генеральным средним значением). Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.

Пусть случайная величина Х может принимать только значения Х₁, Х₂, …Х_n, вероятности которых соответственно равны р₁, р₂, …р_n. Тогда математическое ожидание М(х) случайной величины Х определяется равенством:

М(х) = Х₁р₁ + Х₂р₂ +…+ Х_nр_n. (3.28)

Если дискретная случайная величина Х принимает счетное множество возможных значений, то М(х)=∑ Х_iр_i, (р - вероятность появления значений Х _i). Вероятностный смысл полученного результата таков: математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.

Степень рассеяния случайной величины Х относительно М_Х может быть охарактеризована с помощью генеральной дисперсии S²:

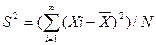
(3.29)

где X_i – выборочная совокупность;

X – среднее значение выборочной совокупности;

N – объем выборочной совокупности.

Если же значения признака Х₁, Х₂, …Х_к имеют соответственно частоты N₁, N₂, …N_k, причем N₁+N₂+…+N_k=N_i, то

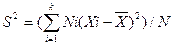(3.30)

где N_i – частоты выборочной совокупности.

то есть генеральная дисперсия есть средняя взвешенная квадратов отклонений и весами, равными соответствующим частотам.

Кроме дисперсии для характеристики рассеяния значений признака генеральной совокупности вокруг своего среднего значения пользуются сводной характеристикой – средним квадратическим отклонением. Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генеральной дисперсии:

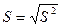(3.31)

где S² – генеральная дисперсия;

S – среднее квадратическое отклонение.

Кроме того, безразмерная характеристика – υ – коэффициент вариации

υ = 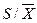(3.32)

Форма кривой распределения характеризуется коэффициентами асимметрии А и коэффициентом островершинности (эксцесс) – Е.

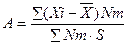(3.33)

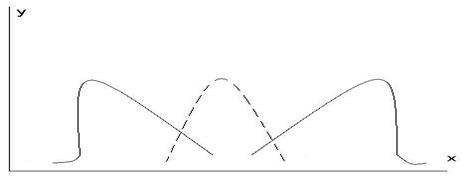
Существует левосторонняя и правосторонняя ассиметрия (рисунок 6).

а б в

Рисунок 6 – Ассиметрия: левосторонняя (а) и правосторонняя (в), б - кривая нормального рапределения

Эксцесс или коэффициент крутости:

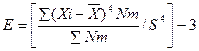(3.34)

Стандартное значение Е = 0; Е < 0 – плосковершинные; Е > 0 – островершинные (рисунок 7).

Две случайные величины называются независимыми, если f(x, y)=f(x)f(y). Как и в одномерном случае, основные свойства двумерной совокупности величин x, y могут быть охарактеризованы с помощью ряда числовых параметров. При этом в качестве наиболее употребительных параметров, описывающих поведение каждой из случайных величин в отдельности, как и выше, применяют математическое ожидание и дисперсия соответствующей случайной величины:

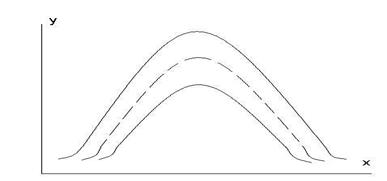
Рисунок 7 – Эксцесс: а – островершинная кривая, б- кривая нормального рапределения, в – плосковершинная кривая

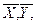S²_x S²_y, S_x S_y. Кроме подобного рода параметров для двумерной совокупности могут быть построены параметры, характеризующие степень взаимозависимости переменных X и Y. Простейшими из них являются ковариация двух случайных величин (называемая также корреляционным моментом) - cov (x, y),

а также нормированный показатель связи – коэффициент корреляции:

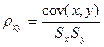(3.35)

По своему физическому смыслу коэффициент корреляции является далеко не исчерпывающей характеристикой статистической связи, характеризуя лишь степень линейной зависимости между X и Y. Коэффициент корреляции меняется в пределах -1≤ 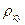≤ 1. Если 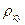=1, то случайные величины полностью положительно коррелированны, то есть y=а₀+а₁х₁, где а₀ и а₁ – постоянные, причем а₁ > 0. Если же 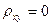, то случайные величины некоррелированны а₁=0. В этом случае, когда Х и Y независимые величины, для них 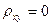, следовательно, они и некоррелированны. Этот коэффициент характеризует наличие или отсутствие линейной функциональной связи. Вычисляется на основе ковариации.

Некоррелированность не следует смешивать с независимостью. Независимые случайные величины всегда некоррелированы. Однако, обратное утверждение неверно: некоррелированные величины могут быть зависимы и даже функционально. Таким образом, коэффициент корреляции характеризует степень приближения зависимости между случайными величинами к линейной функциональной зависимости. Значение коэффициента корреляции определяет насколько зависимость между случайными переменными величинами близка к линейной функциональной зависимости. Коэффициент корреляции часто применяют при определении существования линейной связи между величинами. Если предварительный графический анализ указывает на какую-либо тесноту связи, то полезно вычислить коэффициент корреляции. В том случае, если величина коэффициента корреляции находится в пределах |1….0, 75|, то можно с уверенностью считать, что независимо от вида этой связи, она достаточно тесна для того, чтобы исследовать её форму.

Смысл статистических методов заключается в том, чтобы по выборке ограниченного объема N, то есть по некоторой части генеральной совокупности высказать суждение о ее свойствах в целом. Подобное суждение может быть получено путем оценивания параметров генеральной совокупности с помощью некоторых подходящих функций от результатов наблюдений – оценок.

При многократном извлечении выборок одного и того же объема и последующем нахождении множества оценок одного и того же параметра получатся различные числовые значения этих оценок, изменяющиеся от одной выборки к другой случайным образом. Иными словами, любая оценка произвольного параметра 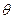есть случайная величина. Сам оцениваемый параметр является неслучайной величиной. Для оценивания одного и того же параметра можно использовать в принципе различные оценки. Чтобы выбрать наилучшую из них, необходимо сформулировать некоторые требования к свойствам оценок, желательные с точки зрения практики.

Основными свойствами оценок являются свойства несмещенности, эффективности и состоятельности. Оценка θ _n параметра θ называется несмещенной, если её математическое ожидание равно оцениваемому параметру θ, то есть

М(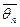) = θ (3.36)

Если это равенство не выполняется, то оценка 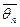может либо завышать значение θ, (то есть М(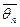)> )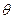, либо занижать его (то есть М(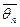)< )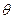. В обоих случаях это приводит к систематическим (одного знака) ошибкам в оценке параметра θ. Требование несмещенности гарантирует отсутствие систематических ошибок при оценке параметров.

Несмещенная оценка 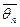, которая имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра θ, вычисленных по выборкам одного и того же объема, называется эффективной оценкой.

Оценка 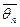параметра θ называется с остоятельной, если она подчиняется закону больших чисел, то есть выполняется следующее равенство:

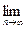{P 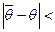ε } = 1 (3.37)

Состоятельность оценки означает, что чем больше объем выборки, тем больше вероятность того, что ошибка оценки не превысит сколь угодно малого положительного числа ε.

Точечные оценки – это оценки некоторых неизвестных числовых параметров распределения. Они представляют собой числа, полученные путем подстановки выборочных значений Х₁, Х₂, …Х_N в формулу для оценивания искомого параметра. Математическое ожидание и дисперсию S² обычно оценивают с помощью следующих соотношений:

М_х= 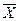= 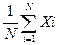(3.38)

S²= 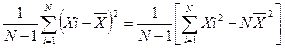(3.39)

Указанные оценки являются состоятельными и несмещенными. Для выборки из нормальной совокупности оценка Х, кроме того, является эффективной.

Если объем выборки не ограничен (N → ∞), то дисперсия параметра S²_x стремится к эффективной или, как говорят, она асимптотически эффективна. Несмещенность оценки S² достигается использованием в знаменателе формулы величины ν = N-1, вместо очевидного на взгляд значения N. Величину ν называют числом степеней свободы. Она равна разности между числом имеющихся экспериментальных значений N, по которым вычисляют оценку дисперсии, и количеством дополнительных параметров, входящих в формулу для оценки этой дисперсии и вычисляемых в виде линейных комбинаций тех же самых наблюдений.

Недостаток точечной оценки, – неизвестно с какой точностью они дают оцениваемый параметр, если для большого числа наблюдений точность обычно бывает достаточной для практических выводов, то для выборок небольшого объема вопрос о точности оценок очень существенен. Поэтому более информа-тивный способ оценивания неизвестных параметров состоит не в определении единичного точечного значения, а в построении интервала, в котором с задан-ной степенью достоверности окажется оцениваемый параметр θ.

3.2.3 Третий этап – определение интервальных оценок, понятие о статистической гипотезе

На этом этапе определяют точечные оценки и доверительные интервалы. В математической статистике рассматриваются не все значения случайной величины х, а только некоторая выборка из этих значений, поэтому среднее значение величины называется не математическим ожиданием, а выборочным средним 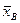. Соответственно вместо дисперсии и среднеквадратического отклонения рассматривают выборочную дисперсию D_в и выборочное среднеквадратическое отклонение. Естественно встает вопрос о точности нахождения 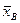, D_в, 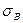, так как она зависит от объема выборки n.

При малых n точность мала, а при n→ ∞ Р_i→ P, 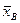→ M_(x), D_в→ D_(x). Это стремление по вероятности, то есть с достаточно большой вероятностью.

Надежностью (доверительной вероятностью) оценки х по найденному х* называют вероятность 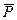, с которой осуществляется неравенство

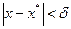(3.40)

т. е. это вероятность того, что х отличается от х* меньше чем на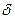

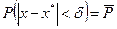(3.41)

Отсюда получаем так называемый доверительный интервал (х* - 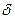, х* + 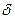), который показывает, что этот интервал заключает в себе (покрывает) неизвестный параметр х с вероятностью, равной .

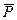Интервальной оценкой параметра θ называется интервал (границы l₁ и l₂), который с заданной вероятностью р накрывает оцениваемый параметр θ:

Р{l₁< θ ≤ l₂} = p (3.42)

Этот интервал называется доверительным, его границы l₁ и l₂, являющиеся случайными величинами – соответственно нижним и верхним доверительным пределами; вероятность – р – доверительной вероятностью. Вычисления обычно начинают с того, что задается их надежность γ, которую принято выбирать равной 0, 95; 0, 99; 0, 999. Тогда вероятность того, что интересующий нас параметр θ не попал в доверительный интервал (θ ₁; θ ₂) не превосходит соответственно 0, 05; 0, 01 или 0, 001. Если мы считаем, что все события вероятность которых меньше 0, 05 (0, 01 или 0, 001), и практически невозможны, то, следовательно, практически достоверно попадание параметра θ в доверительный интервал (θ ₁; θ ₂). Поэтому число (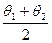) (середина доверительного интервала) будет давать нам значение параметра θ с точностью 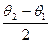и практически достоверно.

Обычно принимают 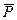= 0, 95 – 0, 97. Исходя из того, что доверительный интервал должен покрывать неизвестный параметр х, по таблицам определяютобъем выборки– n.

Вероятность осуществления неравенства 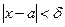для нормально распределенной случайной величины Х находится так (а = M_(x)):

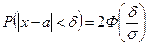(3.43)

где Ф(t) - функция Лапласа;

.

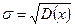Пусть 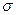известно. Оценим математическое ожидание а по выборочной средней 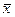при n значениях (объем выборки). Для этого существует оценка

(3.44)

Если задано 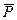, то t находится из равенства 2Ф(t) = 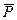по таблице функций Лапласа.

Пусть 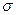=3, n=36, 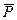=0, 95. Из соотношения 2Ф(t) = 0, 95 по таблице находим t = 1, 96. Следовательно,

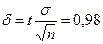(3.45)

Итак, доверительный интервал будет

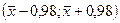(3.46)

Он оказался малым по сравнению с интервалом (а - 3 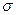, а +3 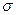), так как 3 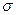= 9.

Если же задано 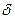, а n нужно определить, то это можно сделать из условия

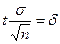(3.47)

Перенос наших знаний от выборочной совокупности к генеральной может быть осуществлен лишь с некоторой вероятностью Р{θ }, т.е суждение о свойствах генеральной совокупности носит вероятностный характер и содержит элемент риска α =1-Р{θ }. Любые суждения о свойствах генеральной совокупности называются статистическими гипотезами (Н). Их проверка осуществляется с помощью статистических критериев (Сr), назначаемых в зависимости от формулировки гипотезы. Все эти критерии отрицательны по своей природе. Если значение изучаемого параметра θ попадает в область “принятия” гипотезы, то это значит лишь, что гипотеза не противоречит экспериментальным (выборочным) данным и её с риском (α =1-Р{θ }) можно признать правомерной (говорят “гипотеза допущена”) по крайней мере до тех пор, пока исследования по расширенной информации или с помощью более мощных критериев не приведут к противоположному результату. Кроме того, неотрицательный результат проверки гипотезы не означает, что она лучшая или единственная (свойством непротиворечивости могут обладать и другие гипотезы), её следует рассматривать лишь как одно из правдоподобных (а не абсолютно достоверных) утверждений.

Основная выдвинутая гипотеза называется нуль-гипотезой (Н₀). Противоречащие ей гипотезы (Н_i) называют альтернативными или конкурирующими. Поскольку проверка гипотез ведется при ограниченной информации (по выборке), то могут возникнуть ошибки двух родов. Если будет отвергнута правильная гипотеза, то совершается ошибка первого рода; если будет допущена неправильная гипотеза, то совершена ошибка второго рода. Все четыре возможные при этом ситуации представлены в таблице 1.

Таблица 1 – Варианты принятия гипотезы

Вероятность допустить ошибку первого рода называется уровнем значимости и обозначается α. Область, отвечающая вероятности α, называется критической, а дополняющая ее область, вероятность попадания в которую Р{θ }=1-α, называется областью естественных (правдоподобных) значений критерия.

Вероятность ошибки второго рода обозначается β, а величина Р{θ }=1-β называется мощностью критерия. Чем больше мощность критерия, тем меньше вероятность совершить ошибку второго рода (однако при этом может возрастать риск α, особенно при малых фиксированных выборках). В работах по контролю качества величина α называется риском производителя (отвергая правильную гипотезу, он бракует годную продукцию), а величина β – риском потребителя (допуская ложную гипотезу, он принимает и использует фактически непригодную продукцию). Выбор значений α и β в таких условиях производится по взаимной договоренности между производителем и потребителем и зависит от технико-экономической тяжести последствий, возникающих от совершения ошибок первого и второго рода.

Если объем выборки n велик (n> 1000), то имеется принципиальная возможность добиваться минимизации ошибок α и β. Если объем фиксированной выборки мал, то обычно задаются уровнем значимости (α), а статистический критерий выбирают так, чтобы минимизировать β.

Чем существеннее потери от ошибочного отклонения гипотезы Н_о, тем меньшей выбирается величина α. Практика исследований в области технологии показывает, что можно ориентироваться на следующие значения α:

- для поисковых рецептурно-технологических задач

α = 5 ÷ 10 %

- для окончательных решений в таких задачах

α = 2 ÷ 5 %

- для задач контроля качества неконструкционных материалов (отделочных, изоляционных и др.)

α = 1 ÷ 5 %

- для задач контроля качества конструкционных материалов и несущих конструкций

α = 0, 1 ÷ 1 %

(меньший предел для случаев, когда нарушение нормальных условий эксплуатации связано с риском для жизни людей).

Чтобы осуществить проверку согласованности теоретических и полученных в эксперименте параметров распределения случайной величины и ее закона распределения, применяют критерии согласия.

Итак, на основании данного статистического материала нам предстоит проверить гипотезу Н, состоящую в том, что случайная величина х подчиняется некоторому определенному закону распределения. Для того, чтобы принять или опровергнуть гипотезу Н, рассматривается некоторая величина И, характеризующая степень расхождения теоретического и статистического распределения. Эта величина будет случайной величиной. Закон распределения этой случайной величины зависит от закона распределения случайной величины х, над которой производились опыты, и от числа опытов n. Если гипотеза Н верна, то закон распределения величины И определится законом распределения величины х и числом n. Допустим, что этот закон распределения известен, и в результате данной серии опытов найдено конкретное значение меры расхождения И, т. е. 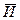. для ответа на вопрос о верности гипотезы Н вычислим вероятность того, что за счет случайных причин мера расхождения И окажется не меньше 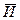. Если эта вероятность мала, то гипотезу Н следует отвергнуть как мало вероятную. Если эта вероятность значительна, следует признать, что экспериментальные данные не противоречат гипотезе Н.

Оказывается, что при некоторых способах выбора меры И закон распределения величины И обладает весьма простыми свойствами и при достаточно больших n практически не зависит от закона распределения величины х. Именно такими мерами расхождения и пользуются в математической статистике в качестве критериев согласия.

Наиболее часто применяемые критерии согласия: критерий 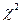Пирсона, критерий Кохрена, критерий Фишера и др. для этих критериев составлены таблицы значений вероятности Р(И ≤ 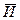). В зависимости от 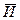числа степеней свободы k, которое характеризуется числом опытов n и числом наложенных связей s (k = n - s).

В качестве практического использования критериев согласия рассмотрим задачу сравнения нескольких дисперсий нормальных генеральных совокупностей по выборкам одинакового объема по критерию Кохрена.

Пусть генеральные совокупности Х₁, Х₂,..., Х_I распределены нормально. Из этих совокупностей извлечено l выборок одинакового объема n и по ним найдены исправленные выборочные дисперсии 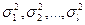, все с одинаковым числом степеней свободы k = n - 1 (выборочной дисперсией называют среднее арифметическое квадратов отклонений наблюдаемых значений признака от их среднего значения)

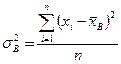(3.48)

Исправленная выборочная дисперсия (ближе к генеральным дисперсиям) вычисляется по формуле

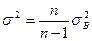(3.49)

Требуется по исправленным дисперсиям при заданном уровне значимости α (при рассмотрении доверительного интервала доверительная вероятность бралась 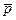= 0, 95, а уровень значимости α = 1 - 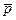= 0, 05) проверить нулевую гипотезу (основную гипотезу), состоящую в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой

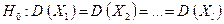(3.50)

Другими словами, требуется проверить, значимо или незначимо различаются исправленные выборочные дисперсии.

Можно применить для этого критерий Фишера, критерий Бартлета, но предпочтительнее использование критерия Кохрена, распределение которого найдено точно.

Критерий Кохрена - это отношение максимальной исправленной дисперсии к сумме всех исправленных дисперсий

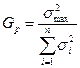(3.51)

Распределение этой случайной величины зависит только от числа степеней свободы k = n - 1 и количества выборок l.

Находят критическую точку G (α, k, l) по таблице. Если 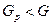, нет основания отвергать нулевую гипотезу, если 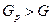, то нулевую гипотезу отвергают.

Рассмотрим на конкретном примере. По четырем независимым выборкам одинакового объема n = 17, извлеченным из нормальных генеральных совокупностей, найдены исправленные дисперсии: 0, 26; 0, 36; 0, 40; 0, 42. Требуется при уровне значимости 0, 05 проверить нулевую гипотезу об однородности генеральной дисперсии и оценить генеральную дисперсию.

Найдем значение критерия Кохрена

.

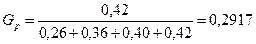Найдем по таблице по уровню значимости α = 0, 05, числу степеней свободы k = 17 - 1 = 16 и числу выборок l = 4 критическую точку

G (0, 05; 16; 4) = 0, 4366.

Так как 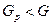, нет оснований отвергать нулевую гипотезу об однородности дисперсий, т. е. использованные выборочные дисперсии различаются незначимо.

Поскольку нулевая гипотеза справедлива, в качестве оценки генеральной дисперсии примем среднюю арифметическую исправленных дисперсий

.

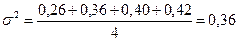Рассмотрим проверку гипотезы о значимости выборочного коэффициента корреляции.Пусть двумерная генеральная совокупность (X, Y) распределена нормально. Из этой совокупности извлечена выборка объемом n, и по ней найден выборочный коэффициент корреляции r_в, который оказался отличным от нуля. Так как выборка отобрана случайно, то еще нельзя заключить, что коэффициент корреляции генеральной совокупности r_г также отличен от нуля. Так как нас интересует именно этот коэффициент, то возникает необходимость при за