
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нормальный закон распределения случайных величин
|
|
Нормальный закон распределения(закон Гаусса) играет исключительно важную роль в теории вероятностей. Во-первых, это наиболее часто встречающийся на практике закон распределения непрерывных случайных величин. Во-вторых, он являетсяпредельным законом в том смысле, что к нему при определенных условиях приближаются другие законы распределения.
Нормальный закон распределения характеризуется следующей формулой для плотности вероятности:
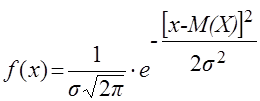 , (26)
, (26)
где х – текущие значения случайной величины X; М (X) и s – ее математическое ожидание и стандартное отклонение. Из (26) видно, что если случайная величина распределена по нормальному закону, то достаточно знать только два числовых параметра: М (Х) и s, чтобы полностью знать закон ее распределения.
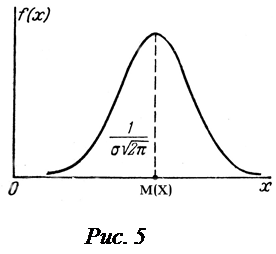 График функции (26) называется нормальной кривой распределения (кривой Гаусса). Он имеет симметричный вид относительно ординаты х = М (Х). Максимальная плотность вероятности, равная
График функции (26) называется нормальной кривой распределения (кривой Гаусса). Он имеет симметричный вид относительно ординаты х = М (Х). Максимальная плотность вероятности, равная 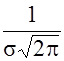 »
»  , соответствует математическому ожиданию М (Х) =
, соответствует математическому ожиданию М (Х) = 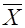 ; по мере удаления от нее плотность вероятности f (х) падает и постепенно приближается к нулю (рис. 5).
; по мере удаления от нее плотность вероятности f (х) падает и постепенно приближается к нулю (рис. 5).
Величина М (Х) называется также центром рассеяния. Среднеквадратичное отклонение s характеризует ширину кривой распределения.
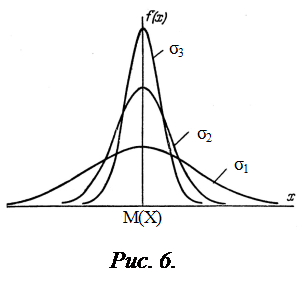 При изменении значения М (Х) в (26) нормальная кривая не меняется по форме, но сдвигается вдоль оси абсцисс. С возрастанием s максимальная ордината кривой убывает, а сама кривая, становясь более пологой, растягивается вдоль оси абсцисс, при уменьшении sкривая вытягивается вверх, одновременно сжимаясь с боков. Вид кривой распределения при разных значениях s: (s3< s2< s1) показан на рис.6.
При изменении значения М (Х) в (26) нормальная кривая не меняется по форме, но сдвигается вдоль оси абсцисс. С возрастанием s максимальная ордината кривой убывает, а сама кривая, становясь более пологой, растягивается вдоль оси абсцисс, при уменьшении sкривая вытягивается вверх, одновременно сжимаясь с боков. Вид кривой распределения при разных значениях s: (s3< s2< s1) показан на рис.6.
Естественно, что при любых значениях М (Х) и s площадь, ограниченная нормальной кривой и осью Х, остается равной 1 (условие нормировки):
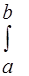 f (х) dх = 1, или
f (х) dх = 1, или 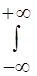 f (х) dх = 1.
f (х) dх = 1.
Нормальное распределение симметрично, поэтому
М (Х) = Мо (Х) = Ме (Х).
Вероятность попадания значений случайной величины Х в интервал (x 1, x 2), т.е. Р (x 1 < Х< x 2), равна:
Р (x1 < Х < x2) = 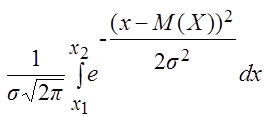 . (27)
. (27)
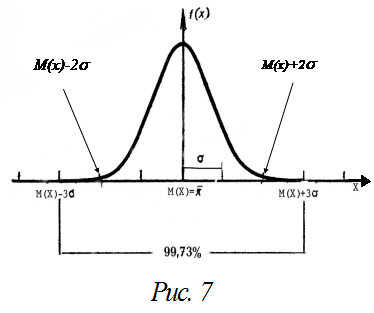 На практике часто приходиться вычислять вероятности попадания значений нормально распределенной случайной величины на участки, симметричные относительно М (Х). В частности, рассмотрим следующую, важную в прикладном отношении задачу. Отложим от М (Х) вправо и влево отрезки, равные s, 2s и 3s (рис. 7) и проанализируем результат вычисления вероятности попадания Х в соответствующие интервалы:
На практике часто приходиться вычислять вероятности попадания значений нормально распределенной случайной величины на участки, симметричные относительно М (Х). В частности, рассмотрим следующую, важную в прикладном отношении задачу. Отложим от М (Х) вправо и влево отрезки, равные s, 2s и 3s (рис. 7) и проанализируем результат вычисления вероятности попадания Х в соответствующие интервалы:
Р (М (Х) – s < Х< М (Х) + s) = 0, 6827 = 68, 27 %. (28)
Р (М (Х) – 2s < Х< М (Х)+ 2s) = 0, 9545 = 95, 45 %. (29)
Р (М (Х) –3s < Х< М (Х) + 3s) = 0, 9973 = 99, 73 %. (30)
Из (30) следует: практически достоверно, что значения нормально распределенной случайной величины Х с параметрами М (Х) и s лежат в интервале М (Х) ± 3s. Иначе говоря, зная М (Х) = 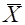 и s, можно указать интервал, в который с вероятностью Р = 99, 73% попадают значения данной случайной величины. Такой способ оценки диапазона возможных значений Х известен как «правило трех сигм».
и s, можно указать интервал, в который с вероятностью Р = 99, 73% попадают значения данной случайной величины. Такой способ оценки диапазона возможных значений Х известен как «правило трех сигм».
Пример. Известно, что для здорового человека р Н крови является нормально распределенной величиной со средним значением (математическим ожиданием) 7, 4 и стандартным отклонением 0, 2. Определите диапазон значений этого параметра.
Решение: для ответа на этот вопрос воспользуемся “правилом трех сигм”. С вероятностью равной 99, 73% можно утверждать, что диапазон значений р Н для здорового человека составляет 6, 8 – 8.
Задачи
1. Задают ли законы распределения дискретной случайной величины следующие таблицы?
1) 2)
| Х | Х | |||||||||
| Р | 0, 1 | 0, 4 | 0, 3 | 0, 2 | Р | 0, 1 | 0, 2 | 0, 3 | 0, 5 |
Ответ: закон распределения задает только первая таблица
2. Дискретная случайная величина Х имеет закон распределения:
| Х | |||||
| Р | Р 1 | 0, 15 | Р 3 | 0, 25 | 0, 35 |
1) Найдите вероятность р 1= Р (Х =3) и р 3= Р (Х =5), если известно, что р 3 в 4 раза больше р 1..
2) Получив ответ на первый вопрос, постройте многоугольник распределения.
Ответ: р 1=0, 05; р 3=0, 2
3. Плотность распределения случайной величины Х задана функцией
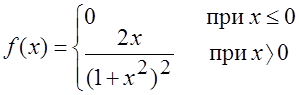
Найдите вероятность того, что значение случайной величины Х принадлежит интервалу (2, 3).
Ответ: 0, 2
4.
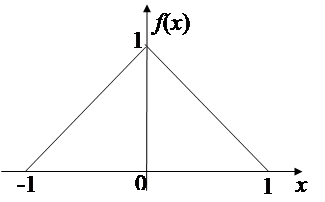 |
График плотности распределения вероятностей случайной величины Х изображен на показанном ниже рисунке.
Запишите аналитическое выражение для плотности вероятностей.
Ответ: f (x) = 0 при | x | > 1
f (x) = x +1 при –1< x ≤ 0
f (x) = - x +1 при 0< x ≤ 1)
5. Найдите математическое ожидание дискретной случайной величины, закон распределения которой задан таблицей
| Х | |||||
| Р | 0, 1 | 0, 2 | 0, 4 | 0, 2 | 0, 1 |
Ответ: 5
6. Плотность распределения вероятностей случайной величины Х задана функцией:
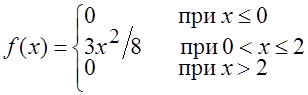
Найдите математическое ожидание случайной величины Х.
Ответ: 1, 5.
7. Длительность жизненного цикла (в днях) для некоторого растения является случайной величиной Х с функцией плотности вероятности f(x) = 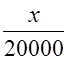 при 0≤ х ≤ 200 и f (х) = 0 при любых других значениях х. Определите среднюю длительность жизненного цикла у этого растения.
при 0≤ х ≤ 200 и f (х) = 0 при любых других значениях х. Определите среднюю длительность жизненного цикла у этого растения.
Ответ: 133, 3 дня.
8. Дискретная величина Х имеет закон распределения:
| Х | 0, 4 | 0, 6 | 0, 8 | ||
| Р | 0, 1 | 0, 2 | 0, 4 | Р4 | 0, 1 |
Чему равна вероятность р 4?
Найдите математическое ожидание, дисперсию, стандартное отклонение и моду этой случайной величины.
Ответ: р 4=0, 24; М (Х)=0, 58; D (X)=0, 068; s(Х)=0, 26; Мо =0, 6).
9. Экспериментальная операция длится не менее 4 мин., но для ее завершения никогда не требуется более 10 мин. Определим случайную величину Т как время, необходимое для выполнения операции и допустим, что функция плотности вероятности для Т имеет вид: f (t) = k (t –4) × (10 – t) на интервале 4 £ t £ 10. Найдите значение постоянной k для этой f (t).
Ответ: 1/36.
10. Найдите числовые характеристики М (Х), D (Х), s(Х) непрерывной случайной величины Х, заданной плотностью вероятности:
f (х) = 
Ответ: М (Х) = 2/3; D (Х) = 1/18; s(Х)» 0, 24.
11. Запишите плотность распределения для случайной величины Х, распределенной по нормальному закону, если М (Х) = 3, D (Х) = 4.
Ответ: 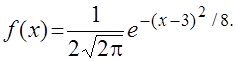
12. Случайная величина Х распределена нормально с математическим ожиданием М (Х) = 10. Вероятность попадания Х в интервал (10, 20) равна 0, 3. Чему равна вероятность попадания Х в интервал (0, 10)?
Ответ: 0, 3.
13. Длина интервала, симметричного относительно математического ожидания, в который с вероятностью 0, 9973 попадают значения некоторой случайной величины, распределенной нормально, равна 30 ед. длины. Найдите стандартное отклонение.
Ответ: 5 ед. длины.
14. Диастолическое давления крови у женщин, страдающих гипертонической болезнью, в среднем равно 95 мм рт. ст., стандартное отклонение – 15 мм рт.ст. Определите интервал возможных значений этой величины, считая, что она распределена по нормальному закону.
Ответ: (50 – 140)мм рт.ст.
15. Считая, что случайная величина Х – диаметр лекарственной таблетки – распределена по нормальному закону с параметрами 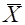 = 10 мм, s= 0, 1 мм, найдите интервал, в котором с вероятностью 95, 45 % будут заключены эти диаметры. Если в партии 3000 таблеток, то сколько из них окажется в этом интервале?
= 10 мм, s= 0, 1 мм, найдите интервал, в котором с вероятностью 95, 45 % будут заключены эти диаметры. Если в партии 3000 таблеток, то сколько из них окажется в этом интервале?
Ответ: (9, 8 – 10, 2)мм; 2864 табл.
* В этом случае считают, что значения некоторой случайной величины Х могут лежать в интервале (-¥; ¥), т.е. на всей числовой оси.
* Обычно случайные величины обозначают прописными буквами латинского алфавита, а их возможное значение и вероятности этих значений – строчными.
* Приведем пример, поясняющий этот факт. Пусть случайная величина – уровень осадков, выпавших за год. Она может принимать любые значения из некоторого интервала. Однако, вероятность того, что в заданный год этот уровень окажется точно равен 40 см, фактически равна 0.
** Иногда рассматривают интервал (– ¥; + ¥)
|
|