Марковский процесс с дискретным множеством состояний и дискретным временем (цепь Маркова с дискретным временем)

Важнейшими вероятностными характеристиками этого процесса являются вероятность перехода 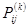системы из состояния 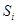на 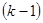шаге в состояние 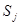на k шаге (переход за один шаг) и вероятность 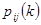того, что за k шагов система перешла из начального состояния 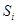в состояние .

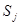Марковское свойство процесса выражается в том, что вероятность 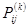зависит лишь от состояния 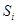, в которое попала система на 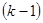шаге, и не зависит от того, как и когда система пришла в это состояние.

Если вероятности 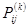не зависят от номера шага, то цепь Маркова называется простой (или однородной): 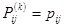, 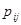– вероятность перехода системы за один шаг из состояния 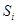в состояние .

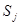Рассмотрим простую цепь Маркова в системе с конечным множеством состояний: 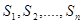. Матрица 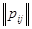, составленная из переходных вероятностей 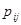, называется матрицей перехода за один шаг.

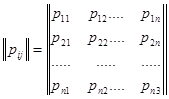, (1)

а матрица

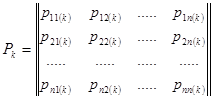. (2)

матрицей перехода системы за k шагов.

Очевидно,

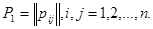
Зная матрицу 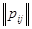, можно найти вероятности 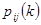с помощью равенства Маркова

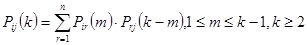(3)

или в матричной форме

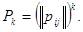(4)

Пример 1 Задана матрица 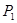вероятностей перехода цепи Маркова из состояния 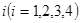в состояние 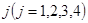и известно начальное состояние системы:

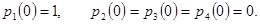
Найти вероятности состояний системы после третьего шага.

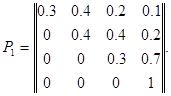
Решение. Вероятности состояний системы на первом шаге есть переходные вероятности, стоящие в первой строке матрицы 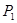, так как по условию задачи в начальный момент времени система находилась в состоянии :

, , , .

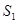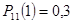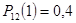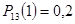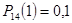Для расчета вероятностей состояний на втором шаге используем равенство Маркова (3)

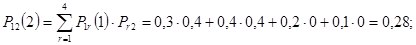
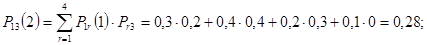
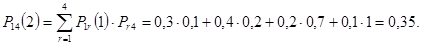
Вероятности состояний системы на втором шаге можно найти также после построения матрицы :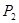

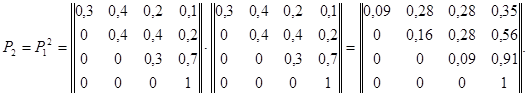
В первой строке этой матрицы стоят вероятности состояний на втором шаге. Если бы в начальный момент времени система находилась, например, в третьем состоянии

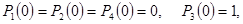
то третья строка матрицы 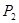дала бы вероятности состояний системы на втором шаге:

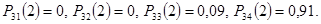
Выводы. Вероятности состояний после третьего шага можно найти по формуле (3) или построив матрицу :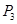

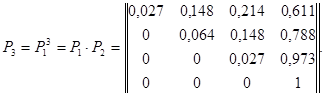
В первой строке этой матрицы стоят вероятности состояний после третьего шага, если в начальный момент времени система была в состоянии :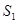

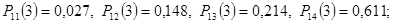
остальные элементы матрицы дают

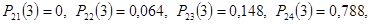
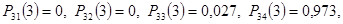
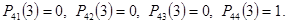
ВАРИАНТЫ К ТИПОВОМУ РАСЧЕТУ