
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Классификация состояний цепи Маркова с дискретным временем
|
|
Определение. Состояние i Î X цепи Маркова называется несущественным, если
$ m, j 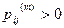 ,
, 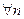
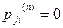 ,
,
то есть существует такое состояние j, в которое можно попасть с положительной вероятностью, но из которого нельзя вернуться в i. Здесь pij(m ) - вероятность перехода цепи Маркова из состояния i в состояние j за m шагов.
Если из множества X выделить все несущественные состояния, то оставшееся множество существенных состояний обладает тем свойством, что, попав в него, цепь Маркова никогда из него не выйдет.
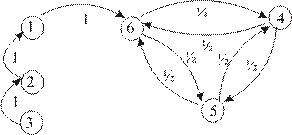
Рис. 1.
Как видно из рисунка, {1, 2, 3} – несущественные состояния, {4, 5, 6} – существенные.
Рассмотрим множество существенных состояний.
Определение. Состояние j называется достижимым из состояния i (обозначается i®j), если $ n> 0, что pij(n )> 0.
Определение. Состояния i и j называются сообщающимися (обозначается i «j), если j достижимо из i, и i достижимо из j.
По определению отношение ««» является симметричным (i «j Þ j «i), и нетрудно убедиться, что оно транзитивно (i «j, j «k Þ i «j).
Множество существенных состояний можно разбить на конечное или счетное число непересекающихся множеств X1, X2, …, состоящих из сообщающихся состояний и характеризующихся тем, что переходы между различными множествами невозможны.
Определение. Множества X1, X2, … называются замкнутыми классами, или неразложимыми классами, существенных сообщающихся состояний. Цепь Маркова, состояния которой образуют один неразложимый класс, называется неразложимой.
Пример 2.2. Классифицировать состояния цепи Маркова с множеством состояний X={1, 2, 3, 4, 5} и матрицей вероятностей переходов
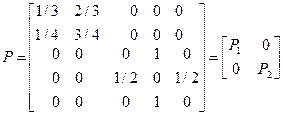 .
.
Решение: Граф вероятностей переходов имеет вид

Очевидно, что у рассматриваемой цепи все состояния существенные и есть два неразложимых класса X1={1, 2}, X2={3, 4, 5}, и исследование ее свойств сводится к исследованию свойств каждой из двух цепей с матрицами вероятностей переходов соответственно P 1 и P 2.
Проведенная классификация позволяет привести матрицу вероятностей переходов к каноническому виду. Для этого выделяют неразложимые классы, а также отдельно несущественные состояния. Тогда матрица P примет вид
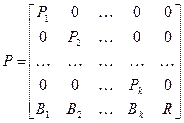 ,
,
где Ps – матрица вероятностей переходов s -го неразложимого класса, 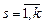 ; Bs – матрица вероятностей переходов из несущественных состояний в состояние s -го замкнутого класса; R – матрица вероятностей переходов по несущественным состояниям.
; Bs – матрица вероятностей переходов из несущественных состояний в состояние s -го замкнутого класса; R – матрица вероятностей переходов по несущественным состояниям.
Пример 2.3. Классифицировать состояния цепи Маркова, заданной матрицей вероятностей переходов за один шаг.
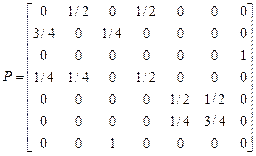 .
.
Решение: Граф переходов для данной цепи Маркова имеет вид

Рис. 2.
Очевидно, что у рассматриваемой цепи состояния 1, 4, 2 – несущественные, 3, 5, 6, 7 –существенные, кроме того, есть два неразложимых класса X1={3, 7} X2={5, 6}. Следовательно, канонический вид матрицы вероятностей переходов следующий:
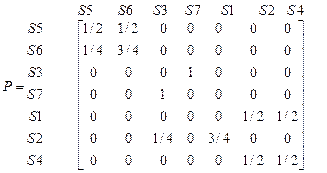 .
.
Пример 2.4. Рассмотрим теперь неразложимый класс, изображенный на рис.3
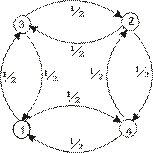
Рис. 3.
Решение: Заметим, что здесь возвращение в каждое состояние возможно лишь за четное число шагов, переход в соседнее состояние – за нечетное число шагов, а матрица вероятностей переходов имеет блочную структуру:
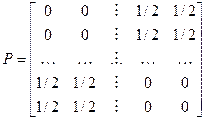 .
.
Отсюда видно, что класс Xs={1, 2, 3, 4} разбивается на два подкласса C0={1, 2} иC1={3, 4}, обладающих следующим свойством цикличности: за один шаг цепь Маркова из C0 непременно переходит в C1, а из C1 – в C0, но за два шага возвращается в исходный класс.
Этот пример показывает возможность разбиения неразложимых классов на циклические подклассы.
Определение. Будем говорить, что состояние j замкнутого класса имеет период d (j), если d (j) есть наибольший общий делитель чисел n таких, что pjj (n)> 0.
Очевидно, что для предыдущего примера (рис. 3) d (j)=2, для всех j.
Определение. Если d (j)=1, (d (X)=1), то состояние j (класс X) называется апериодическим (эргодическим).
|
|