
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Эргодические случайные процессы
|
|
Для стационарных случайных процессов кроме средних статистических характеристик вводятся ещё характеристики, средние по времени.
Выберем 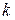 -ю реализацию – x( k )(t) случайного процесса и будем наблюдать её в течение времени 2 T. Рассмотрим среднее по времени значение этой реализации
-ю реализацию – x( k )(t) случайного процесса и будем наблюдать её в течение времени 2 T. Рассмотрим среднее по времени значение этой реализации
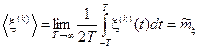 .
.
Здесь символ á ñ обозначает усреднение по времени, в отличие от символа математического ожидания M – усреднения по распределению, или статистического усреднения. Это среднее по времени можно рассматривать как постоянную составляющую случайного процесса x(t). Аналогично можно определить усреднённую по времени функцию корреляции для стационарного процесса
 .
.
Заметим, что не для любого стационарного случайного процесса, приведённые средние по времени характеристики имеют конечные значения. Но даже если такие характеристики существуют, то они могут быть различны для разных реализаций случайного процесса. Исключение составляют эргодические процессы, для которых эти характеристики одинаковы для всех реализаций и, кроме того, совпадают с соответствующими статистическими средними.
Определение. Случайный процесс будем называть эргодическим, если любая его статистическая характеристика, равна соответствующей характеристики, полученной усреднением по времени одной единственной реализации.
Из эквивалентности двух способов усреднения эргодического случайного процесса по распределению и по времени следует, что нет необходимости изучать свойства всего ансамбля реализаций, но достаточно одной реализации для определения всех характеристик рассматриваемого процесса.
Необходимыми и достаточными условиями эргодичности случайного процесса являются: строгая стационарность и, так называемая, метрическая транзитивность, состоящая в том, что любая часть ансамбля реализаций случайного процесса, вероятностная мера которого отлична от 0 или 1, уже не является строго стационарным случайным процессом.
Рассмотрим пример строго стационарного, но неэргодического процесса. Пусть x(t)=h(t)+z, где h(t) – эргодический случайный процесс, а z – некоторая случайная величина. Очевидно, процесс x(t) является строго стационарным, но его средние по времени характеристики различны для различных реализаций, поэтому такой случайный процесс будет неэргодическим.
Итак, если случайный процесс эргодический, то любая его реализация определяет свойства всего ансамбля и поэтому результат усреднения по времени, выполненный по одной реализации, совпадает с соответствующей статистической характеристикой процесса, то есть
 ,
,
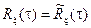 .
.
Можно ввести и другие средние по времени характеристики эргодического процесса. Так, среднее время пребывания процесса ниже уровня x совпадает с вероятностью того, что значения случайного процесса в любой момент времени меньше, чем x, то есть
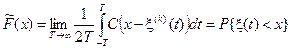 ,
,
здесь
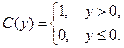
Одномерная характеристическая функция определяется как среднее по времени значение процесса exp{ix( k )(t) u }, то есть в виде
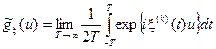 .
.
Основное преимущество средних по времени характеристик состоит в том, что для их вычисления требуется наблюдение за одной единственной реализацией, чем чаще всего и располагает исследователь.
Задачи для самостоятельного решения
1. Случайный процесс x(t) принимает два значения +1 и –1. Число перемен знаков за время t подчиняется распределению Пуассона с параметром m. В начальный момент времени оба значения равновероятны. Найти математическое ожидание, дисперсию и функцию корреляции этого процесса и определить является ли этот процесс стационарным.
2. Случайный процесс x(t) состоит из горизонтальных отрезков единичной длины, ординаты которых независимые случайные величины с плотностью 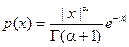 . Найти математическое ожидание, дисперсию и функцию корреляции процесса x(t). Определить, является ли данный процесс стационарным, по крайней мере, в широком смысле.
. Найти математическое ожидание, дисперсию и функцию корреляции процесса x(t). Определить, является ли данный процесс стационарным, по крайней мере, в широком смысле.
3. U и V независимые случайные величины, равномерно распределенные в интервале [ a, b ] и [ c, d ] соответственно. Найти математическое ожидание, дисперсию и функцию корреляции процесса S (t)= U+Vt. Является ли этот процесс стационарным?
4. Случайный процесс задан в виде x(t)= U cos at + V sin at, где a – неслучайная величина, U и V – некоррелированные случайные величины, равномерно распределенные в интервале [–1, 1] и [–2, 2] соответственно. Найти математическое ожидание, дисперсию и функцию корреляции данного процесса. Является ли данный процесс стационарным?
5. Найти функцию ковариации процесса виде h(t)=x(t)cos(Bt +f),, где B – неслучайная величина, x(t) – стационарный случайный процесс с математическим ожиданием m и функцией ковариации K(t), f – случайная величина, равномерно распределенная на отрезке [0, 2p], x(t) и f независимые. Является ли этот процесс стационарным?
6. Найти функцию взаимной ковариации процесса и его второй производной, если процесс x(t) имеет математическое ожидание равное a t и функцию ковариации Kx(t, s)= e -( t+s ).
7. Пусть h1(t) и h2(t) – независимые случайные процессы с корреляционными функциями R 1(t, s) и R 2(t, s), соответственно. Найти корреляционную функцию процесса x(t)= h1(t)h2(t).
8. Найти математическое ожидание, дисперсию и функцию корреляции случайного процесса h(t)= X cos(t + Y), где X имеет нормальное распределение с нулевым математическим ожиданием и единичной дисперсией, Y – случайная величина, равномерно распределенная на отрезке [0, 2p].
9. Пусть h – нормальная случайная величина с функцией распределения 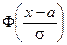 . Найти двумерное распределение случайного процесса x(t)=h+t, где tÎ R.
. Найти двумерное распределение случайного процесса x(t)=h+t, где tÎ R.
10. U и V – независимые случайные величины, распределенные по экспоненциальному закону с параметрами l1 и l2, соответственно. Найти математическое ожидание, дисперсию и функцию корреляции процесса S (t)= U+Vt. Является ли этот процесс стационарным?
11. Случайный процесс S (t)= Ue-at+Ve-bt, где U и V – некоррелированные случайные величины с нулевым математическим ожидание, a и b неслучайные величины. Найти математическое ожидание, дисперсию и функцию корреляции процесса x(t). Определить, является ли данный процесс стационарным, по крайней мере, в широком смысле.
12. Случайный процесс S (t)= t+Ue-at+Ve-bt, где U и V – некоррелированные случайные величины с нулевым математическим ожидание и дисперсиями D 1 =D 2 = 2, a и b неслучайные величины. Найти математическое ожидание, дисперсию и функцию корреляции процесса x(t). Определить, является ли данный процесс стационарным, в широком смысле.
13. Случайная величина x распределена равномерно в интервале [0, 2p]. Для случайного процесса h(t)=x t + a, где a – неслучайная величина, найти математическое ожидание, дисперсию и функцию корреляции. Является ли этот процесс стационарным?
14. Случайный процесс задан в виде x(t)= Vt 2, где V – непрерывная случайная величина, распределенная по нормальному закону с параметрами a и s2. Найти вероятностные характеристики процесса x(t) (математическое ожидание, дисперсию и функцию корреляции). Проверить является ли этот процесс стационарным в широком смысле?
15. Доказать строгую стационарность процесса x(t)= a cos(b t +j), где a, b – неслучайные величины, j –случайная величина равномерно распределенная на отрезке [0, 2p].
16. Случайный процесс представляет собой x(t)= V, где V– непрерывная случайная величина с плотностью pv (x). Найти вероятностные характеристики процесса x(t) (математическое ожидание, дисперсию и функцию корреляции). Является ли этот процесс стационарным?
17. Поток покупателей является простейшим Пуассоновским с параметром l, это значит, что вероятность того, что за время t появится ровно k покупателей определяется формулой Пуассона
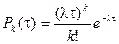 ,
,
Процесс x(t) представляет собой число покупателей пришедших от 0 до t (например, совпадает с началом рабочего дня). Найти математическое ожидание, дисперсию и функцию корреляции процесса x(t). Указание. При вычислении функции корреляции воспользоваться тем, что при s > t x(s)= x(t)+Dx, где Dx – число событий наступивших за время от t до s.
18. Пусть x – случайная величина, имеющая нормальное распределение с математическим ожиданием m и дисперсией s2. Найти функцию корреляции случайного процесса h(t)=x2 t + b, где b – вещественное число, t> 0.
19. Имеется пуассоновский поток случайных событий с интенсивностью l. Случайный процесс x(t) образуется следующим образом: в момент времени i -го события (i =1, 2…) процесс принимает случайное значение Vi и сохраняет его до появления следующего события в потоке. В начальный момент времени x(0)= V 0. Случайные величины V 0, V 1, …– независимы и одинаково распределены с плотностью pV (x). Найти основные характеристики процесса.
20. Найти корреляционную функцию случайного процесса 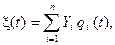 где q 1(t), q 2(t), …, q n(t) – неслучайные функции, Y 1, Y 2, …Yn – некоррелированные случайные величины математическими ожиданиями m 1, m 2, …, mn и дисперсиями d 1, d 2, …, dn соответственно.
где q 1(t), q 2(t), …, q n(t) – неслучайные функции, Y 1, Y 2, …Yn – некоррелированные случайные величины математическими ожиданиями m 1, m 2, …, mn и дисперсиями d 1, d 2, …, dn соответственно.
21. Пусть R (t, s) – корреляционная функция некоторого случайного процесса, Q(z) – полином с положительными коэффициентами. Доказать, что функция R (t, s)= Q (R (t, s)) является корреляционной функцией некоторого случайного процесса.
22. Пусть X~ N (m, s), b – вещественное число. Найти функцию корреляции СП случайного процесса Y (t)= Xt+b, t> 0.
23. Случайный процесс X (t) имеет вид X (t)= U+Vt, где U и V – независимые случайные величины, равномерно распределенные на отрезке [0, 1], 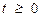 . Вычислить вероятность P(A) случайного события
. Вычислить вероятность P(A) случайного события
 .
.
24. Пусть X и Y – независимые одинаково распределенные случайные величины, принимающие значения –1 и +1 с вероятностями 1/2. Исследовать на стационарность случайный процессx(t)= X cos lt + Y sinl t, t³ 0.
25. Пусть X (t), t³ 0 – пуассоновский случайный процессс параметром l. Доказать, что случайный процесс Y (t)= X (t+ 1)- X (t), t³ 1 является стационарным в широком смысле.
26. Является ли стационарной последовательность попарно независимых одинаково распределенных случайных величин?
27. Пусть j(t)– непрерывная периодическая функция с периодом T, X – случайная величина, равномерно распределенная на отрезке [0, T]. Исследовать случайный процесс Y (t)= j (t+X) на стационарность.
28. Доказать, что сумма независимых стационарных случайных процессов является стационарным случайным процессом.
29. Найти функцию ковариации процесса x(t)= X cos(t + Y), где X, Y независимы, X имеет нормальное распределение N (0; 1), а Y имеет равномерное распределение на [-p; p].
30. Пусть X (t) – стационарный случайный процесс, Y – случайная величина. Является ли случайный процесс Z (t)= X (t)+ Y стационарным?
31. Показать, что функция 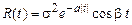 , где
, где  – некоторые положительные постоянные, может быть функцией корреляции непрерывного в среднем квадратическом и стационарного в широком смысле случайного процесса. Определить спектральную плотность, соответствующую такой функции корреляции.
– некоторые положительные постоянные, может быть функцией корреляции непрерывного в среднем квадратическом и стационарного в широком смысле случайного процесса. Определить спектральную плотность, соответствующую такой функции корреляции.
32. Случайный процесс X (t) имеет вид 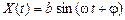 , где b, w – известные числа, j – случайная величина с плотностью распределения вероятностей f (x), t ³ 0. Исследовать случайный процесс X (t) на стационарность и на эргодичность в следующих случаях:
, где b, w – известные числа, j – случайная величина с плотностью распределения вероятностей f (x), t ³ 0. Исследовать случайный процесс X (t) на стационарность и на эргодичность в следующих случаях:
a) f (x) = cos х при х Î [0, p/2];
б) f (x) = 1/2p при x Î [0, 2p], f (x) = 0 при x Ï [0, 2p].
33. Случайный процесс x(t) задан четырьмя равновероятными реализациями:
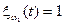 ;
; 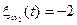 ;
;
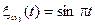 ;
; 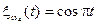 .
.
Найти вероятностные характеристики процесса x(t) (математическое ожидание, дисперсию и функцию корреляции). Является ли этот процесс стационарным, по крайней мере в широком смысле
|
|