Линейная регрессия. Важный случай регрессии первого порядка называется парной линейной регрессией

Важный случай регрессии первого порядка 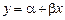называется парной линейной регрессией. Этот вид зависимости часто встречается в практических расчетах.

Так, если об изучаемом явлении нет никаких косвенных сведений, кроме наблюдений, проводимых в настоящий момент, то предварительный характер зависимости можно выяснить, нанося данные в виде точек на координатной плоскости, причем удобнее всего это сделать, предполагая зависимость линейной.

Наконец, во всех сложных случаях, когда регрессия заведомо будет нелинейной, изучение линейной регрессии можно использовать как первый этап исследования, с тем, чтобы в дальнейшем внести в нее необходимые поправки.

Пользуясь принципом наименьших квадратов, легко составить нормальные уравнения линейной регрессии:

.

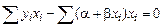После простых преобразований приводим систему к виду (m – объем выборки)

.

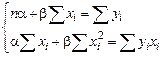Число b называется коэффициентом регрессии; его легко найти с помощью определителей:

.

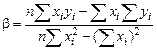Число a называется свободным членом регрессии. Его тоже нетрудно найти с помощью определителей, но проще выразить его из первого уравнения через найденное уже b

.

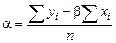Полученные формулы полностью определяют линейную регрессию по заданной выборке. Это равенство можно переписать в виде:

,

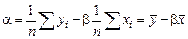откуда

.

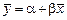Таким образом, средняя точка 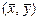совместного распределения изучаемых величин всегда лежит на линии регрессии. Отсюда вытекает, что для определения линии регрессии достаточно знать лишь ее угловой коэффициент b.

Перейдем к оценке силы найденной связи. Тот факт, что исследуемая зависимость предполагается линейной, позволяет использовать для оценки силы связи выборочный коэффициент корреляции r. Можно показать, что r и b связаны между собой

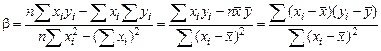
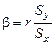, откуда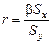

или в развернутом виде

.

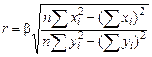Если коэффициент корреляции был вычислен ранее, то можно использовать обратную замену b на r.

Мы получим уравнение регрессии в виде

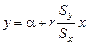
или, заменяя a на 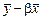, в виде

.

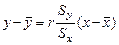Связь между случайными величинами. Корреляция

До сих пор изучали наблюдения над одной случайной величиной. Между тем для выяснения тех или иных причинно–следственных связей в окружающей природе необходимо вести одновременные наблюдения над целым рядом случайных величин, чтобы по полученным данным изучать взаимоотношения этих величин. Ограничимся пока двумя случайными величинами Х и У.

В математическом анализе зависимость между двумя величинами выражается понятием функции у = f (x), где каждому допустимому значению одной переменной соответствует одно и только одно значение другой переменной. Такая зависимость называется функциональной, она обнаруживается с помощью строгих логических доказательств и не нуждается в опытной проверке. Если у = const при изменении х, то говорят, что у не зависит от х.

Гораздо сложнее обстоит дело с понятием зависимости случайных величин: если при изменении х изменилось у, мы не можем сказать, является ли это изменение результатом зависимости у от х или это результат влияния случайных факторов. Здесь имеет место связь особого рода, при которой с изменением одной величины меняется распределение другой – такая связь называется стохастической.

Выявление стохастической связи и оценка ее силы представляют задачу математической статистики.

Рассматривая свойства дисперсии, мы указали, что дисперсия суммы двух независимых величин равна сумме дисперсий этих величин. Поэтому если для двух случайных величин Х и У окажется, что

,

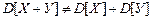то это служит верным признаком наличия зависимости между Х и У, т.е. корреляции.

Из этого неравенства вытекает (доказано), что справедливо следующее неравенство:

,

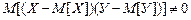где 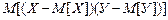называют корреляционным моментом.

Корреляционный момент зависит от единиц измерения величин Х и У. Поэтому на практике чаще используется безразмерная величина, которая называется коэффициентом корреляции.

.