
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример 4.2.
|
|
Методом северо-западного угла составить опорный план следующей задачи:
| Вj Аi | 
| 
| 
| Предложение | ||||||||||

| ||||||||||||||

| ||||||||||||||
| Спрос | ||||||||||||||
В правом верхнем углу каждой клетки таблицы указывается стоимость перевозки единицы груза.
Начнем заполнение таблицы перевозок с верхнего («северо-западного») угла. Потребителю  требуется 80 единиц груза. Эти 80 единиц груза могут быть доставлены от первого поставщика
требуется 80 единиц груза. Эти 80 единиц груза могут быть доставлены от первого поставщика  . Поэтому запишем в клетку
. Поэтому запишем в клетку  количество перевозок
количество перевозок  и поставим прочерк в клетку (2, 1).
и поставим прочерк в клетку (2, 1).
Поставщик  требует, чтобы с его предприятия было вывезено 100 единиц груза, а пока вывезено только 80. Увезем оставшийся груз к потребителю
требует, чтобы с его предприятия было вывезено 100 единиц груза, а пока вывезено только 80. Увезем оставшийся груз к потребителю  . Запишем
. Запишем  остающиеся у поставщика
остающиеся у поставщика  20 единиц груза и поставим прочерк в (1, 3).
20 единиц груза и поставим прочерк в (1, 3).
| Вj Аi | 
| 
| 
| Предложение | ||||||||||

| ||||||||||||||
| - | ||||||||||||||

| ||||||||||||||
| - | ||||||||||||||
| Спрос | ||||||||||||||
Займемся теперь потребителем  . Ему требуется 90 единиц груза, а пока доставлено от
. Ему требуется 90 единиц груза, а пока доставлено от  только 20. Недостающие 70 единиц доставим от поставщика
только 20. Недостающие 70 единиц доставим от поставщика  . Продолжая заполнять таблицу, позаботимся об удовлетворении поставщика
. Продолжая заполнять таблицу, позаботимся об удовлетворении поставщика  . От него вывезено 70 единиц груза, в то время как требуется вывезти 200. Увезем оставшийся груз к потребителю
. От него вывезено 70 единиц груза, в то время как требуется вывезти 200. Увезем оставшийся груз к потребителю  и, поскольку наша транспортная задача сбалансирована, именно эти оставшиеся у поставщика
и, поскольку наша транспортная задача сбалансирована, именно эти оставшиеся у поставщика  130 единиц груза и нужны потребителю
130 единиц груза и нужны потребителю  .
.
В результате такой методики заполнения таблицы перевозок мы удовлетворили требования всех поставщиков и потребителей (т.е. все ограничения задачи). При этом видно, что из шести клеток таблицы перевозок мы заполнили четыре. Две клетки остались пустыми. Таким образом, мы получили опорный план.
Метод минимального элемента позволяет построить начальный опорный план транспортной задачи и является вариантом метода северо-западного угла, учитывающим специфику матрицы С = (сij)m∙ n В отличие от метода северо-западного угла данный метод иногда позволяет сразу получить достаточно экономичный план и сокращает общее количество итераций по его оптимизации.
Схема метода.

1 шаг. Выбираем клетку матрицы соответствующую min cij, т.е
Полагаем хij = min(ai, bj).
Возможны три случая:

а) если ai < bj, то хij = аi и оставшуюся часть i -й строки, заполняют прочерками, полагают bj: = bj - аi
б) если ai > bj, то хij = bj, и оставшиеся элементы j -го столбца заполняют прочерками, полагают ai: = ai - bj
в) если ai = bj, то хij = аi = bj, а все оставшиеся элементы j -го столбца или i -й строки заполняют прочерками, полагают либо ai = 0, если столбец заполнен прочерками, либо bj = 0, если строка заполнена прочерками.
Затем проделывают первый и второй шаг с оставшейся незаполненной частью матрицы Х.
ПРИМЕР 4.3. Методом минимального элемента составить опорный план ТЗ из примера 4.2.
Итак, исходные данные:
Матрица стоимостей С = 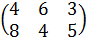 ,
,
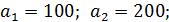
b1 =80; b2 =90; b3 =130.
min cij =c13=3, помещаем перевозку x13 = min(100, 130) = 100 в соотвутствующую клетку. Поскольку от первого поставщика всё вывезено, ставим прочерки в клетки (1, 1), (1.2). Третьему потребителю осталось поставить 30 единиц.
| - | - | |
Для незаполненной части соответствующий минимальный элемент матрицы стоимости c22 = 4. Помещаем в матрицу перевозок
x22 = min (90, 200) = 90. У второго поставщика осталось 110 единиц, из которых 30 будет поставлено третьему потребителю и 80 – четвёртому.
| - | - | |
X(0) =
4.5. Метод потенциалов решения транспортной задачи
Для транспортной задачи (ТЗ), как и для любой ЗЛП, существует двойственная к ней задача.
Исходная задача:
 (4.7)
(4.7)
 (4.8)
(4.8)
 (4.9)
(4.9)
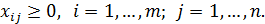 (4.10)
(4.10)
Обозначим двойственные переменные для каждого ограничения вида (4.8) через Ui (i = 1,..., m) и вида (4.9) – Vj (j = 1,..., n), тогда двойственная задача имеет вид
 (4.11)
(4.11)
 (4.12)
(4.12)
Переменные задачи, двойственной к транспортнoй, Ui и Vj, называют потенциалами.
Теорема 4.3. Для оптимальности плана X = (xij)m∙ n ТЗ необходимо и достаточно существования чисел (потенциалов) V1, V2,..., Vn и U1, U2,..., Um, таких, что:


Доказательство:
1. Необходимость
Дано:
ТЗ - разрешима, следовательно, по 3-й теореме двойственности
двойственная к ТЗ тоже разрешима, т.е. выполняются ограничения
 , что доказывает необходимость условия 1.
, что доказывает необходимость условия 1.
Далее по 4-й теореме двойственности выписываются условия нежесткости, которые для данной пары ТЗ и ДТЗ примут вид:

Откуда очевидно, что если
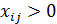 , то
, то  или
или  ,
,
что доказывает необходимость условия 2.
2. Достаточность.
Даны числа  , удовлетворяющие условиям 1 и 2.
, удовлетворяющие условиям 1 и 2.
Из 1 следует, что  образуют план ДТЗ.
образуют план ДТЗ.
Покажем, что для планов ТЗ и ДТЗ выполняется условие 4-й теоремы двойственности (теоремы нежесткости). Действительно, если  , то
, то
 .
.
Если  > 0, то на основании условия 2
> 0, то на основании условия 2  ,
,
т.е. выполняется условие
 .
.
Т.е. планы  и
и  являются оптимальными планами своих задач на основании 4-й теоремы двойственности.
являются оптимальными планами своих задач на основании 4-й теоремы двойственности.
Из теоремы следует: для того чтобы опорный план был оптимальным, необходимо выполнение следующих условий:
а) для каждой занятой клетки (отличного от нуля элемента матрицы Х) сумма потенциалов должна быть равна стоимости перевозки единицы груза
 ; (4.13)
; (4.13)
б) для каждой незанятой клетки (xij = 0) сумма потенциалов должна быть меньше или равна стоимости перевозки единицы груза
 . (4.14)
. (4.14)
Таким образом, для проверки плана на оптимальность необходимо сначала построить систему потенциалов. Для построения системы потенциалов используем условие  , xij > 0.
, xij > 0.
Систему потенциалов можно построить только для невырожденного опорного плана. Такой план содержит m + n – 1 занятых клеток, поэтому для него можно составить систему из m + n – 1 линейно-независимых уравнений вида (4.13) с неизвестными Ui и Vj. Уравнений на одно меньше, чем переменных, поэтому система является неопределенной и одному неизвестному (обычно Ui) придают нулевое значение. После этого остальные потенциалы определяются однозначно.
Проверка выполнения условия оптимальности для незанятых клеток
Просматриваем строки и для каждой незанятой клетки проверяем выполнения условия (4.14), т.е. суммируем потенциалы тех строк и столбцов, на пересечении которых стоит незанятая клетка. Если для всех незанятых клеток Ui + Vj ≤ cij, то по теореме (4.3) проверяемый план является оптимальным. Если для некоторых клеток Ui + Vj > cij, то план является неоптимальным. Тогда для каждой клетки, в которой не выполняется условие оптимальности, находим величину (Ui + Vj) – cij > 0.
Выбор клетки, в которую необходимо поместить перевозку
Загрузке подлежит в первую очередь клетка, которой соответствует
max ((Ui + Vj) – cij).
Построение цикла и определение величины перераспределения груза
Для определения количества единиц груза, подлежащих перераспределению, отмечаем знаком «+» незанятую клетку, которую надо загрузить. Это означает, что клетка присоединяется к занятым клеткам. Занятых клеток стало m + n, поэтому появляется цикл, все вершины которого за исключением клетки, отмеченной знаком «+», находятся в занятых клетках, причем этот цикл единственный. Отыскиваем цикл и, начиная движение от клетки, отмеченной знаком «+», поочередно проставляем знаки «–» и «+». Затем находим  = min xij, где xij – перевозки, стоящие в вершинах цикла, отмеченных знаком «–». Величина
= min xij, где xij – перевозки, стоящие в вершинах цикла, отмеченных знаком «–». Величина  определяет, сколько единиц груза можно перераспределить по найденному циклу. Значение
определяет, сколько единиц груза можно перераспределить по найденному циклу. Значение  записываем в незанятую клетку, отмеченную знаком «+». Двигаясь по циклу, вычитаем
записываем в незанятую клетку, отмеченную знаком «+». Двигаясь по циклу, вычитаем  из объемов перевозок, расположенных в клетках, которые отмечены знаком «–», и прибавляем к объемам перевозок, находящихся в клетках, отмеченных знаком «+». Если
из объемов перевозок, расположенных в клетках, которые отмечены знаком «–», и прибавляем к объемам перевозок, находящихся в клетках, отмеченных знаком «+». Если  соответствует несколько минимальных перевозок, то при вычитании оставляем в соответствующих клетках нулевые перевозки в таком количестве, чтобы во вновь полученном опорном плане занятых клеток было
соответствует несколько минимальных перевозок, то при вычитании оставляем в соответствующих клетках нулевые перевозки в таком количестве, чтобы во вновь полученном опорном плане занятых клеток было
m + n – 1.
Проверка нового плана на оптимальность
Для проверки на оптимальность опорного плана нужно вновь построить систему потенциалов и проверить выполнение условия оптимальности для каждой незанятой клетки. Если полученный план снова окажется неоптимальным, то следует выполнить вычисления, приведенные в предыдущем пункте. Процесс повторяют до тех пор, пока все незанятые клетки не будут удовлетворять условию (4.13).
Пример 4.4. Решить ТЗ:
| Vj Ui | 
| 
| 
| 
| Предложение | |||||||||||

| ||||||||||||||||

| ||||||||||||||||

| ||||||||||||||||
| Спрос | ||||||||||||||||
Условие баланса выполнено. Следовательно, имеем ТЗ закрытого типа.
Предварительный этап: находим исходный опорный план X° методом «минимального элемента».
Таблица 4.3.
| Vj Ui | 
| 
| 
| 
| ||||||||

| ||||||||||||
| - | - | |||||||||||

| ||||||||||||
| - | - | |||||||||||

| ||||||||||||
| - | - |
Число занятых клеток равно 6 и совпадает с рангом матрицы ограничений ТЗ:
r = m + n – 1 = 3 + 4 – 1 = 6.
Итерация 1. Для проверки полученного опорного плана на оптимальность находим систему потенциалов для занятых клеток (xij > 0).
Для этого, например, полагаем U1 = 0 (записываем U1 = 0 слева в табл. 4.4).
Таблица 4.4.
| Vj Ui | 
| 
| 
| 
| |||||||||

| |||||||||||||
| - | 100+ | 100- | - | ||||||||||

| -2 | ||||||||||||
| 150- | - | 150+ | - | ||||||||||

| |||||||||||||

| 50- | - | |||||||||||
Далее, исходя из занятых клеток (1, 2) и (1, 3), находим V2 = 4 – 0 = 4, V3 = 6 – 0 = 6 (записываем сверху в таблице). На основе базисной клетки (2, 3) получаем U2 = 2 – 6 = –4, затем V1 = 1 – (–4) = 5; U3 = 3 – 4 = –1; V4 = 2.
Далее вычисляем сумму потенциалов для каждой из свободных клеток и записываем их в верхнем левом углу. Так как для клеток (3, 1) и (3, 3) критерий оптимальности не выполняется:
U3 + V1 = 4 > 2,
U3 + V3 = 5 > 3,
то полученный опорный план не оптимальный. Так как
D31 = U3 + V1 – cij = 2 = D33,
то в любую из клеток, например, в (3, 1), проставляем некоторое число  .
.
Для того чтобы не нарушился баланс в 3-й строке, вычитаем  из величины перевозки, стоящей в клетке (3, 2), прибавляем к x12 = 100, вычитаем от x13, прибавляем к x23 и вычитаем от x21, т.е. составляем цикл:
из величины перевозки, стоящей в клетке (3, 2), прибавляем к x12 = 100, вычитаем от x13, прибавляем к x23 и вычитаем от x21, т.е. составляем цикл:
(3, 1) → (3, 2) → (1, 2) → (1, 3) → (2, 3) → (2, 1) → (3, 1).
Знаки «+» и «–» в клетках чередуются.
Заметим, что движение от одной клетки к другой происходит только по занятым, кроме первой, в которую проставляется  . Максимальное значение
. Максимальное значение  равно наименьшему уменьшаемому:
равно наименьшему уменьшаемому:  = 50. Если
= 50. Если  взять больше, то получаем отрицательную величину в плане перевозок, а если меньше, то нарушается опорность плана.
взять больше, то получаем отрицательную величину в плане перевозок, а если меньше, то нарушается опорность плана.
Новый опорный план приведен в табл. 4.5
Таблица 4.5.
| Vj Ui | 
| 
| 
| 
| |||||||||

| |||||||||||||
| - | 50- | 
| |||||||||||

| |||||||||||||
| 100- | - | 200+ | - | ||||||||||

| |||||||||||||
| 50+ | - | 50- | |||||||||||
Итерация 2. Проверяем полученный план X(1) на оптимальность. Находим систему потенциалов (они записаны в таблице слева и сверху). Вычисляем сумму потенциалов для свободных клеток (записаны в левом верхнем углу клетки). Так как
U1 + V4 = 4 > 3,
то план X(1) не является оптимальным. Для построения нового опорного плана проставляем величину  в клетку (1, 4) и составляем цикл:
в клетку (1, 4) и составляем цикл:
(1, 4) → (3, 4) → (3, 1) → (2, 1) → (2, 3) → (1, 3) → (1, 4).
Определяем значение  = 50, при этом две клетки (1, 3) и (3, 4) обращаются в нулевые. Следовательно, план Х(2) будет вырожденным. Для дальнейшего решения необходимо оставить нуль в одной из клеток и считать ее за базисную. Целесообразнее нуль оставить в клетке с меньшей стоимостью перевозок, т.е. в клетке (3, 4). Новый опорный план приведен в табл. 4.6.
= 50, при этом две клетки (1, 3) и (3, 4) обращаются в нулевые. Следовательно, план Х(2) будет вырожденным. Для дальнейшего решения необходимо оставить нуль в одной из клеток и считать ее за базисную. Целесообразнее нуль оставить в клетке с меньшей стоимостью перевозок, т.е. в клетке (3, 4). Новый опорный план приведен в табл. 4.6.
Таблица 4.6.
| Vj Ui | 
| 
| 
| 
| |||||||||

| |||||||||||||
| - | - | ||||||||||||

| |||||||||||||
| - | - | ||||||||||||

| |||||||||||||
| - | - | ||||||||||||
Итерация 3. Число занятых клеток равно 6. Находим значения потенциалов и их сумму для свободных клеток. Критерий оптимальности выполняется:
Ui +Vj ≤ cij для xij = 0; i = 1, m; j = 1, n,
поэтому полученный план является оптимальным:
 и f (X*) = 1500.
и f (X*) = 1500.
Пример 4.5. Решить задачу:
| Vj Ui | V1 | V2 | V3 | Предложение | ||||||||
| U1 | ||||||||||||
| U2 | ||||||||||||
| U3 | ||||||||||||
| Спрос |
Решение. Объем ресурсов: 80 + 60 + 60 = 200 – превышает общие потребности 30 + 70 + 60 = 160 на 40 ед., следовательно, ТЗ является задачей открытого типа. Вводим дополнительный (балансовый) пункт потребления с объемом потребностей b4 = 40 и полагаем
c14 = c24 = c34 = 0. В результате получаем ТЗ закрытого типа.
Предварительный этап. Находим исходный опорный план  методом «минимального элемента» (табл. 4.7).
методом «минимального элемента» (табл. 4.7).
Таблица 4.7.
| Vj Ui | ||||||||||||
| 10– | ||||||||||||

| ||||||||||||
| –2 | ||||||||||||
| 20+ | 40– | |||||||||||
| –2 | ||||||||||||
Данный план является вырожденным, поэтому ставим «0» – перевозку в клетку с минимальным значением cij, но так, чтобы не образовалось замкнутого маршрута (цикла). В нашем примере c14 = c34 = 0, но занять клетку (1, 4) нельзя, так как образуется цикл:
(1, 4) → (2, 4) → (2, 1) → (1, 1) → (1, 4).
Поэтому ставим «0» в клетку (3, 4).
Итерация 1. Проверяем план  на оптимальность. Положив
на оптимальность. Положив  , находим потенциалы (см. табл. 4.7). Далее находим сумму потенциалов для свободных клеток (они записаны в левом верхнем углу клетки). Так как
, находим потенциалы (см. табл. 4.7). Далее находим сумму потенциалов для свободных клеток (они записаны в левом верхнем углу клетки). Так как
 ;
;
 ,
,
то полученный опорный план  неоптимальный. Для клеток (1, 4) и (3, 1) оценки одинаковы:
неоптимальный. Для клеток (1, 4) и (3, 1) оценки одинаковы:  и
и  , поэтому выбираем любую, например, (1, 4). Проставляем в эту клетку
, поэтому выбираем любую, например, (1, 4). Проставляем в эту клетку  и составляем цикл, чередуя знаки «+» и «–»; получим
и составляем цикл, чередуя знаки «+» и «–»; получим  . Новый опорный план
. Новый опорный план  представлен в табл. 4.8.
представлен в табл. 4.8.
Таблица 4.8.
| Vj Ui | ||||||||||||
| 30– | 30+ | |||||||||||

| 0– |
Итерация 2. Находим систему потенциалов (см. слева и сверху табл. 4.8). Сумма потенциалов для небазисных клеток записана в левом верхнем углу. Критерий оптимальности не выполняется для клетки (3, 1):  .
.
Проставим в эту клетку  и составим замкнутую цепочку, в результате получаем
и составим замкнутую цепочку, в результате получаем  . Опорный план
. Опорный план  представлен в таблице 4.9.
представлен в таблице 4.9.
Итерация 3. Найдя систему потенциалов, убеждаемся в оптимальности плана  (табл. 4.9).
(табл. 4.9).
Таблица 4.9.
| Vj Ui | ||||||||||||
| –2 | -2 | |||||||||||
Транспортные издержки составляют 480 и  . Так как четвертый потребитель фиктивный, то 10 ед. груза останутся у первого поставщика, 30 ед. – у второго.
. Так как четвертый потребитель фиктивный, то 10 ед. груза останутся у первого поставщика, 30 ед. – у второго.
Пример 4.6.Методом потенциалов решите следующую ТЗ:
| Vj Ui | 
| 
| 
| 
| Предложение | ||||||||||||

| |||||||||||||||||

| - | ||||||||||||||||

| - | ||||||||||||||||
| Спрос | |||||||||||||||||
Прочерк между пунктами A2 и B2, A3 и B4 означает, что перевозки между указанными пунктами запрещены.
Проверяем условие баланса:
80 + 320 + 150 = 550 = 250 + 100 + 150 + 50.
Для решения задачи полагаем, что стоимости перевозки единицы груза по запрещенным маршрутам равны достаточно большому числу М > 0. Далее эта М-задача решается обычным методом потенциалов, но потенциалы будут зависеть от коэффициента М. Если оптимальный план М-задачи содержит положительные перевозки по запрещенным маршрутам, то исходная ТЗ неразрешима (множество ее планов пусто). В противном случае получаем решение исходной ТЗ.
Предварительный этап. Составляем методом «минимального элемента» исходный опорный план  (табл. 4.10).
(табл. 4.10).
Итерация 1. Вычисляем потенциалы и проверяем план на оптимальность (см. табл. 4.10).
Таблица 4.10.
| Vj Ui | 10 – M | 7 – M | ||||||||||||
| 10-M | 7-M | |||||||||||||
| M – 2 | M | M-1 | ||||||||||||
| 20– | 
| |||||||||||||
| 12-M | 9-M | M | ||||||||||||
| 80+ | 70– | |||||||||||||
В клетке (2, 3) имеем
 ,
,
т.е. план  не является оптимальным. Проставляем в эту клетку
не является оптимальным. Проставляем в эту клетку  и составляем замкнутый маршрут. Получаем
и составляем замкнутый маршрут. Получаем  . Опорный план
. Опорный план  приведен в табл. 4.11.
приведен в табл. 4.11.
Итерация 2. Проверяем план  на оптимальность. Так как для всех свободных клеток
на оптимальность. Так как для всех свободных клеток
 ,
,
то план  – оптимальный и не содержит положительных перевозок по запрещенным маршрутам.
– оптимальный и не содержит положительных перевозок по запрещенным маршрутам.
Таблица 4.11.
| Vj Ui | v1 = 3 | v2 = 2 | v3 = 1 | v4 = 0 | ||||||||
| u1 = 0 | ||||||||||||
| u2 = 5 | M | |||||||||||
| u3 = 2 | M | |||||||||||
Минимальные транспортные расходы составляют 3000.
Определение оптимального плана транспортных задач,
имеющих некоторые усложнения в их постановке
1. При некоторых реальных условиях перевозки груза из определенного пункта Ai в пункт назначения Bj не могут быть осуществлены. Для определения оптимальных планов таких задач предполагают, что стоимость перевозки единицы груза из пункта Ai в пункт Bj является сколь угодно большой величиной М и при этом условии известными методами находят решение ТЗ. Такой подход к нахождению решения ТЗ называется запрещением перевозок.
2. В отдельных ТЗ дополнительным условием является обеспечение перевозки по соответствующим маршрутам определенного количества груза. Пусть, например, из Ai в Bj требуется обязательно перевезти α ij единиц груза. Тогда в соответствующую клетку таблицы, находящуюся на пересечении строки Ai и столбца Bj, записывают указанное число α ij и в дальнейшем считают эту клетку свободной со сколь угодно большой стоимостью перевозки М. Для полученной таким образом новой ТЗ находят оптимальный план, который определяет оптимальный план исходной задачи.
3. Иногда требуется найти решение ТЗ, при котором из Ai в Bj должно быть перевезено не менее заданного количества груза α ij. Для определения оптимального плана такой задачи считают, что запасы Ai и потребности Bj меньше фактических на α ij единиц. После этого находят оптимальный план новой ТЗ, на основании которого и определяют решение исходной задачи.
Примечание: При целых ai (i = 1,..., m) и bj (j = 1,..., n), в силу специфики ограничений ТЗ, любое базисное допустимое решение является целочисленным.
|
|