Метод равных треугольиков

Суть метода заключается в том, что, исходя из условия задачи, отыскивают равные треугольники и применяют их свойства. При этом равные треугольники можно непосредственно найти по данным или при помощи дополнительных построений.

КЛЮЧЕВЫЕ ЗАДАЧИ

1. Доказать, что в равнобедренном треугольнике медианы, проведенные к боковым сторонам равны.

2. Через произвольную точку внутри квадрата проведены две взаимно перпендикулярные прямые, каждая из которых пересекает две противоположные стороны квадрата. Докажите, что отрезки этих прямых, заключённые внутри квадрата, равны.

3. Диагонали трапеции равны. Докажите, что трапеция равнобедренная.

ЭЛЕМЕНТАРНЫЕ ЗАДАЧИ

4. Дан треугольник ABC (AC< BC). Внешне построены квадраты BMNC и CPQA. Докажите, что AN = BP.

5. На стороне AB треугольника ABC взята точка D, а на стороне A₁B₁ треугольника A₁B₁C₁ взята точка D₁. Известно, что треугольники ADC и A₁D₁C₁ равны и отрезки BD и B₁D₁ также равны. Докажите равенство треугольников ABC и A₁B₁C₁.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

6. Докажите, что в треугольнике перпендикуляры, проведённые из концов любой стороны к медиане этой стороны, равны.

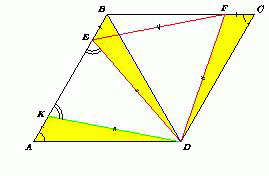
7. Точки E и F лежат на сторонах соответственно AB и BC ромба ABCD, причём AE= 5 BE, BF= 5 CF. Известно, что DEF – равносторонний. Найдите угол BAD.

8. Докажите, что если диагонали четырёхугольника делят друг друга пополам, то противоположные стороны четырёхугольника - равны.

9. В остроугольном треугольнике ABC высоты AA ₁и CC ₁пересекаются в точке H. Известно, что H – середина AA ₁, а CH: HC ₁ = 2: 1. Найдите величину угла B.

10. Доказать, что биссектриса угла есть геометрическое место точек, равноудаленных от его сторон.

11.

№1 Доказать, что в равнобедренном треугольнике медианы, проведенные к боковым сторонам равны.

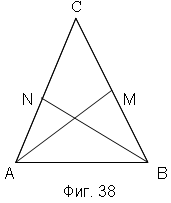
Дано:

∆ АВС – равнобедренный

АМ, BN – медианы

Доказать: АМ = BN

Доказательство:

Пусть ∆ ABC – равнобедренный, с основанием AB, AM и BN являются биссектрисой CAB и CBA (рис.1) Треугольники AMB и BNA равны (по второму признаку):
1. CAB = CBA.
2. сторона AB – общая.
3. MAB = NBA = ¹/₂ CAB. Отрезки AM и BN являются соответствующими в этих равных треугольниках, и, следовательно, AM = BN.

ч.т.д.

[https://www.matematike.net/geometria/zadachi-na-priznak-ravnosri-treugolnikov-storona-storona-storona.html]

№2 Через произвольную точку внутри квадрата АВСD проведены две взаимно перпендикулярные прямые L, L₁, каждая из которых пересекает две противоположные стороны квадрата. Докажите, что отрезки этих прямых, заключённые внутри квадрата, равны.

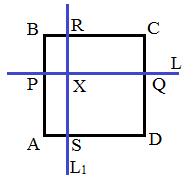
Дано:

АВСD – квадрат

L, L₁ – прямые

L _┴ L₁

BC∩ L₁= R, AD∩ L₁= S

AB∩ L= P, CD∩ L= Q

Доказать: RS=PQ

Доказательство:

Через точку Х, расположенную внутри квадрата АВСD, проведём две взаимно перпендикулярные прямые L, L₁.

Пусть BC∩ L₁= R, AD∩ L₁= S, AB∩ L= P, CD∩ L= Q.

Докажем что RS=PQ.

Пусть Е – проекция точки Q на AB, а F – проекция точки R на AD. Прямоугольные треугольники PEQ ‍ и SFR‍ равны по катету и прилежащему острому углу. Поэтому PQ = RS.

[Элементарная геометрия. Планиметрия.Жак Саломон Адамар М., ОГИЗ, 1948. 608 с.]

№3 Диагонали трапеции равны. Докажите, что трапеция равнобедренная.

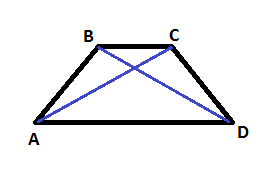
Дано:

АВСD – трапеция

AC, BD– диагонали

AC=BD

Доказать: АВСD – равнобедренная

Доказательство:

Через вершину C меньшего основания BC трапеции ABCD проведём прямую, параллельную диагонали BD. Пусть эта прямая пересекает продолжение основания AD в точке K. Поскольку BCKD параллелограмм, CK = BD = AC, поэтому треугольник CKA равнобедренный. Значит, ∠ BDA = ∠ CKA = ∠ CAD. Треугольники ABD и DCA равны по двум сторонам и углу между ними, поэтому ∠ BAD = ∠ CDA. Следовательно, трапеция ABCDравнобедренная.

[Борис Николаевич Делоне, О. К. Житомирский М.-Л., ОГИЗ, 1949. 304 с.]

№4 Дан треугольник ABC (AC< BC). Внешне построены квадраты BMNC и CPQA. Докажите, что AN = BP.

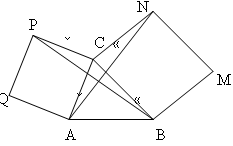
Дано:

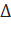АВС (AC < BC),

BMNC и CPQA – квадраты.

Доказать: AN = BP.

Доказательство:

Для треугольников BPC и ACN BC = CN (BMNC – квадрат);
PC = AC (CPQA – квадрат) угол BCP = ACN = 90° + ACB. Поэтому, треугольники равны и откуда AN = BP.

ч.т.д.

[https://www.matematike.net/geometria/zadachi-na-priznak-ravnosri-treugolnikov-storona-storona-storona.html]

№5 На стороне AB треугольника ABC взята точка D, а на стороне A₁B₁ треугольника A₁B₁C₁ взята точка D₁. Известно, что треугольники ADC и A₁D₁C₁ равны и отрезки BD и B₁D₁ также равны. Докажите равенство треугольников ABC и A₁B₁C₁.

В В₁ Дано:

АВС, А₁В₁С_1,

D 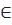ВС, D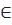₁ В₁С_1,

D D₁ АDС, А₁D₁С_1,

BD=D₁B₁

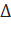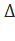Доказать: АВС = А₁В₁С₁А С А₁ С₁

Доказательство:

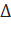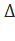Рассмотрим АВС, А₁В₁С₁:

1) АС=А₁С₁;

2) 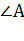= 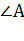₁;

3) Т.к. A₁D₁=AD, DB=D₁B₁, то АВ=А₁В₁=> ∆ АВС= 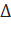А₁В₁С₁(по I признаку)

ч.т.д.

[https://www.zadachi.mccme.ru]

№6 Докажите, что в треугольнике перпендикуляры, проведённые из концов любой стороны к медиане этой стороны, равны.

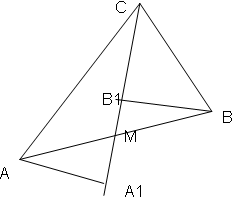
Дано:

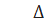АВС, СМ – медиана,

AA₁ и BB₁ –перпендикуляры.

Доказать: AA₁ = BB₁.

Доказательство:

Треугольники AA₁M и BB₁M – равны (по признаку " угол-сторона-угол") потому что BB₁M = AA₁M = 90°, AMA₁ = BMB₁ как вертикальные, AM=BM. Тогда AA₁ = BB₁ как соответствующие стороны в этих треугольниках.

ч.т.д.

[https://www.matematike.net/geometria/zadachi-na-priznak-ravnosri-treugolnikov-storona-storona-storona.html]

№7 Точки E и F лежат на сторонах соответственно AB и BC ромба ABCD, причём AE = 5 BE, BF= 5 CF. Известно, что треугольник DEF – равносторонний. Найдите угол BAD.

Дано:

АВСD – ромб

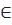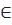E AB, F BC

AE = 5BE

BF=5CF

∆ DEF – равносторонний

Найти: 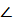BAD.