Построение компьютерной модели трубчатого реактора в нестационарном режиме.

2.1. Основные допущения:

· изотермический режим;

· однопараметрическая диффузионная модель.

2.2. Уравнение математического описания:

Уравнение 1) является дифференциальным уравнением в частных производных второго порядка параболического типа с двумя независимыми переменными t и 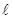и описывает нестационарный режим трубчатого реактора, в котором протекает единственная простейшая реакция, если принята однопараметрическая диффузионная модель для потока.

Необходимо найти:

Начальное условие:

Граничные условия:

Для решения системы дифференциальных уравнений в частных производных (СДУЧП) может быть использован метод дискретизации, в соответствии с которым производные представляются в конечно-разностной форме в определённом интервале и/или [0, L ] в результате чего уравнение 1) с начальным 1’) и граничными 1’’) условиями превращаются в систему обыкновенных дифференциальных уравнений (СОДУ) и/или в систему конечных уравнений (СКУ).

Для этого уравнения можно использовать три варианта дискретизации:

1) По независимой переменной :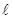

В результате получается система обыкновенных дифференциальных уравнений 1-го порядка с независимой переменной t.

2) По независимой переменной t:

В результате получается система обыкновенных дифференциальных уравнений 2-го порядка с независимой переменной .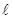

3) По независимым переменным 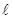и t:

В результате получается система конечных уравнений.

Детально рассмотрим 1-й вариант дискретизации по независимой переменной :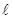

При 0 < 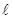< L конечно-разностное представление производных имеет вид:

- Производная «по недостатку»:

- Производная «по избытку»:

- Вторая производная:

В этом случае граничные условия 1’’) равны:

В результате из одного уравнения в частных производных вследствие дискретизации получается система (n -1) обыкновенных дифференциальных уравнений с независимой переменной t и начальным условием 1’), представленным в дискретном виде:

Если для конечно-разностного представления производной использовать «производную по избытку», то система обыкновенных дифференциальных уравнений с начальными условиями имеет вид:

Преобразуя уравнение и

предполагая, что его параметры являются константами (D, W и k), можно получить следующую систему обыкновенных дифференциальных уравнений:

или

где

Из изложенного следует, что система уравнений включает граничные условия и в матричном виде может быть представлена:

где 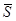- вектор с граничными условиями, а начальные условия являются дискретным представлением начального условия

Полученная система неоднородных обыкновенных дифференциальных уравнений может быть легко решена любым из известных методов (например, методом Эйлера или Рунге-Кутта), тем более потому, что матрица её коэффициентов является трёхдиагональной.

Тема 6
Введение

Обозначения:

Нумерация тарелок сверху вниз

Тарелка 1 – конденсатор или дефлегматор

Тарелка N – кипятильник куба

1. Основные допущения:

в колонне только две фазы – жидкость и пар;

дополнительных отборов потоков с промежуточных тарелок, кроме куба и конденсатора, не происходит;

в межтарельчатом пространстве нет контакта между фазами;

межтарельчатый унос жидкости отсутствует;

на тарелках колонны протекает только процесс массопередачи.

2. Особенности модели:

рассматривается n -компонентная смесь, например, концентрация жидкости на тарелке i может быть представлена:

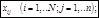
на каждую тарелку может подаваться поток жидкого питания Fi с концентрацией:

на каждую тарелку может подводиться или отводиться поток тепла Δ Q ^П

(Δ Q ^П - положительный: тепло подводится, Δ Q ^П - отрицательный: тепло отводится);

эффективность массопередачи на тарелке оценивается с использованием модифицированного КПД Мерфри для многокомпонентных смесей:

где 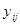- состав паровой фазы в долях, покидающей тарелку i

- состав паровой фазы в долях, поступающей на тарелку i с тарелки i+ 1;

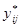- равновесный состав паровой фазы в долях на тарелке i;

равновесный состав паровой фазы на тарелке i определяется по формуле:

где K_ij - константа фазового равновесия на i – ой тарелке для j – го компонента;

x_ij - состав жидкой фазы в долях на тарелке i.

Таким образом, для построения модели необходимо:

построить модель фазового равновесия жидкость-пар;

построить модель процесса разделения на тарелке с учётом её эффективности (2), т.е. с учётом многокомпонентной массопередачи;

построить модель тарельчатой ректификационной колонны, т.е. каскада тарелок с потоками питания F_i и потоками подводимого (отводимого) тепла ;