Разделы сайта

Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

I. МЕХАНИКА. I.1. Пусть расстояние между столбами равно S , скорость велосипе-диста в момент проезда первого столба равна v0

⇐ ПредыдущаяСтр 21 из 27Следующая ⇒

I.1. Пусть расстояние между столбами равно S, скорость велосипе-диста в момент проезда первого столба равна v 0, а его ускорение равно a. Кинематические уравнения движения велосипедиста на заданных в

условии отрезках пути имеют вид:

S = v 0 t + at 2, S = (v 0+ at) t 2+ at 2, S = (v 0+ at + at 2) t 3+ at 2.

Вводя обозначения t 0= 2 v 0, t= 2 S, последнее из этих уравнений

приведем к виду:

t 3+ 2(t + t 2+(t 0/2)) t 3− t2= 0.

Условию задачи удовлетворяет положительный корень этого уравнения:

t 3= − (t + t 2+(t 0/2))+ (t + t 2+(t 0/2))2+t2.

Чтобы получить ответ, осталось найти t 0и t. Для этого воспользуемся первым и вторым кинематическими уравнениями движения велосипе-диста, которые в наших обозначениях принимают вид:

1 1

2 2

t = t 0 t + t 2, t = (t 0+2 t) t 2+ t 2. Решая эту систему, находим

t 0= t 2− 1+212=1 с, 1 2

1 1

t=(t + t 2) t t 2=6с2.

1 2

Следовательно, t 3= − 3, 5+ 3, 52+6» 0, 77 с.

Физический факультет

I.2. Пусть v 0– скорость автопоезда при равномерном движении, F – сила тяги двигателя тягача, постоянная до момента выключения дви-гателя, µ – коэффициент сопротивления, имеющий размерность уско-

рения. Согласно второму закону Ньютона, при равномерном движении автопоезда выполняется равенство:

F = M.

После того, как от автопоезда отцепится прицеп, уравнения движения тягача и прицепа примут вид:

(M − m) a = F − (M − m), ma 2= − µ m.

−

Следовательно, до момента выключения двигателя прицеп будет дви-гаться равноускоренно с ускорением a = µ Mmm, а прицеп – равноза-медленно с ускорением, модуль которого | a 2 | = µ. Из кинематических уравнений движения прицепа следует, что расстояние, пройденное им до полной остановки, равно

2 2

s 2 = 2 v 02 |= v 0.

К моменту выключения двигателя тягач наберет скорость

v = v 0 +2 a s. После выключения двигателя он будет двигаться равно-

замедленно с ускорением, модуль которого | a 2 |. Поэтому при движе-нии накатом тягач пройдет путь

v v

2 2

s = 2| a 2 | = 2µ + M − m s.

−

Учитывая, что искомое расстояние L = s + s − s 2, получаем ответ: L = Msm = 500 м.

I.3. Вычислим силу натяжения стержня в том его сечении, которое находится на границе между гладкой и шероховатой частями наклонной

Решения задач

поверхности клина. Пусть полная масса стержня равна m. Рассмотрим момент, когда на гладкой части клина окажется нижняя часть стержня массой b m, а на шероховатой части клина – верхняя часть стержня

массой (1−) m, причем значения коэффициента лежат в диапазоне 0 £ b £ 1. Уравнения движения нижней и верхней частей стержня имеют

вид:

b ma =b mg sina − T,

(1− b) ma = (1−) mg sina + T − (1−) mg cosa,

где a – ускорение стержня, g – ускорение свободного падения, T –

сила взаимодействия нижней и верхней частей стержня (сила натяжения стержня) в рассматриваемый момент. Решая эту систему, находим

T =b(1− b)µ mg cosa.

Видно, что сила натяжения стержня в сечении, которое находится на границе между гладкой и шероховатой частями клина, зависит от зна-чения коэффициента b. Очевидно, она будет максимальной при

= 0, 5, т.е. когда одна половина стержня окажется на гладкой нижней

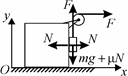части клина, а другая половина – на его шероховатой верхней части. Проводя аналогичные рассуждения, нетрудно установить, что сила на-тяжения стержня будет линейно убывать с расстоянием от сечения стержня, совпадающего с границей между гладкой и шероховатой час-тями клина. Предлагаем самостоятельно убедиться в этом. Следова-тельно, T ax= 1µ mg cosa.

*I.4. Когда кубик и груз освободят, они придут в движение под дей-ствием сил, модули и направления которых

указаны на рис. 91. Здесь mg и µ N – модули

силы тяжести и силы трения скольжения, дей-ствующих на груз, N – модуль нормальной

составляющей силы взаимодействия кубика и груза, F – модуль силы натяжения нити, рав-ный модулю заданной в условии силы, прило-

Рис. 91

Физический факультет

женной к свободному концу нити. Полагая, что система отсчета, свя-занная со столом, является инерциальной, запишем уравнения движения кубика и груза в проекциях на координатные оси Ox и Oy:

Max = F − N, max = N, may = F − mg − N,

где ax – модуль ускорения кубика, равный модулю горизонтальной составляющей ускорения груза, ay – модуль вертикальной составляю-щей ускорения груза. Из этих уравнений находим

ax = MFm,

M +(1−) m y (M + m) m

Пусть за время t перемещение кубика составило ∆ x, а груз поднялся на высоту ∆ y. Поскольку движение этих тел начинается из состояния

∆

y a

покоя, то ∆ x = ax t, ∆ y = ay t. Следовательно, ∆ x = ax. Перемеще- y

ние свободного конца нити относительно неподвижной системы отсчета при этом равно ∆ x +∆ y. Работа, которую совершает сила,

∆

A = F (x +∆ y)= F ∆ x æ 1+ ay ö. è x ø

Объединяя записанные выражения, получаем ответ:

∆ x = (2− µ+(M

m)) F − (m + M) g

()

m + M mg

Анализ этого выражения показывает, что оно теряет смысл при

F £ F = M + m (− µ). Таким образом, найденное решение существует, если F > F.

I.5. Рассмотрим движение груза после того, как нить, на которой он подвешен, зацепится за нижний гвоздь. В верхней точке окружности, по которой движется груз, на него действуют сила тяжести и сила натяже-

Решения задач

ния нити (см. рис. 92). Обозначив через mg и T модули этих сил, по второму закону Ньютона имеем:

mv 2= mg + T,

где v – скорость груза в верхней точке, R – радиус окружности. Отсю-да следует, что груз совершает на нити полный

оборот по окружности, если v 2³ gR. Обозначив

через v 0скорость груза в нижней точке, по закону сохранения механической энергии имеем:

2 2

mv 2= mv 2+ 2 mgR. Рис. 92 Отсюда v 2= v 2+ 4 gR. С учетом найденного выше условия для скоро-

сти груза в верхней точке находим, что R £ 5 g. Таким образом, макси-

мальное значение радиуса, при котором груз совершит полный оборот по окружности, равно

2 R max = 5 g.

Применяя для движения груза от исходного положения до нижней точ-ки закон сохранения механической энергии, получаем, что v 2 = 2 gL.

Следовательно, R max = 2 L, и максимальная высота, на которую под-

нимется груз

h max = 2 R max = 4 L.

Чтобы эта высота была достигнута, нужно вбить нижний гвоздь на рас-стоянии x = x 0 = L − R max = 3 L от верхнего. Если вбить гвоздь ниже

найденной точки (при этом x > x 0), то радиус окружности, по которой

Физический факультет

движется груз, будет меньше R max, и груз достигнет в верхней точке окружности высоты, меньшей чем h max. Если же вбить гвоздь выше найденной точки (при этом x < x 0), то натяжение нити обратится в нуль, т.е. нить провиснет, когда груз еще не достигнет верхней точки. В

этом случае траектория груза кроме дуги окружности будет включать в себя отрезок параболы. Таким образом, ответ имеет вид: x = 0, 6 L.

∆

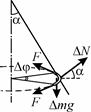
I.6. Выделим малый элемент кольца массой ∆ m = m 2p, где ∆ < < 1. Этот элемент находится в равновесии под

действием сил, модули и направления которых изо-бражены на рис. 93, где ∆ mg – модуль силы тяжести,

∆ N – модуль силы реакции поверхности конуса, F – модуль силы натяжения кольца. Векторная сумма сил натяжения, действующих на выделенный элемент со стороны соседних участков кольца, направлена к цен-

Рис. 93 тру кольца и по модулю равна ∆ F = 2 F sin ∆ f» F ∆ f.

Условия равновесия элемента кольца имеют вид:

∆ mg = ∆ N sina, F ∆ f = ∆ N cosa.

∆ mg mg

2 F

Отсюда tga= F ∆ f =2p F. Полагая, что F – максимально допустимое натяжение кольца, получаем ответ: amin = arctg mg.

I.7. Цилиндр и доски находятся в равновесии под действием сил, модули и направления которых изображены на рис. 94, где Mg и mg –

модули сил тяжести, действующих на цилиндр и на каждую из досок, N – модуль нормальной составляющей силы взаимодействия каждой из досок и цилиндра, F тр – модуль силы трения покоя между цилин-

дром и каждой из досок. Силы реакции оси, на которой подвешены дос-

Решения задач

ки, на рисунке не показаны. Для облегчения анализа рисунка в левой его части изображены силы, действующие только на

цилиндр, а в правой – только на правую доску. Уравнение моментов сил, действующих на одну из досок, записанное относительно точки O, имеет вид:

2 2

mg L sina = N L.

Цилиндр находится в равновесии при выполнении

условия: Рис. 94

Mg + 2 N sina = 2 F р cosa.

Из записанных уравнений находим, что

N = mg sina,

Mg + 2 mg sin2 a тр 2cosa

Сила трения покоя удовлетворяет неравенству: F р £ µ N. Следователь-

но, система будет находиться в равновесии при условии, что µ ³ тр.

Учитывая, что sina = R, cosa =

R 2 +(L /2)2

L /2, получаем

R 2 +(L /2)2

2 2

R L

ответ: µ ³ (L 4 mRLM + 2 R.

I.8. Согласно формуле Гюйгенса, период колебаний математическо-го маятника длиной l равен

T = 2p l,

где g – ускорение свободного падения в той области вблизи поверхно-

сти планеты, где расположен маятник. В частности, на полюсе ускоре-ние свободного падения g п целиком определяется силой гравитацион-ного притяжения тела к планете. По закону всемирного тяготения

Физический факультет

g п = G M,

где G» 6, 67× 10− 11 м3/(кг·с2) – гравитационная постоянная, M – масса

планеты, R – ее радиус. Тело, находящееся на экваторе, движется отно-сительно инерциальной системы, связанной с центром планеты, по ок-ружности радиусом R. По второму закону Ньютона для тела массой m, покоящегося на экваторе, имеем:

m w2 R = mg п − N,

где w – угловая скорость вращения планеты, N – модуль силы реакции опоры. Отсюда находим, что сила, с которой тело, находящееся на эква-торе, давит на опору, N = m (g п − w2 R). Следовательно, предоставлен-ное самому себе тело будет совершать на экваторе свободное падение с ускорением g э = g п − w 2 R. По условию период колебаний маятника на экваторе э связан с периодом колебаний на полюсе п соотношением:

э п

T = nT. Поэтому g п = n 2 g э, откуда

w = 1 g п (n 2 − 1).

Учитывая, что масса планеты M = 4p R r, а искомый период вращения

планеты вокруг ее оси t= 2p, после несложных преобразований нахо-

дим ответ: t= n G r(n 2− 1)» 2, 5 часа.

1 1

I.9. Поскольку грузы смещают от положений равновесия на одина-ковые расстояния, центр масс системы, совпадающий с центром тре-угольника (точкой O) остается неподвижным. Пусть смещение каждого груза равно. Из рис. 95 видно, что удлинение любой из трех пружин составит при этом величину ∆ x = 2 x, где x = x cos30°. По закону Гука

сила упругости, возникающая при растяжении пружины, равна по мо-

Решения задач

дулю F = k ∆ x. На каждый груз действуют две такие силы, направлен-ные под углом 60° друг к другу. Их векторная

сумма направлена к центру треугольника и по модулю равна 2 F cos30°. Объединяя записан-ные выражения, находим, что возвращающие силы, возникающие при смещении грузов на расстояние x, равны по модулю 3 kx. Поэтому уравнение движения каждого из грузов имеет

вид: Рис. 95

m & & = − 3 k x.

Следовательно, w2= 3 k. Учитывая, что период колебаний T = 2p, по-

лучаем ответ: T = 2p m.

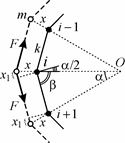I.10. Поскольку грузы смещают от положений равновесия на одина-ковые расстояния, центр масс системы, совпа-

дающий с центром n -угольника (точкой O) ос-тается неподвижным. Пусть смещение каждого груза равно x. Из рис. 96 видно, что удлинение любой из n пружин составит при этом величи-ну ∆ x = 2 x, где x = x sin a, а a = 2pПо за-

кону Гука сила упругости, возникающая при растяжении пружины, равна по модулю F = k ∆ x. На каждый груз действуют две такие силы, направленные под углом 2 друг к другу,

Рис. 96

2 2

где b = p− a. Их векторная сумма направлена к центру n -угольника и

æ ö

ç ÷

2 2 2

по модулю равна 2 F cosb = 2 F cosè p− aø = 2 F sin a. Объединяя запи-санные выражения, находим, что возвращающие силы, возникающие

Физический факультет

æ ö

ç ÷

при смещении грузов на расстояние x, равны по модулю è 4 k sin2 2 ø x. Поэтому уравнение движения каждого из грузов имеет вид:

& &

ç ÷

è ø

mx = − æ 4 k sin2 aö x.

Следовательно, w 2 = 4 k sin2 a. Учитывая, что период колебаний

T = 2p, получаем ответ: T = sin(p/ n) m.

⇐ Предыдущая 16 17 18 19 202122 23 24 25 Следующая ⇒

© 2023 :: MyLektsii.ru :: Мои Лекции
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав.
Копирование текстов разрешено только с указанием индексируемой ссылки на источник.