
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Упрощение матричных игр
|
|
Решение матричных игр тем сложнее, чем больше размерность платёжной матрицы. Поэтому для игр с платёжными матрицами большой размерности отыскание оптимального решения можно упростить, если уменьшить их размерность путём исключения дублирующих и заведомо невыгодных (доминируемых) стратегий.
Определение 1. Если в платёжной матрице игры все элементы строки (столбца) равны соответствующим элементам другой строки (столбца), то соответствующее этим строкам (столбцам) стратегии называются дублирующими.
Определение 2. Если в платёжной матрице игры все элементы некоторой строки, определяющей стратегию Аi игрока А, не больше (меньше или некоторые равны) соответствующих элементов другой строки, то стратегия Аi называется доминируемой (заведомо невыгодной).
Определение 3. Если в платёжной матрице игры все элементы некоторого столбца, определяющего стратегию Вi игрока В не меньше (больше или некоторые равны) соответствующих элементов другого столбца, то стратегия Вi называется доминируемой (заведомо невыгодной).
Правило. Решение матричной игры не изменится, если из платёжной матрицы исключить строки и столбцы, соответствующие доминируемым стратегиям и одной из каждой пары дублирующих стратегий.
Пример. Упростить матричную игру, платёжная матрица которой имеет вид:
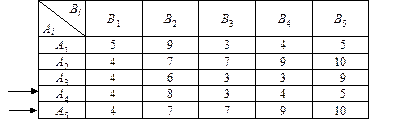
Из платёжной матрицы видно, что стратегия А 2 дублирует стратегию А 5, потому любую из них можно отбросить (отбросим стратегию А 5). Сравнивая почленно стратегии А 1 и А 4, видим, что каждый элемент строки А 4 не больше соответствующего элемента строки А 1. Поэтому применение игроком А доминирующей над А 4 стратегии А 1 всегда обеспечивает выигрыш, не меньший того, который был бы получен при применении стратегии А 4. Следовательно, стратегию А 4 можно отбросить. Таким образом, имеем упрощенную матричную игру с платёжной матрицей вида

Из этой матрицы видно, что в ней некоторые стратегии игрока В доминируют над другими: В 3 над В 2, В 4 и В 5. Отбрасывая доминируемые стратегии В 2, В 4 и В 5, получаем игру 3´ 2, имеющей платёжную матрицу вида

В этой матрице стратегия А 3 доминируется как стратегией А 1, так и стратегией А 2. Отбрасывая стратегию А 3, окончательно получаем игру 2´ 2 с платёжной матрицей

Эту игру уже упростить нельзя, её надо решать рассмотренными выше алгебраическим или геометрическим методами.
Необходимо отметить, что, отбрасывая дублируемые и доминируемые стратегии в игре с седловой точкой, мы все равно придем к игре с седловой точкой, т.е. к решению в чистых стратегиях. Но лучше сразу проверить, не обладает ли игра седловой точкой – это проще, чем сравнивать почленно все строки и все столбцы платёжной матрицы.
Алгебраические методы решения матричных игр иногда производить проще, если использовать также следующие свойства матричных игр.
Свойство 1. Если ко всем элементам платёжной матрицы прибавить (вычесть) одно и то же число С, то оптимальные смешанные стратегии игроков не изменятся, а только цена игры увеличится (уменьшится) на это число С.
Свойство 2. Если каждый элемент платёжной матрицы умножить на положительное число k, то оптимальные смешанные стратегии игроков не изменятся, а цена игры увеличится в k раз.
Эти два свойства матричных игр применяются в следующих случаях:
1) если матрица игры наряду с положительными имеет и отрицательные элементы, то ко всем её элементам прибавляют такое число, чтобы исключить отрицательные числа в матрице;
2) если матрица игры имеет дробные числа, то для удобства вычислений элементы этой матрицы следует умножить на такое число, чтобы все выигрыши были целыми числами.
Пример. Решить матричную игру 2´ 2 с платёжной матрицей вида:

Умножая все элементы платёжной матрицы на 10, а затем прибавляя к ним число 2, получаем игру с платёжной матрицей

Решая эту игру алгебраическим методом, получаем
 ;
;  ;
;
 ;
;  ;
;
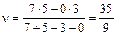 .
.
В соответствии со свойствами 1 и 2, исходная матричная игра имеет те же оптимальные смешанные стратегии:  и
и 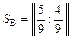 . А для получения исходной цены игры необходимо из полученной цены игры вычесть 2, а затем разделить на 10. Таким образом, получаем цену исходной игры:
. А для получения исходной цены игры необходимо из полученной цены игры вычесть 2, а затем разделить на 10. Таким образом, получаем цену исходной игры: 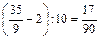 .
.
3.3.7. Решение игр 2´ n и m´ 2
Как уже отмечалось в теореме об активных стратегиях, любая конечная игра m ´ n имеет решение, в котором число активных стратегий каждого игрока не превосходит  , где
, где  . Следовательно, у игры 2´ n или m ´ 2 всегда имеется оптимальное решение содержащее не более двух
. Следовательно, у игры 2´ n или m ´ 2 всегда имеется оптимальное решение содержащее не более двух
активных стратегий у каждого из игроков 
=  . Если эти активные стратегии игроков будут найдены, то игры 2´ n и m ´ 2 превращаются в игры 2´ 2, методы решения которых рассмотрены выше.
. Если эти активные стратегии игроков будут найдены, то игры 2´ n и m ´ 2 превращаются в игры 2´ 2, методы решения которых рассмотрены выше.
Практически решение игры 2´ n осуществляется следующим образом:
1) строится графическое изображение игры для игрока А;
2) выделяется нижняя граница выигрыша и находится наибольшая ордината нижней границы (максимин), которая равна цене игры n;
3) определяется пара стратегий игрока В, пересекающихся в точке оптимума. Эти стратегии и являются активными стратегиями игрока В.
Таким образом, игра 2´ n сведена к игре 2´ 2, которую более точно можно решить алгебраическим методом.
Если в точке оптимума пересекается более двух стратегий, то в качестве активных стратегий может быть выбрана любая пара из них.
Решение игры m ´ 2 осуществляется аналогично. Но в этом случае строится графическое изображение игры для игрока В и выделяется не нижняя, а верхняя граница выигрыша (так как находится оптимальная смешанная стратегия игрока В), и на ней находится точка оптимума с наименьшей ординатой (минимакс).
Пример. Найти решение игры, платёжная матрица которой имеет вид:

Платёжная матрица не имеет седловой точки, поэтому оптимальное решение должно быть в смешанных стратегиях. Строим графическое изображение игры для игрока А (рис.3.11).
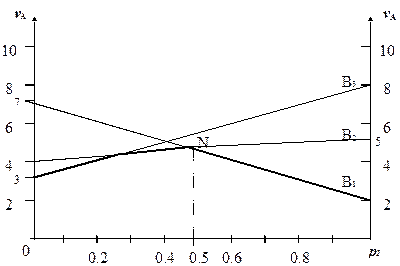
Рис. 3.11. Графическое изображение игры для игрока А
Точка N (максимин) является точкой оптимума. В этой точке пересекаются линии, соответствующие активным стратегиям B 1 и B 2 игрока B.
Таким образом, исключая стратегию B 3, получаем матричную игру 2x2 с платёжной матрицей вида

Используя алгебраический метод решения этой игры, получаем точное решение
 ;
;  ;
;
 ;
; 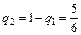 ;
;
 .
.
Ответ: 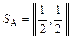 ;
;  ;
;  .
.
Пример. Найти решение игры, платёжная матрица которой имеет вид
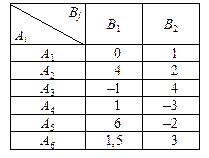
Платёжная матрица не имеет седловой точки. Для сведения данной игры к игре 2´ 2 строим её графическое изображение для игрока В (рис. 3.12).

Рис.3.12. Графическое изображение игры для игрока В
Точка М (минимакс) является точкой оптимума. В этой точке пересекаются отрезки, соответствующие активным стратегиям А 2, А 6 и А 3 игрока А. Таким образом, исключая стратегии А 1, А 4 и А 5 и выбирая из трех активных стратегий две (например, А 2 и А 3 или А 2 и А 6), приходим к матричной игре 2´ 2. Выбор стратегий А 3 и А 6 исключен, так как в этом случае точка М перестанет быть точкой минимакса.
Пусть выбираются стратегии А 2 и А 3. Тогда игра 2´ 2 приобретает вид

Оптимальные смешанные стратегии данной игры, а, следовательно, и исходной игры определяются следующими вероятностями:
 ;
;  ;
;
 ;
;  ;
;
 .
.
Ответ:  ;
;  ;
;  .
.
Другой вариант игры 2´ 2 получается, если использовать стратегии А 2 и А 6. В этом случае платёжная матрица имеет вид

Тогда
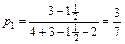 ;
; 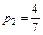 ;
;
 ;
;  ;
;
 .
.
Ответ:  ;
;  ;
;  .
.
Естественно, что цена игры для обоих вариантов способов решения задачи одинакова.
В заключение наметим общую схему решения матричных игр 2´ n и m ´ 2:
1. Определяется наличие седловой точки, т.е. возможность решения игры в чистых стратегиях. Если нижняя цена игры a не равна верхней цене игры b, то осуществляется поиск решения в смешанных стратегиях.
2. Производится упрощение матричной игры путем исключения дублирующих и доминируемых стратегий. Если упрощенная игра имеет размерность не 2´ 2, то переходим к этапу 3.
3. Строится графическое изображение игры и определяется две активные стратегии игрока, имевшего в исходной задаче число стратегий больше двух.
4. Решается матричная игра 2´ 2.
3.3.8. Решение игр m´ n. Эквивалентные задачи линейного программирования
Пусть имеется матричная игра m ´ n без седловой точки с матрицей выигрышей  . Допустим, что все выигрыши aij положительны (этого всегда можно добиться, прибавляя ко всем элементам матрицы достаточно большое число С; от этого, как уже отмечалось, цена игры увеличится на C, а оптимальные решения SA и SB не изменятся).
. Допустим, что все выигрыши aij положительны (этого всегда можно добиться, прибавляя ко всем элементам матрицы достаточно большое число С; от этого, как уже отмечалось, цена игры увеличится на C, а оптимальные решения SA и SB не изменятся).
Если все aij положительны, то и цена игры  при оптимальной стратегии тоже положительна, т.к.
при оптимальной стратегии тоже положительна, т.к.  .
.
В соответствии с основной теоремой матричных игр, если платёжная матрица не имеет седловой точки, то имеется пара оптимальных смешанных стратегий  и
и  , применение которой обеспечивает игрокам получение цены игры
, применение которой обеспечивает игрокам получение цены игры  .
.
Найдем вначале SA. Для этого предположим, что игрок В отказался от своей оптимальной смешанной стратегии SB и применяет только чистые стратегии. В каждом из этих случаев выигрыш игрока А будет не меньше, чем  :
:
 . (3.25)
. (3.25)
Разделив левую и правую часть каждого из неравенств (3.25) на положительную величину n и введя обозначения:
 , (3.26)
, (3.26)
запишем неравенства (3.25) в следующем виде:
 , (3.27)
, (3.27)
где x 1, x 2,... xm – неотрицательные переменные.
В силу того, что
 ,
,
переменные x 1, x 2,... x mудовлетворяют условию
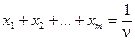 . (3.28)
. (3.28)
Учитывая, что игрок А стремится максимизировать n, получаем следующую задачу линейного программирования: найти неотрицательные значения переменных x 1, x 2,... x mтакие, чтобы они удовлетворяли линейным ограничениям – неравенствам (3.27) и обращали в минимум линейную функцию этих переменных:
 . (3.29)
. (3.29)
Из решения задачи линейного программирования находим цену игры n и оптимальную стратегию S Aпо формулам:
 , (3.30)
, (3.30)
 ,
,  . (3.31)
. (3.31)
Аналогично находим оптимальную стратегию S Bигрока В. Предположим, что игрок А отказался от своей оптимальной стратегии S Aи применяет только чистые стратегии. Тогда проигрыш игрока В в каждом из этих случаев будет не больше, чем  :
:
 . (3.32)
. (3.32)
Разделив левую и правую части каждого их неравенств (3.32) на положительную величину n и введя обозначения:
 , (3.33)
, (3.33)
запишем неравенство (2.32) в следующем виде:
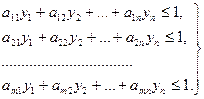 , (3.34)
, (3.34)
где y 1, y 2,..., yn – неотрицательные переменные.
В силу того, что  , переменные y 1, y 2,..., y nудовлетворяют условию
, переменные y 1, y 2,..., y nудовлетворяют условию
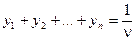 . (3.35)
. (3.35)
Учитывая, что игрок В стремится минимизировать положительную цену n (свой проигрыш), получаем задачу линейного программирования: найти неотрицательные значения переменных y 1, y 2,..., yn такие, чтобы они удовлетворяли линейным ограничениям (3.34) и обращали в максимум линейную функцию этих переменных:
 . (3.36)
. (3.36)
Эта задача является двойственной по отношению к задаче, представленной условиями (3.27) и (3.29).
Оптимальная стратегия  игрока В определяется из решения двойственной задачи линейного программирования по формулам:
игрока В определяется из решения двойственной задачи линейного программирования по формулам:
 ,
,  . (3.37)
. (3.37)
Так как игрок А стремится получить цену игры n как можно большую,  должна быть минимизирована.
должна быть минимизирована.
Таким образом, оптимальные стратегии  и
и  матричной игры m ´ n с платёжной матрицей
матричной игры m ´ n с платёжной матрицей  могут быть найдены путем решения пары двойственных задач линейного программирования:
могут быть найдены путем решения пары двойственных задач линейного программирования:
| Прямая (исходная) задача | Двойственная задача |
 , ,
 , ,  ; ;
 , , 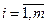 . .
|  , ,
 , , 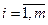 ; ;
 , ,  . .
|
При этом
 , (3.38)
, (3.38)

Пример. Найти решение и цену матричной игры, платёжная матрица которой имеет вид

|
|