Эпилог: смерть звезд

Умирая, многие звезды заканчивают свой путь в качестве сверхплотных шаров ядерной материи, переплетенной с множеством электронов. Это так называемые белые карлики. Такой будет и судьба нашего Солнца, когда оно примерно через 5 миллиардов лет исчерпает запасы ядерного топлива, и судьба еще более 95 % звезд нашей Галактики. Пользуясь только ручкой, бумагой и немного головой, можно вычислить наибольшую возможную массу таких звезд. Эти вычисления, впервые предпринятые в 1930 году Субраманьяном Чандрасекаром, с помощью квантовой теории и теории относительности позволили сделать два ясных прогноза. Во‑ первых, это было предсказание самого существования белых карликов – шариков материи, которые, по принципу Паули, спасает от разрушения сила собственной гравитации. Во‑ вторых – если мы отвлечемся от листка бумаги со всякими теоретическими каракулями и посмотрим в ночное небо, мы никогда не увидим белый карлик с массой, которая бы более чем в 1, 4 раза превосходила массу нашего Солнца. Оба этих предположения отличаются невероятной дерзостью.

Сегодня астрономы уже занесли в каталоги около 10 000 белых карликов. У большинства из них масса составляет примерно 0, 6 массы Солнца, а самая большая зафиксированная – немногим менее 1, 4 массы Солнца. Это число – 1, 4 – свидетельство триумфа научного метода. Оно опирается на понимание ядерной физики, квантовой физики и специальной теории относительности Эйнштейна – трех китов физики XX века. При его вычислении требуются также фундаментальные константы природы, с которыми мы уже встречались в этой книге. К концу эпилога мы выясним, что максимальная масса определяется отношением

Смотрите внимательно на то, что мы записали: результат зависит от постоянной Планка, скорости света, гравитационной постоянной Ньютона и массы протона. Удивительно, что мы можем предсказать наибольшую массу умирающей звезды с помощью сочетания фундаментальных констант. Трехстороннее сочетание гравитации, относительности и кванта действия, появляющееся в уравнении (hc / G)½, называется планковской массой, и при подстановке цифр оказывается, что она равна примерно 55 мкг, то есть массе песчинки. Поэтому, как ни странно, предел Чандрасекара вычисляется с помощью двух масс – песчинки и протона. Из таких ничтожных величин образуется новая фундаментальная единица массы Вселенной – масса умирающей звезды. Мы можем довольно долго объяснять, как получается предел Чандрасекара, но вместо этого пойдем немного дальше: мы опишем собственно вычисления, потому что они и есть самая интригующая часть процесса. У нас не получится точного результата (1, 4 массы Солнца), но мы приблизимся к нему и увидим, как профессиональные физики делают глубокие выводы с помощью последовательности тщательно продуманных логических ходов, постоянно обращаясь при этом к хорошо известным физическим принципам. Ни в один из моментов вам не придется верить нам на слово. Сохраняя холодную голову, мы будем медленно и неотвратимо приближаться к совершенно поразительным заключениям.

Начнем с вопроса: что такое звезда? Можно почти без ошибки сказать, что видимая Вселенная состоит из водорода и гелия – двух самых простых элементов, сформированных в первые несколько минут после Большого взрыва. После примерно полумиллиарда лет расширения Вселенная стала достаточно холодной, чтобы более плотные области в газовых облаках под действием собственной гравитации стали собираться вместе. Это были первые зачатки галактик, и внутри них, вокруг более мелких «комков», начали формироваться первые звезды.

Газ в этих прототипах звезд, по мере того как они коллапсировали, становился все горячее, что известно любому обладателю велосипедного насоса: при сжатии газ нагревается. Когда газ достигает температуры около 100 000 ℃, электроны больше не могут удерживаться на орбитах вокруг ядер водорода и гелия, и атомы распадаются, образуя горячую плазму, состоящую из ядер и электронов. Горячий газ пытается расшириться, противодействуя дальнейшему схлопыванию, но при достаточной массе гравитация одерживает верх.

Так как протоны имеют положительный электрический заряд, они будут взаимно отталкиваться. Но гравитационный коллапс набирает силу, температура продолжает повышаться, и протоны начинают двигаться все быстрее. Со временем при температуре в несколько миллионов градусов протоны будут двигаться максимально быстро и приблизятся друг к другу так, что слабое ядерное взаимодействие возобладает. Когда это произойдет, два протона смогут вступить в реакцию друг с другом: один из них спонтанно становится нейтроном, одновременно испуская позитрон и нейтрино (точно так, как показано на рис. 11.3). Освободившись от силы электрического отталкивания, протон и нейтрон сливаются в результате сильного ядерного взаимодействия, образуя дейтрон. При этом высвобождается огромное количество энергии, поскольку, как и в случае с образованием молекулы водорода, связывание чего‑ то вместе высвобождает энергию.

При одном слиянии протонов высвобождается совсем мало энергии по повседневным стандартам. Один миллион слияний пар протонов дает энергию, равную кинетической энергии комара в полете или энергии излучения 100‑ ваттной лампочки за наносекунду. Но в атомарном масштабе это гигантское количество; кроме того, помните, что мы говорим о плотном ядре сжимающегося газового облака, в котором количество протонов на 1 см³ достигает 1026. Если все протоны в кубическом сантиметре сольются в дейтроны, освободится 10¹ ³ джоулей энергии – достаточно для обеспечения годовой потребности небольшого города.

Слияние двух протонов в дейтрон – начало самого разнузданного синтеза. Сам этот дейтрон ищет возможности слиться с третьим протоном, образуя более легкий изотоп гелия (гелий‑ 3) и испуская фотон, а эти ядра гелия затем порождают пару и сливаются в обычный гелий (гелий‑ 4) с испусканием двух протонов. На каждой стадии синтеза высвобождается все больше энергии. Кроме того, позитрон, появившийся в самом начале цепочки превращений, тоже быстро сливается в окружающей плазме с электроном, образуя пару фотонов. Вся эта освобожденная энергия направляется в горячий газ, состоящий из фотонов, электронов и ядер, который противостоит сжатию материи и останавливает гравитационный коллапс. Такова звезда: ядерный синтез сжигает находящееся внутри ядерное топливо, образуя внешнее давление, которое стабилизирует звезду, не давая осуществиться гравитационному коллапсу.

Разумеется, когда‑ то водородное топливо заканчивается, ведь его количество конечно. Если энергия больше не высвобождается, прекращается внешнее давление, гравитация вновь вступает в свои права, и звезда возобновляет отложенный коллапс. Если звезда достаточно массивна, ее ядро может прогреться до температуры примерно 100 000 000 ℃. На этой стадии гелий – побочный продукт сжигания водорода – воспламеняется и начинает свой синтез, образуя углерод и кислород, и гравитационный коллапс снова прекращается.

Но что происходит, если звезда недостаточно массивна, чтобы начался гелиевый синтез? Со звездами, масса которых менее половины массы нашего Солнца, случается нечто крайне удивительное. При сжатии звезда разогревается, но еще до того, как ядро достигает температуры 100 000 000 ℃, кое‑ что приостанавливает коллапс. Это кое‑ что – давление электронов, которые соблюдают принцип Паули. Как мы уже знаем, принцип Паули жизненно необходим для понимания того, как атомы остаются стабильными. Он лежит в основе свойств материи. И вот еще одно его достоинство: он объясняет существование компактных звезд, которые продолжают свое существование, хотя уже выработали все ядерное топливо. Как же это работает?

Когда звезда сжимается, электроны внутри нее начинают занимать меньший объем. Мы можем представлять электрон звезды через его импульс p, тем самым ассоциируя его с длиной волны де Бройля, h / p. Напомним, что частица может быть описана только таким волновым пакетом, который по крайней мере не меньше связанной с ней длиной волны[56]. Это значит, что если звезда достаточно плотная, то электроны должны перекрывать друг друга, то есть нельзя считать, что они описываются изолированными волновыми пакетами. Это, в свою очередь, обозначает, что для описания электронов важны эффекты квантовой механики, в особенности принцип Паули. Электроны уплотняются до тех пор, пока два электрона не начинают претендовать на занятие одной и той же позиции, а принцип Паули гласит, что электроны не могут этого делать. Таким образом, и в умирающей звезде электроны избегают друг друга, что помогает избавиться от дальнейшего гравитационного коллапса.

Такова судьба более легких звезд. А что будет с Солнцем и другими звездами подобной массы? Мы ушли от них пару абзацев назад, когда пережигали гелий в углерод и водород. Что будет, когда гелий тоже кончится? Они тоже должны будут начать сжиматься под действием собственной гравитации, то есть электроны будут уплотняться. И принцип Паули, как и в случае с более легкими звездами, в итоге вмешается и прекратит коллапс. Но для самых массивных звезд даже принцип Паули оказывается не всесилен. Когда звезда сжимается и электроны уплотняются, ядро разогревается, и электроны начинают двигаться все быстрее. В достаточно тяжелых звездах электроны приближаются к скорости света, после чего происходит нечто новое. Когда электроны начинают двигаться с такой скоростью, давление, которое электроны способны развивать для противостояния гравитации, понижается, и эту задачу они уже не способны решить. Они просто больше не могут бороться с гравитацией и останавливать коллапс. Наша задача в этой главе – рассчитать, когда это произойдет, и мы уже рассказали самое интересное. Если масса звезды в 1, 4 раза и больше превосходит массу Солнца, электроны терпят поражение, а гравитация выигрывает.

Так заканчивается обзор, который послужит основой наших вычислений. Теперь можно двигаться дальше, позабыв о ядерном синтезе, потому что горящие звезды лежат вне сферы наших интересов. Мы будем пытаться осознать, что происходит внутри мертвых звезд. Мы постараемся понять, как квантовое давление уплотнившихся электронов уравновешивает силу гравитации и как это давление уменьшается, если электроны двигаются слишком быстро. Таким образом, суть нашего исследования – противостояние гравитации и квантового давления.

Хотя все это не так важно для последующих расчетов, мы не можем все бросить на самом интересном месте. Когда массивная звезда схлопывается, у нее остаются два варианта развития событий. Если она не слишком тяжелая, то в ней продолжится сжатие протонов и электронов, пока они не синтезируются в нейтроны. Так, один протон и один электрон спонтанно превращаются в нейтрон с испусканием нейтрино, опять же благодаря слабому ядерному взаимодействию. Подобным образом звезда неумолимо превращается в небольшой нейтронный шарик. По словам русского физика Льва Ландау, звезда становится «одним гигантским ядром». Ландау написал это в своей работе 1932 года «К теории звезд», которая появилась в печати в том самом месяце, когда Джеймс Чедвик открыл нейтрон. Наверное, слишком смело было бы сказать, что Ландау предсказал существование нейтронных звезд, но он определенно что‑ то подобное предчувствовал, и с большой дальновидностью. Вероятно, приоритет следует признать за Вальтером Бааде и Фрицем Цвикки, которые в 1933 году написали: «Мы имеем все основания предполагать, что сверхновые представляют собой переход от обычных звезд к нейтронным звездам, которые на конечных этапах существования состоят из чрезвычайно плотно упакованных нейтронов».

Эта идея показалась настолько нелепой, что была спародирована в Los Angeles Times (см. рис. 12.1), и нейтронные звезды до середины 1960‑ х годов оставались теоретическим курьезом.

Рис. 12.1. Карикатура из номера газеты Los Angeles Times от 19 января 1934 года

В 1965 году Энтони Хьюиш и Сэмюэл Окойе нашли «свидетельства необычного источника яркости радиоизлучения высокой температуры в Крабовидной туманности», хотя и не смогли опознать в этом источнике нейтронную звезду. Опознание случилось в 1967 году благодаря Иосифу Шкловскому, а вскоре, после более подробных исследований, и благодаря Джоселин Белл и тому же Хьюишу. Первый пример одного из самых экзотических объектов во Вселенной получил название пульсара Хьюиша – Окойе. Интересно, что та же сверхновая, что породила пульсар Хьюиша – Окойе, была замечена астрономами за 1000 лет до этого. Великая сверхновая 1054 года, самая яркая в зафиксированной истории, наблюдалась китайскими астрономами и, как известно благодаря знаменитому наскальному рисунку, жителями каньона Чако на юго‑ западе современных США.

Мы пока еще не говорили о том, как этим нейтронам удается сопротивляться гравитации и препятствовать дальнейшему коллапсу, но, возможно, вы и сами в состоянии предположить, почему это происходит. Нейтроны (как и электроны) – рабы принципа Паули. Они тоже могут останавливать коллапс, и нейтронные звезды, как и белые карлики, – один из вариантов окончания жизни звезды. Нейтронные звезды, вообще‑ то, отступление от нашего повествования, но мы не можем не отметить, что это совершенно особенные объекты в нашей великолепной Вселенной: это звезды размером с город, настолько плотные, что чайная ложка их вещества весит как земная гора, а не распадаются они только благодаря естественной «неприязни» частиц одного спина друг к другу.

Для самых массивных звезд во Вселенной остается только одна возможность. В этих звездах даже нейтроны движутся со скоростью, близкой к скорости света. Такие звезды ждет катастрофа, потому что нейтроны не способны создавать достаточное давление, чтобы противостоять гравитации. Пока неизвестен физический механизм, не дающий ядру звезды, масса которой примерно в три раза больше массы Солнца, упасть самому на себя, и результатом становится черная дыра: место, в котором все известные нам законы физики отменяются. Предполагается, что законы природы все же продолжают действовать, но для полного понимания внутренней работы черной дыры требуется квантовая теория гравитации, которой пока не существует.

Однако пора вернуться к сути дела и сосредоточиться на нашей двоякой цели – доказательстве существования белых карликов и расчете предела Чандрасекара. Мы знаем, как поступать: необходимо уравновесить гравитацию и давление электронов. Такие вычисления нельзя сделать в уме, так что стоит наметить план действий. Итак, вот план; он довольно длинный, потому что мы хотим сначала разъяснить некоторые второстепенные детали и подготовить почву для собственно вычислений.

Шаг 1: мы должны определить, каково давление внутри звезды, оказываемое сильно сжатыми электронами. Возможно, вас заинтересует, почему мы не обращаем внимания на другие частицы внутри звезды: что насчет ядер и фотонов? Фотоны не подчиняются принципу Паули, так что со временем они все равно покинут звезду. В борьбе с гравитацией они не помощники. Что же до ядер, то ядра с полуцелым спином подчиняются принципу Паули, но (как мы увидим) из‑ за того, что их масса больше, они оказывают меньшее давление, чем электроны, и их вклад в борьбу с гравитацией можно спокойно игнорировать. Это существенно упрощает задачу: все, что нам нужно, – давление электронов. На том и успокоимся.

Шаг 2: вычислив давление электронов, мы должны заняться вопросами равновесия. Может быть непонятно, что делать дальше. Одно дело сказать, что «гравитация давит, а электроны противостоят этому давлению», совсем другое – оперировать при этом числами. Давление внутри звезды будет варьироваться: в центре оно будет больше, а на поверхности меньше. Наличие перепадов давления очень важно. Представьте себе куб из звездной материи, который находится где‑ то внутри звезды, как показано на рис. 12.2. Гравитация направит куб к центру звезды, и мы должны понять, как будет противостоять этому давление электронов. Давление электронов в газе оказывает воздействие на каждую из шести граней куба, и это воздействие будет равно давлению на грань, помноженному на площадь этой грани. Это утверждение точно. До того мы использовали слово «давление», предполагая, что обладаем достаточным интуитивным пониманием того, будто газ при высоком давлении «давит» больше, чем при низком. Собственно, это известно любому, кто хоть раз накачивал насосом сдувшуюся автомобильную шину.

Рис. 12.2. Небольшой куб где‑ то в середине звезды. Стрелки показывают силу, действующую на куб со стороны электронов в звезде

Поскольку нам нужно должным образом понять природу давления, сделаем краткую вылазку на более знакомую территорию. Обратимся к примеру с шиной. Физик сказал бы, что шина сдулась, потому что внутреннего воздушного давления недостаточно, чтобы удерживать вес автомобиля без деформации шины – за это‑ то нас, физиков, и ценят. Мы можем не ограничиться этим и вычислить, каково должно быть давление в шинах для автомобиля с массой 1500 кг, если 5 см шины должно постоянно поддерживать контакт с поверхностью, как показано на рис. 12.3: опять настало время доски, мела и тряпки.

Если ширина шины – 20 см, а длина соприкасающейся с дорогой поверхности – 5 см, то площадь поверхности шины, находящейся в непосредственном контакте с землей, будет равна 20 × 5 = 100 см³. Требуемого давления в шине мы еще не знаем – его‑ то и надо вычислить, так что обозначим его символом Р. Нам потребуется также знать действующую на дорогу силу, которую прикладывает воздух в шине. Она равна давлению, помноженному на площадь шины, контактирующую с дорогой, то есть P × 100 см². Мы должны умножить это еще на 4, поскольку у автомобиля, как известно, четыре шины: P × 400 см². Такова общая сила воздуха в шинах, действующая на поверхность дороги. Представьте ее так: молекула воздуха внутри шины молотят по земле (если быть совсем уж точными, то молотят они по резине шины, которая контактирует с землей, но это не так важно).

Земля обычно при этом не проваливается, то есть реагирует с равной, но противоположной силой (ура, наконец‑ то нам пригодился третий закон Ньютона). Машину приподнимает земля и опускает гравитация, и, поскольку при этом она не проваливается в землю и не воспаряет в воздух, мы понимаем, что эти две силы должны уравновешивать друг друга. Таким образом, можно считать, что сила P × 400 см² уравновешивается прижимной силой гравитации. Эта сила равна весу автомобиля, и мы знаем, как вычислить его с помощью второго закона Ньютона F = ma, где a – ускорение свободного падения на поверхности Земли, которое равно 9, 81 м/с². Итак, вес составляет 1500 кг × 9, 8 м/с² = 14 700 Н (ньютонов: 1 ньютон – это примерно 1 кг·м/с², что приблизительно равно весу яблока). Так как две силы равны, то

P × 400 см² = 14 700 Н.

Решить это уравнение легко: P = (14 700 / 400) Н/см² = 36, 75 Н/см². Давление в 36, 75 H на см² – возможно, не вполне знакомый нам способ выражения давления в шинах, но его можно легко преобразовать в более привычные «бары».

Рис. 12.3. Шина немного деформируется под весом автомобиля

Один бар – это стандартное давление воздуха, которое равно 101 000 Н на м². В 1 м² 10 000 см², так что 101 000 Н на м² – это 10, 1 Н на см². Таким образом, наше желаемое давление в шинах равняется 36, 75 / 10, 1 = 3, 6 бар (или 52 фунта на квадратный дюйм – это вы можете вычислить самостоятельно). С помощью нашего уравнения можно также понять, что если давление в шинах падает на 50 % до 1, 8 бар, то мы удваиваем площадь шины, находящуюся в контакте с поверхностью дороги, то есть шина немного сдувается. После этого освежающего экскурса в вычисление давления мы готовы вернуться к кубику звездной материи, который показан на рис. 12.2.

Если нижняя грань куба ближе к центру звезды, то давление на нее должно быть немного больше, чем давление на верхнюю грань. Такая разность давлений порождает действующую на куб силу, которая стремится оттолкнуть его от центра звезды («вверх» на рисунке), чего мы и хотим добиться, потому что куб в то же самое время гравитацией подталкивается к центру звезды («вниз» на рисунке). Если бы мы могли понять, как сочетать две эти силы, то улучшили бы свои представления о звезде. Но это легче сказать, чем сделать, потому что, хотя шаг 1 позволяет нам понять, каково давление электронов на куб, все еще предстоит рассчитать, насколько велико давление гравитации в противоположном направлении. Кстати, нет нужды учитывать давление на боковые грани куба, потому что они равно удалены от центра звезды, так что давление на левую сторону уравновесит давление на правую, и куб не будет двигаться ни направо, ни налево.

Чтобы выяснить, с какой силой гравитация действует на куб, мы должны вернуться к закону притяжения Ньютона, который говорит, что каждый кусочек звездной материи действует на наш кубик с силой, уменьшающейся с увеличением расстояния, то есть более далекие куски материи давят меньше, чем близкие. Кажется, тот факт, что гравитационное давление на наш куб различно для различных кусков звездной материи в зависимости от их удаленности, представляет собой сложную проблему, но мы увидим, как обойти этот момент, по крайней мере, в принципе: мы нарежем звезду на кусочки и затем вычислим силу, которую оказывает на наш куб каждый такой кусочек. К счастью, нет необходимости представлять кулинарную нарезку звезды, потому что можно использовать отличный обходной маневр. Закон Гаусса (названный в часть легендарного немецкого математика Карла Гаусса) сообщает, что: а) можно полностью игнорировать притяжение всех кусочков, находящихся дальше от центра звезды, чем наш кубик; б) общее гравитационное давление всех кусочков, находящихся ближе к центру, в точности равно давлению, которое оказывали бы эти кусочки, если бы находились ровно в центре звезды. С помощью закона Гаусса и закона притяжения Ньютона можно сделать вывод, что к кубику прикладывается сила, которая толкает его к центру звезды, и что эта сила равна

где Min – масса звезды внутри сферы, радиус которой равен расстоянию от центра до куба, Mcube – масса куба, а r – расстояние от куба до центра звезды (G – константа Ньютона). Например, если куб находится на поверхности звезды, то Min – это общая масса звезды. Для всех остальных местоположений Min будет меньше.

Мы добились определенных успехов, потому что для уравновешивания действий, оказываемых на куб (напомним, это значит, что куб не движется, а звезда не взрывается и не коллапсирует[57]), требуется, чтобы

где Pbottom и Ptop – давление электронов газа на нижней и верхней гранях куба соответственно, а А – площадь каждой стороны куба (помните, что сила, оказываемая давлением, равна давлению, умноженному на площадь). Мы отметили это уравнение цифрой (1), потому что оно очень важно и мы к нему еще вернемся.

Шаг 3: сделайте себе чаю и наслаждайтесь собой, потому что, сделав шаг 1, мы вычислили давления Pbottom и Ptop, а после шага 2 стало понятно, как именно уравновесить силы. Однако основная работа еще впереди, потому что нам нужно закончить шаг 1 и определить разницу давлений, фигурирующую в левой части уравнения (1). Это и будет нашей следующей задачей.

Представьте звезду, наполненную электронами и другими частицами. Как рассеяны эти электроны? Обратим внимание на «типичный» электрон. Мы знаем, что электроны подчиняются принципу Паули, то есть два электрона не могут находиться в одной и той же области пространства. Что это значит для того моря электронов, которое мы называем «электронами газа» в нашей звезде? Так как очевидно, что электроны отделены друг от друга, можно предположить, что каждый находится в своем миниатюрном воображаемом кубике внутри звезды. Вообще‑ то это не совсем верно, потому что мы знаем, что электроны делятся на два типа – «со спином вверх» и «со спином вниз», а принцип Паули запрещает только слишком близкое расположение идентичных частиц, то есть теоретически в кубике могут находиться и два электрона. Это контрастирует с ситуацией, которая возникла бы, если бы электроны не подчинялись принципу Паули. В этом случае они не сидели бы по двое внутри «виртуальных контейнеров». Они бы распространялись и пользовались гораздо большим жизненным пространством. Собственно, если бы можно было игнорировать различные способы взаимодействия электронов друг с другом и с другими частицами в звезде, их жизненному пространству не было бы предела. Мы знаем, что происходит, когда мы ограничиваем квантовую частицу: она совершает скачок в соответствии с принципом неопределенности Гейзенберга, и чем больше она ограничена, тем больше совершает скачков. Это значит, что, когда наш белый карлик коллапсирует, электроны все более ограничиваются и становятся все более возбужденными. Именно давление, вызванное их возбуждением, и останавливает гравитационный коллапс.

Мы можем зайти еще дальше, потому что можно применить принцип неопределенности Гейзенберга для вычисления типичного импульса электрона. Например, если мы ограничиваем электрон областью размера Δ x, он будет совершать скачки с типичным импульсом p ~ h / Δ x. Собственно, как мы говорили в главе 4, импульс приблизится к верхнему пределу, а типичный импульс будет равняться чему‑ то от нуля до этого значения; запомните эту информацию, она понадобится нам позже. Знание импульса позволяет немедленно узнать еще две вещи. Во‑ первых, если электроны не подчиняются принципу Паули, то они будут ограничены областью не размера Δ x, а гораздо большего размера. Это, в свою очередь, означает гораздо меньшее количество колебаний, а чем меньше колебаний, тем меньше давление. Итак, очевидно, что принцип Паули входит в игру; он настолько давит на электроны, что те, в соответствии с принципом неопределенности Гейзенберга, демонстрируют избыточные колебания. Через некоторое время мы преобразуем идею избыточных колебаний в формулу давления, но сначала узнаем, что же будет «во‑ вторых». Так как импульс p = mv, то скорость колебаний тоже имеет обратную зависимость от массы, так что электроны прыгают туда‑ сюда гораздо быстрее, чем более тяжелые ядра, которые тоже часть звезды. Вот почему давление атомных ядер пренебрежимо мало.

Итак, как можно, зная импульс электрона, вычислить давление, которое оказывает состоящий из этих электронов газ? Для начала нужно выяснить, какого размера должны быть блоки, содержащие пары электронов. Наши маленькие блоки имеют объем (Δ x)³, и, поскольку мы должны разместить все электроны внутри звезды, выразить это можно в виде числа электронов внутри звезды (N), деленного на объем звезды (V). Чтобы поместились все электроны, понадобится ровно N / 2 контейнеров, поскольку в каждом контейнере может располагаться два электрона. Это значит, что каждый контейнер будет занимать объем V, деленный на N / 2, то есть 2(V / N). Нам неоднократно понадобится величина N / V (количество электронов на единицу объема внутри звезды), так что присвоим ей собственный символ n. Теперь можно записать, каким должен быть объем контейнеров, чтобы в нем поместились все электроны звезды, то есть (Δ x)³ = 2 / n. Извлечение кубического корня из правой части уравнения дает возможность вывести, что

Теперь можно соотнести это с нашим выражением, полученным из принципа неопределенности, и вычислить типичный импульс электронов в соответствии с их квантовыми колебаниями:

p ~ h (n / 2)⅓, (2)

где знак ~ означает «примерно равно». Разумеется, уравнение не может быть точным, потому что все электроны никак не могут колебаться одинаково: одни будут двигаться быстрее типичного значения, другие медленнее. Принцип неопределенности Гейзенберга не способен точно сказать, сколько электронов движутся с одной скоростью, а сколько с другой. Он дает возможность сделать более приблизительное утверждение: например, если сжать область электрона, то он будет колебаться с импульсом, примерно равным h / Δ x. Мы возьмем этот типичный импульс и положим его одинаковым для всех электронов. Тем самым немного потеряем в точности вычислений, но существенно выиграем в простоте, а физика явления определенно останется той же самой[58].

Теперь мы знаем скорость электронов, что дает достаточно информации для определения давления, которое они оказывают на наш кубик. Чтобы убедиться в этом, представьте, как целый флот электронов движется в одном и том же направлении с одной и той же скоростью (v) по направлению к прямому зеркалу. Они ударяются о зеркало и отскакивают, двигаясь все с той же скоростью, но на сей раз в обратном направлении. Давайте вычислим силу, с которой электроны действуют на зеркало. После этого можно перейти к более реалистичным вычислениям для случаев, когда электроны двигаются в разных направлениях. Такая методология очень распространена в физике: сначала стоит поразмыслить над более простым вариантом задачи, которую хочешь решить. Тем самым можно разобраться в физике явления с меньшими проблемами и обрести уверенность для решения более серьезной задачи.

Представьте, что флот электронов состоит из n частиц на м³ и для простоты имеет в круглом сечении площадь 1 м², как показано на рис. 12.4. Через секунду nv электронов ударится о зеркало (если v измеряется в метрах в секунду).

Рис. 12.4. Флот электронов (маленькие точки), движущийся в едином направлении. Все электроны в трубке такого размера будут ежесекундно ударяться о зеркало

Мы знаем это, потому что все электроны, удаленные от зеркала на расстояние v × 1 с, будут ежесекундно врезаться в зеркало. Это относится ко всем электронам в трубке, изображенной на рисунке. Поскольку объем цилиндра равен площади его поперечного сечения, помноженной на длину, то объем трубки равен v м³, а поскольку во флоте электронов на 1 м³ приходится n электронов, значит, ежесекундно в зеркало врезается nv электронов.

Когда каждый электрон отскакивает от зеркала, он получает обратный импульс, то есть каждый электрон изменяет свой импульс на величину 2 mv. Сила требуется как для того, чтобы остановить движущийся автобус и отправить его в противоположном направлении, так и для поворота импульса электрона. И тут вновь в игру вступает Исаак Ньютон. В главе 1 мы записали его второй закон в виде F = ma, но вообще‑ то это частный случай более общего правила, которое гласит, что сила равна изменению импульса[59]. Итак, все электроны прикладывают к зеркалу общую силу F = 2 mv × (nv), потому что именно таково общее ежесекундное изменение импульса электронов. Благодаря тому, что пучок электронов имеет площадь 1 м², таково же будет и давление, оказываемое всеми электронами на зеркало.

От пучка электронов до газа, состоящего из электронов, лишь маленький шаг. Мы должны теперь учесть, что не все электроны движутся в одном направлении: какие‑ то движутся вверх, какие‑ то вниз, какие‑ то направо, какие‑ то налево и т. д. В результате мы должны разделить давление, оказываемое в любом направлении, на 6 (вспомните о шести гранях куба). Получится ( 2 mv) × (nv) / 6 = nmv ² / 3. В этом уравнении v можно заменить типичными скоростями движения электронов, которые мы получили в предыдущем уравнении (2) благодаря принципу неопределенности Гейзенберга, и вычислить общую величину давления, которое оказывают электроны в звезде – белом карлике[60]:

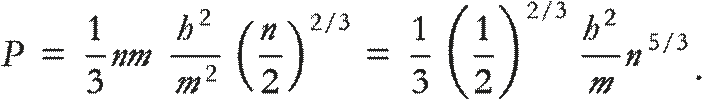
Если помните, мы предупреждали, что это приблизительный результат. Полный результат, для которого требуется гораздо больше математики, таков:

Это отличный результат. Он говорит, что давление в некотором месте звезды варьируется пропорционально количеству электронов на единицу объема в этом месте, возведенном в степень 5/3. Не беспокойтесь о том, что мы не получили константу пропорциональности в этих приблизительных расчетах, – важно, что все сошлось. Мы тем самым сказали также, что наша оценка импульса электронов, вероятно, чуть завышена, что объясняет, почему наша оценка давления оказалась выше истинного значения.

Выражение давления через плотность электронов – хорошее начало, но нашим целям лучше соответствовало бы выразить его через истинную плотность звезды. Это можно сделать, высказав на редкость безопасное предположение, что подавляющее большинство массы звезды приходится на ядра, а не на электроны (масса протона примерно в 2000 раз больше массы электрона). Мы знаем также, что количество электронов в звезде должно равняться количеству протонов, потому что звезда электрически нейтральна. Чтобы получить массовую плотность, мы должны знать, сколько протонов и нейтронов приходится на 1 м³ звезды, при этом о нейтронах забывать нельзя, так как это побочный продукт процесса синтеза. У более легких белых карликов ядро в основном будет состоять из гелия‑ 4, конечного продукта водородного синтеза, а следовательно, количество нейтронов и протонов будет одинаковым. Теперь немного об условных обозначениях. Номер атомной массы А условно используется для обозначения числа протонов и нейтронов в ядре. Для гелия‑ 4 А = 4.

Количество протонов в ядре мы обозначим буквой Z, для гелия Z = 2. Теперь можем выразить отношение между плотностью электронов n и массовой плотностью ρ:

n = Zρ / (mpA),

и мы предположили, что масса протона, mp, равна массе нейтрона, что вполне достаточно для наших целей.

Величина mpA – это масса каждого ядра; тогда ρ / mpA – количество ядер на единицу объема, а Z – количество протонов на единицу объема, которое должно совпадать с количеством электронов, что и получается в уравнении.

Мы можем воспользоваться этим уравнением, чтобы заменить n в уравнении (3), и поскольку n пропорционально ρ, то оказывается, что давление варьируется пропорционально плотности в степени 5/3. Мы только что обнаружили существенную физическую закономерность:

P = κ ρ 5/3, (4)

и не стоит слишком беспокоиться по поводу конкретных цифр, задающих общий масштаб давления, так что мы просто объединили их всех в символе κ. Стоит отметить, что κ зависит от отношения Z и А, а потому будет отличаться для разных видов звезд – белых карликов. Объединение чисел в одном символе позволяет увидеть, что здесь важно. В нашем случае символы могут отвлечь от самого существенного, а именно от зависимости между давлением и плотностью звезды.

Прежде чем мы продолжим, нужно отметить, что давление, оказываемое квантовыми колебаниями, не зависит от температуры звезды. Важна только степень ее сжатия. Давление электронов будет несколько большим, потому что электроны «нормальным образом» перемещаются благодаря своей температуре, и чем жарче звезда, тем интенсивнее они перемещаются. Об этом источнике давления мы не стали говорить, потому что мало времени, а если бы пришлось его рассчитывать, мы бы выяснили, что он ничтожен по сравнению с гораздо большим квантовым давлением.

Итак, мы наконец‑ то можем вставить уравнение квантового давления в ключевое уравнение (1), которое стоит здесь повторить:

Однако все не так просто, как кажется, потому что нужно знать еще разницу давлений на верхнюю и нижнюю грани куба. Можно полностью переписать уравнение (1) относительно плотности внутри звезды, которая сама по себе меняется от места к месту внутри звезды (иначе бы вокруг куба не существовало никакой разницы давлений), а потом попытаться решить его, чтобы определить, как плотность изменяется с расстоянием от центра звезды. Но при этом придется решать дифференциальное уравнение, а математики такого уровня мы хотим избежать. Проявим изобретательность и предпочтем подольше подумать и поменьше посчитать, чтобы применить уравнение (1) для вывода взаимосвязи между массой и радиусом звезды – белого карлика.

Очевидно, что размер нашего кубика и его расположение внутри звезды совершенно произвольны, поэтому никакие выводы о самой звезде не могут зависеть от этих деталей. Начнем с того, что сделаем нечто совершенно бесполезное на первый взгляд.

Мы имеем возможность выразить размер и местонахождение нашего куба через размер всей звезды. Если R – радиус звезды, можно записать расстояние куба от центра звезды как r = aR, где a – просто безразмерное число между 0 и 1. Под безразмерностью мы понимаем то, что оно не соответствует никакой единице, это только численный показатель. Если a = 1, то куб находится на поверхности звезды, а если a = ½, куб расположен строго посередине. Точно так же можно выразить размер куба через радиус звезды. Если L – длина стороны куба, мы можем записать L = bR, где b – это опять же только численный показатель, который должен быть очень мал, если наш куб мал относительно звезды. Здесь нет абсолютно ничего сложного, так что на этом этапе все должно казаться настолько простым, что записывать, кажется, даже бесполезно.

Заметим только, что использовать расстояние R совершенно естественно, потому что нет других относящихся к белому карлику расстояний, которые могли бы представлять сколь‑ нибудь разумную альтернативу.

Мы можем продолжать свои «бессмысленные» занятия и выразить плотность звезды в месте нахождения куба через среднюю плотность звезды. Запишем, что ρ = fρ ̅, где f – опять же просто численный показатель, а ρ ̅ – средняя плотность звезды. Как мы уже указывали, плотность куба зависит от его положения внутри звезды – чем ближе к центру, тем больше плотность. Так как средняя плотность ρ ̅ от положения куба не зависит, зависимость должен обнаруживать показатель f, который, таким образом, зависит от расстояния r, а следовательно, и от произведения aR. И это ключевая информация, лежащая в основе всех наших последующих вычислений: f – это чистое число, а R – не чистое число, а результат измерения расстояния. И f может зависеть только от a, а никак не от R. Это очень важный результат, потому что он свидетельствует, что плотность белого карлика «не зависит от масштаба». Это значит, что плотность изменяется на радиусе независимо от величины этого радиуса. Например, плотность в точке, расположенной на ¾ расстояния от центра до поверхности звезды, будет совершенно одинаковой в любом белом карлике независимо от его размера. Есть два способа оценки этого исключительно важного результата, и мы решили, что приведем здесь оба. Один из нас объясняет это так: «Дело в том, что любая безразмерная функция от r (а f – это именно она) может быть только безразмерной, так как это функция безразмерной переменной, а единственная безразмерная переменная в нашем случае – это r / R = a, поскольку R – единственная величина, связанная с расстоянием, из находящихся в нашем распоряжении».

Второй соавтор считает более четким следующее разъяснение: «f может в принципе по‑ разному сложным образом зависеть от r – расстояния кубика от центра звезды. Но давайте представим, что эти величины прямо пропорциональны, то есть f ∝ r. Иными словами, f = Br, где B – константа. Здесь самое важное то, что f – чисто численный показатель, в то время как r измеряется, например, в метрах. Отсюда следует, что B должно измеряться в 1/м, чтобы единицы расстояния взаимно сокращались. Итак, что нужно выбрать для B? Мы не можем назначить нечто произвольное, например «1 обратный метр», поскольку это бессмысленно и никак не связано со звездой. Почему, например, не выбрать один обратный световой год, получив совершенно другой ответ? Единственное расстояние, с которым мы имеем дело, – это R, физический радиус звезды, так что придется использовать его, чтобы f всегда оставалось чистым числом. Это значит, что f может зависеть только от r / R. Вы, наверное, уже поняли, что тот же вывод можно было сделать, если бы мы начали с предположения, что, например, f ∝ r ²». Собственно, ровно то же говорил и первый соавтор, только сейчас вышло длиннее.

Это значит, что можно выразить массу нашего кубика размером L и объемом L ³, находящегося на расстоянии r от центра звезды, в виде Mcube = f(a)L ³ ρ ̅. Мы написали f(a), а не просто f, чтобы не забывать, что f на деле зависит от нашего выбора a = r / R, а не от каких‑ то масштабных свойств звезды. Тот же аргумент можно использовать при указании, что мы можем записать Min = g(a)M, где g(a) – это опять же только функция от a. Например, функция g(a), высчитанная для a = ½, подсказывает, какое количество массы звезды приходится на сферу с радиусом, равным половине радиуса всей звезды, и это количество неизменно для всех белых карликов независимо от их радиуса по причине, приведенной в предыдущем абзаце[61]. Вы могли заметить, что мы постоянно избавляемся от тех символов, которые встречаются в уравнении (1), заменяя их безразмерными величинами (a, b, f и g), помноженными на величины, зависящие только от массы и радиуса звезды (средняя плотность звезды определяется через M и R, поскольку ρ ̅ = M / V и V = 4 π R ³ / 3, объем сферы). В довершение нужно сделать то же самое для разницы давлений, которую мы благодаря уравнению (4) можем записать как Pbottom – Ptop = = h(a, b)κ ρ ̅ 5/3, где h(a, b) – безразмерная величина. То, что h(a, b) зависит одновременно от a и b, связано с тем, что разница давлений зависит не только от местоположения куба (представленного a), но и от его объема (представленного b): у более крупных кубов больше разница давлений. Самое важное здесь то, что, как и f(a), и g(a), h(a, b) не может зависеть от радиуса звезды.

Мы можем воспользоваться только что выведенными выражениями и переписать уравнение (1):

Кажется, что в уравнении царит хаос; непохоже, чтобы уже на следующей странице мы пришли к результату. Главное – заметить, что уравнение выражает отношения между массой звезды и ее радиусом – конкретная зависимость между ними уже нащупывается (или на виду, но чудовищно далека – в зависимости от вашего уровня владения математикой). После введения в наше хаотическое уравнение средней плотности звезды (то есть ρ ̅ = M / (4π R ³ / 3)) оно принимает следующий вид:

где

Теперь λ зависит только от безразмерных величин a, b, f, g и h, а следовательно, не зависит от величин, которые описывают звезду в целом, M и R, а следовательно, λ должна иметь одно и то же значение для всех белых карликов.

Если вас интересует, что произойдет, если изменить a и/или b (то есть изменить местоположение и/или размеры нашего кубика), то вы упустили главное в наших аргументах. Если понимать буквально, кажется, что изменение a и b изменит и λ, так что мы получим другой результат для RM ⅓. Но ведь это невозможно, так как известно, что RM ⅓ зависит от самой звезды, а не от конкретных свойств того кубика, который мы придумали (или не придумали).

Это значит, что любые изменения a или b должны компенсироваться соответствующими изменениями f, g и h.

Уравнение (5) довольно уверенно утверждает, что белые карлики могут существовать. Дело в том, что нам удалось уравновесить уравнение гравитации‑ давления – уравнение (1). Это было не так‑ то просто: вполне могло оказаться, что уравнению не удовлетворяет ни одно сочетание M и R. Уравнение (5) также предсказывает, что величина RM ⅓ должна быть постоянной. Иными словами, если посмотреть на небо и измерить радиус и массу белых карликов, мы должны обнаружить, что радиус, помноженный на квадратный корень массы, даст один и тот же результат для любого белого карлика. Это смелое предсказание.

Только что изложенный аргумент можно еще усилить, поскольку возможно с точностью вычислить значение λ, правда, для этого придется решить дифференциальное уравнение второго порядка с учетом плотности, а такая математика лежит далеко за пределами нашей книги. Помните, что λ – это чистое число: оно значит только «то, что значит», и мы можем вычислить его с привлечением математики чуть более высокого уровня. Тот факт, что здесь мы не стали этим заниматься, не должен затмевать наших достижений: мы доказали, что белые карлики могут существовать, и сумели сделать предсказание, связанное с их массой и радиусом. После вычисления λ (которое можно выполнить на домашнем компьютере) и введения значений для κ и G наше предсказание примет вид:

RM ⅓ = (3, 5 × 1017 кг⅓ м) × (Z / A)5/3,

что равняется 1, 1 × 1017 кг1/3 м для ядер, состоящих из чистого гелия, углерода или кислорода (где Z / A = ½). Для железных ядер Z / A = 26/56, так что 1, 1 сводится почти к 1, 0. Мы пролистали справочную литературу и собрали данные о массах и радиусах 16 белых карликов, расположенных в Млечном Пути, ближайшей к нам галактике. Для каждой такой звезды мы вычислили значение RM ⅓, и результаты астрономических наблюдений показали, что оно приблизительно равно 0, 9 × 1017 кг⅓ м. Соответствие между наблюдениями и теоретическими выкладками просто поразительное: с помощью принципа Паули, принципа неопределенности Гейзенберга и закона притяжения Ньютона мы сумели предсказать зависимость между массой и радиусом для белых карликов.

Разумеется, в числах есть некая приблизительность (например, теория дает 1, 1 или 1, 0, а результат наблюдений – 0, 9). Будь у нас настоящий научный анализ, мы бы начали сейчас говорить, насколько вероятно полное соответствие теории эксперименту, но для наших целей такой аналитический уровень не столь необходим, потому что соответствие и так удивительно неплохое. Просто фантастика, что мы сумели подсчитать все это с погрешностью примерно 10 %, и это убедительное доказательство нашего приличного понимания квантовой механики и звезд.

Профессиональные физики и астрономы на этом бы не остановились. Они бы решили проверить теоретическое понимание в мельчайших подробностях, для чего следовало бы улучшить наше описание в эпилоге. В частности, уточненный анализ принял бы во внимание, что температура звезды все же играет некоторую роль в ее структуре. Более того, электроны роятся вокруг положительно заряженных атомных ядер, а в наших расчетах мы полностью пренебрегли взаимодействиями между электронами и ядрами (а заодно и между самими электронами). Мы не стали их учитывать, потому что сразу же заявили: они внесут лишь незначительные коррективы в простое решение. Это заявление было подтверждено более подробными расчетами, и вот почему наше упрощенное решение так хорошо соотносится с данными.

Очевидно, что мы узнали уже очень много нового: установили, что давление электронов способно поддерживать существование белого карлика, и сумели с определенной точностью предсказать, как меняется радиус звезды с прибавлением или снижением ее массы. Заметьте, что, в отличие от «обычных» звезд, интенсивно жгущих горючее, белые карлики парадоксальным образом уменьшаются с прибавлением массы. Это потому, что добавленная масса идет на увеличение гравитации звезды, заставляя ее сжиматься. На первый взгляд отношения, выраженные в уравнении (5), предполагают, что необходимо добавить бесконечное количество массы, прежде чем звезда сожмется до нулевого размера. Однако этого не происходит. Важно, как мы говорили в самом начале эпилога, что мы постепенно переходим в то состояние, когда электроны размещаются очень плотно, и первостепенную важность обретает специальная теория относительности Эйнштейна, потому что скорость электронов приближается к скорости света. В результате мы должны отказаться в расчетах от законов движения Ньютона, заменив их законами Эйнштейна. В этом‑ то все и дело.

Мы сейчас обнаружим, что при росте массивности звезды давление, оказываемое электронами, перестает быть пропорциональным плотности, возведенной в степень 5/3; с какого‑ то момента давление начинает возрастать медленнее, чем плотность. Расчеты мы проведем, но пока можно отметить, что это грозит катастрофическими последствиями для звезды. Дело в том, что при прибавлении массы обычное увеличение гравитации будет сопровождаться меньшим увеличением давления. Судьба звезды зависит от того, насколько меньшим будет это увеличение давления по сравнению с увеличением плотности, если электроны движутся быстро. Итак, настало время выяснить, каким будет давление «релятивистского» газа.

К счастью, нам не нужно выкатывать на сцену громоздкие механизмы теории Эйнштейна, потому что расчет давления в газе, который состоит из электронов, движущихся со скоростью, близкой к световой, производится почти по тем же лекалам, что и для газа, состоящего из «медленных» электронов. Ключевая разница в том, что мы не можем более опираться на уравнение p = mv, так как это становится некорректным. Однако по‑ прежнему верно, что сила, с которой действуют электроны, равна изменению их импульса. Ранее мы вывели, что флот электронов, отражающихся от зеркала, оказывает давление P = 2 mv × (nv). Для релятивистского случая можно записать то же выражение, заменив mv импульсом p. Мы также полагаем, что скорость электронов близка к скорости света, так что заменяем v на c. Наконец, чтобы получить давление в звезде, нужно не забывать о делении на 6. Итак, мы можем записать давление для релятивистского газа как P = 2 p × nc / 6 = pnc / 3.

Как и ранее, можем воспользоваться принципом неопределенности Гейзенберга и указать, что, поскольку типичный импульс ограниченных электронов равен h(n/2) ⅓, то

Мы опять можем сравнить этот результат с точным решением, которое выглядит так:

Наконец, можем воспользоваться привычной методологией, чтобы выразить давление через массовую плотность звезды и вывести альтернативу уравнению (4):

P = κ ' ρ 4/3,

где κ ' ∝ hc × (Z / (Amp)) 4/3. Как мы и обещали, давление, аналогично плотности, увеличивается медленнее, чем в нерелятивистском случае, а именно: плотность увеличивается со степенью 4/3, а не 5/3. Причина такого замедления кроется в том, что электроны не могут двигаться быстрее скорости света. Это значит, что «векторный» показатель nv, который мы использовали для вычисления давления, перенасыщается в nc, и газ не может перенести электроны к зеркалу (или грани куба), чтобы поддерживалась плотность ρ 5/3. Теперь можно изучить последствия таких изменений, поскольку с помощью тех же рассуждений, что и в нерелятивистском случае, мы можем прийти к аналогу уравнения (5):