Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вычисление ранга матрицы.
|
|
Рассмотрим матрицу типа [n´ m]:
Если в этой матрице выделить произвольно k столбцов и k строк, то элементы, стоящие на пересечении выделенных столбцов и строк, образуют квадратную матрицу k -го порядка. Определитель этой матрицы называется минором k -го порядка матрицы А. Очевидно, что матрица А обладает минорами любого порядка от 1 до наименьшего из чисел m и n. Среди всех отличных от нуля миноров матрицы А найдётся, по крайней мере, один минор, порядок которого будет наибольшим.
Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы.
Если все элементы матрицы А равны нулю, то говорят, что ранг матрицы А равен нулю. Если ранг матрицы А равен r, то это означает, что в матрице А имеется, по крайней мере, один, отличный от нуля минор порядка r, но всякий минор порядка, большего чем r, равен нулю. Ранг матрицы А обозначается через r(А).
Очевидно, что всегда выполняется соотношение
0 £ r £ min (m, n).
Свойство 1. При транспонировании матрицы её ранг не меняется.
Свойство 2. Ранг матрицы не меняется при перестановке её столбцов (строк).
Свойство 3. Ранг матрицы не меняется при умножении всех элементов её столбца (строки) на отличное от нуля число.
Свойство 4. Ранг матрицы не изменится, если к одному из её столбцов (строк) прибавить другой столбец (строку), умножив его (её) на некоторое число.
Свойство 5. Ранг матрицы не изменится, если удалить из неё столбец (строку), состоящий из одних нулей.
Свойство 6. Ранг матрицы не изменится, если удалить из неё столбец (строку), являющийся линейной комбинацией других столбцов (строк).
Элементарными называются следующие преобразования матриц:
перестановка двух любых столбцов (строк);
умножение столбца (строки) на отличное от нуля число;
прибавление к одному столбцу (строке) линейной комбинации других столбцов (строк).
Из перечисленных выше свойств ранга матрицы следует, что при элементарных преобразованиях матрицы её ранг не меняется.
Две матрицы называют эквивалентными, если одна из них получается из другой с помощью применения конечного множества элементарных преобразований. Эквивалентные матрицы не являются равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: А~В.
Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы равны нулю, например:
При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической.
Ранг канонической матрицы равен числу единиц на её главной диагонали.
На практике для вычисления ранга матрицы достаточно привести матрицу к ступенчатому виду.
Пусть нам дана матрица А, имеющая следующий вид:
Чтобы вычислить ранг матрицы А, необходимо с помощью элементарных преобразований, преобразовать её к такому виду, в котором все элементы, располагающиеся ниже главной диагонали, были равны нулю. Для этого произведём анализ строк матрицы А. Интерес вызывает 2-я строка, в которой 1-й элементы равен 1, следовательно, используя свойства 1-4, во всех строках, кроме этой, получить ряд нулевых элементов с помощью следующих преобразований над строками:
к элементам 1-ой строки прибавим элементы 2-ой, умноженные на (-2);
к элементам 3-ей строки прибавим элементы 2-ой, умноженные на (-2);
к элементам 4-ой строки прибавим элементы 2-ой, умноженные на (-3).
В результате получим матрицу Ā ~А:
где вторая строка матрицы А становится первой строкой в матрице Ā.
25)
a11x1+a12x2+…+a1nxn=b1, где a1n называются коэффициентами при неизвестных, а b- свободным коэффициентом. Два линейных ур-я называются равносильными, если есть общее решения. Система уравнений называется совместной, если она имеет хотя бы одно решение. Система ур-ий называется определённой, если она имеет одно единственное решение, и неопределённой, если решений множество. Матрица, эл-тами которой являются коэффициенты при неизвестных системы, называется матрицей системы. Матрица системы, дополненная столбцом свободных коэффициентов, называется расширенной матрицей.
- матричная запись системы.
Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы. RgA = RgA*.Очевидно, что система (1) может быть записана в виде: x1 
+ x2 
+ … + xn 
Доказательство. 1) Если решение существует, то столбец свободных членов есть линейная комбинация толбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А®А* не изменяют ранга.2) Если RgA = RgA*, то это означает, что они имеют один и тот же Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше Пример. Определить совместность системы линейных уравнений:
A = 
~ 
. 
RgA = 2.A* = 
RgA* = 3.Система несовместна. Пример. Определить совместность системы линейных уравнений. 
А = 
; 
= 2 +
+12 = 14 ¹ 0; RgA = 2; A* = 
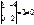RgA* = 2.Система совместна. Решения: x1 = 1; x2 =1/2.
Теорема 4.2 (теорема Кронекера-Капелли). Система (2.2) совместна тогда и только тогда, если ранг матрицы системы равен рангу расширенной матрицы.
Доказательство.
1) Необходимость: пусть система (2.2) совместна и ее решение. Тогда
, (4.1) то есть столбец свободных членов является линейной комбинацией столбцов матрицы системы и, следовательно, столбцов любого ее базисного минора. Поэтому добавление элементов этого столбца и любой строки расширенной матрицы к базисному минору даст нулевой определитель, то есть
2) Достаточность: если то любой базисный минор матрицы А является и базисным минором расширенной матрицы. Поэтому столбец свободных членов представляет собой линейную комбинацию столбцов этого базисного минора, и, следовательно, линейную комбинацию всех столбцов матрицы А. Если обозначить коэффициенты этой линейной комбинации то эти числа будут решением системы (2.2), т.е. эта система совместна. Теорема доказана.
26)
Линейное пространство в линейной алгебре, да и не только в линейной алгебре, определяется следующим образом:
Множество А называется линейным векторным аффинным пространством, если
· Каждым двум элементам множества А соответствует некоторый третий элемент, называемый их суммой и принадлежащий множеству А.
· Для каждого элемента множества А и каждого числа из заданного числового множества существует элемент множества А, называемый произведением вектора на число.
Эти операции удовлетворяют следующим условиям:
· x+y=y+x коммутативность
· (x+y)+z=x+(y+z) ассоциативность
· существует элемент 0 такой, что x+0=x
· для каждого x существует элемент -x, такой что x+(-x)=0
· 1*x=x
· a*(b*x)=(a*b)*x
· (a+b)x=ax+bx
· a(x+y)=ax+ay
Центральным понятием в линейной алгебре является понятие размерности линейного пространства, для которого используется определение линейной независимости векторов.
Система векторов линейного пространства называется линейно независимой если любая ее линейная комбинация, равная нулю имеет все коэффициенты нулевые.
Если найдется хотя бы одна линейная комбинация с отличными от нуля коэффициентами, равная нулю, то система векторов линейного пространства линейно зависима.
Существуют линейные пространства, имеющие линейно независимые системы векторов, состоящие из сколь угодно большого числа элементов. Такие пространства называются бесконечномерными.
Наоборот существуют пространства, в которых нет линейно независимых систем векторов, состоящих из сколь угодно большого числа элементов. Такие пространства называются конечномерными.
Можно показать, что в конечномерных пространствах все системы векторов состоящие из n+1 элементов и более линейно зависимы, но тем не менее существуют линейно независимые системы векторов, состоящие из n элементов. В таком случае число n называется размерностью линейного пространства.
Любая совокупность векторов, состоящая из n элементов векторного пространства называется базисом пространства.
|
|