
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Умножение матрицы на число.
|
|
Умножение матрицы A на число λ заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен: bij = λ aij.
Сложение матриц
Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен: cij = aij + bij.
Умножение матриц.
Умножение матриц (обозначение: AB, реже со знаком умножения AxB) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго:
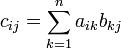
Количество столбцов в матрице A должно совпадать с количеством строк в матрице B. Если матрица A имеет размерность mxn, B — nxk, то размерность их произведения AB = C есть mxk.
Транспонирование.
Транспонированную матрицу можно получить, поменяв строки и столбцы матрицы местами. A = (aij), то AT = (aji).
Симметричной матрицей называют квадратную матрицу, элементы которой симметричны относительно главной диагонали. Это означает, что она равна её транспонированной матрице.
Ранг матрицы
Количество линейно независимых строк матрицы называют строчным рангом матрицы, а количество линейно независимых столбцов матрицы называют столбцовым рангом матрицы. В действительности, оба ранга совпадают. Их общее значение и называется рангом матрицы.
Другой эквивалентный данному подход заключается в определении ранга матрицы, как максимального порядка отличного от нуля минора матрицы.
ОБРАТНАЯ МАТРИЦА
Обра́ тная ма́ трица — такая матрица A-1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:
A*A-1 = A-1*A = E.
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.

Обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицу алгебраических дополнений элементов исходной матрицы.
C* - матрица, составленная из алгебраических дополнений для соответствующих элементов транспонированной матрицы.
МАТРИЧНЫЕ ОПЕРАЦИИ:
Сложение и вычитание допускается только для матриц одинакового размера.
Существует нулевая матрица такая, что её прибавление к другой матрице A не изменяет A, то есть: A + 0 = A
Все элементы нулевой матрицы равны нулю.
Возводить в степень можно только квадратные матрицы.
Ассоциативность сложения: A + (B + C) = (A + B) + C.
Коммутативность сложения: A + B = B + A.
Ассоциативность умножения: A(BC) = (AB)C.
Дистрибутивность умножения относительно сложения:
A(B + C) = AB + AC.
(B + C)A = BA + CA.
Свойства операции транспонирования матриц:
(AT)T = A
(AB)T = BTAT
(A − 1)T = (AT) − 1, если обратная матрица A - 1 существует.
(A + B)T = AT + BT
detA = detAT .
Элементарными преобразованиями матрицы называются преобразования следующих трёх типов:
Перестановка двух строк или столбцов матрицы;
Умножение строки или столбца на число отличное от нуля;
Прибавление к одной строке или столбцу матрицы другой её строки или столбца, умноженной на любое число!
Минором элемента матрицы называется определитель матрицы, полученной вычеркиванием строки и столбца, в которых расположен элемент. Обозначаем: минор элемента
aij =  .
.
Следствие: Определитель треугольной матрицы равен произведению диагональных элементов.
СВОЙСТВА ОПРЕДЕЛИТЕЛЯ:
Свойство 1. При замене строк столбцами (транспонировании) значение определителя не изменится, т.е.
 .
.
Свойство 2. Если хотя бы один ряд (строка или столбец) состоит из нулей, то определитель равен нулю.
Свойство 3. Если в определителе поменять местами два соседних параллельных ряда (строки или столбцы), то определитель поменяет знак на противоположный, т.е.
 .
.
Свойство 4. Если в определителе имеются два одинаковых параллельных ряда, то определитель равен нулю:

Свойство 5. Если в определителе два параллельных ряда пропорциональны, то определитель равен нулю:

Свойство 6. Если все элементы определителя, стоящие в одном ряду, умножить на одно и то же число, то значение определителя изменится в это число раз:
 .
.
Следствие. Общий множитель, содержащийся во всех элементах одного ряда, можно вынести за знак определителя, например:
 .
.
Свойство 7. Если в определителе все элементы одного ряда представлены в виде суммы двух слагаемых, то он равен сумме двух определителей:
 .
.
Свойство 8. Если к элементам какого-либо ряда прибавить произведение соответствующих элементов параллельного ряда на постоянный множитель, то значение определителя не изменится:
 .
.
Свойство 9. Если к элементам i-го ряда прибавить линейную комбинацию соответствующих элементов нескольких параллельных рядов, то значение определителя не изменится:
 .
.
Следствие. Определитель единичной матрицы равен единице  .
.
Система m линейных уравнений с n неизвестными в линейной алгебре — это система уравнений вида:

Здесь x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.
Система называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Система называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему обращает все её уравнения в тождества.
Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
Совместная система вида может иметь одно или более решений.
Система линейных уравнений может быть представлена в матричной форме как:
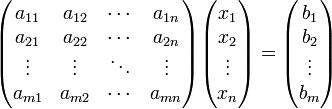
Если к матрице А приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.
15)
Определи́ тель (или детермина́ нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.
Определитель матрицы А обозначается как: det(A), |А| или Δ (A).
Определение через разложение по первой строке

Схема расчета определителя матрицы  .
.
Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:

Для матрицы  детерминант определяется как
детерминант определяется как

Для матрицы  определитель задаётся рекурсивно:
определитель задаётся рекурсивно:
 , где
, где  — дополнительный минор к элементу a 1 j . Эта формула называется разложением по строке.
— дополнительный минор к элементу a 1 j . Эта формула называется разложением по строке.
В частности, формула вычисления определителя матрицы  такова:
такова:

= a 11 a 22 a 33 − a 11 a 23 a 32 − a 12 a 21 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 − a 13 a 22 a 31
Легко доказать, что при транспонировании определитель матрицы не изменяется (иными словами, аналогичное разложение по первому столбцу также справедливо, то есть даёт такой же результат, как и разложение по первой строке):

Определение через перестановки
Для матрицы  справедлива формула:
справедлива формула:
 ,
,
где α 1, α 2,..., α n — перестановка чисел от 1 до n, N (α 1, α 2,..., α n) — число инверсий в перестановке, суммирование идёт по всем возможным перестановкам порядка n. Таким образом, в определитель войдёт n! слагаемых, которые также называют «членами определителя». Важно заметить, что во многих курсах линейной алгебры это определение даётся как основное.
Свойства определителей
§ Определитель — кососимметричная полилинейная функция строк (столбцов) матрицы. Полилинейность означает, что определитель линеен по всем строкам (столбцам):  , где
, где  и т. д. — строчки матрицы,
и т. д. — строчки матрицы, 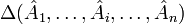 — определитель такой матрицы.
— определитель такой матрицы.
§ При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.
§ Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.
§ Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.
§ Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).
§ Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
§ Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.
§ Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.
§ Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
§ Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей (cм. также формулу Бине-Коши).
§ С использованием индексной нотации определитель матрицы 3× 3 может быть определён с помощью символа Леви-Чивита из соотношения:

16)
Теорема Лапласа
Определение. Выделим в det A строки с номерами α 1 <... < α k и столбцы
с номерами β 1 <... < β k. Элементы aα jβ ℓ, стоящие в этих строках и
столбцах, образуют определитель k -го порядка:
M = A _ α 1 ... α k
β 1 ... β k _ def =______
aα 1 β 1 ... aα 1 β k
......
aα kβ 1 ... aα kβ k
______
Он называется минором k -го порядка определителя det A. Если же из
определителя det A вычеркиваются строки и столбцы с указанными номе-
рами, то получившийся определитель (n − k)-го порядка
A _ α k +1 ... α n
β k +1 ... β n _ здесь {α k +1 <... < α n} ⊂ { 1, 2 ,..., n} \ {α 1 ,... α k}
{β k +1 <... < β n} ⊂ { 1, 2 ,..., n} \ {β 1 ,... β k}
называется минором, дополнительным минору M в det A. Число
_ M def = (− 1) α 1+ ... + α k + β 1+ ... + β kA _ α k +1 ... α n
β k +1 ... β n _
называется алгебраическим дополнением минора M в det A.
Теорема 7.1 (Лаплас). Выделим в det A произвольные строки с номерами
α 1 <... < α k. Образуем всевозможные миноры k-го порядка с элементами
из этих строк:
A _ α 1 ... α k
β 1 ... β k _, здесь {β 1 <... < β k} ⊂ { 1, 2 ,..., n}.
Домножим эти миноры на их алгебраические дополнения в det A. Тогда ве-
личина det A равна сумме таких произведений по всем возможным выборкам
k элементов (β 1 ,..., β k) из { 1, 2 ,..., n}:
det A =
= _ 1 ≤ β 1 <...< β k≤ n
A _ α 1 ... α k
β 1 ... β k _ A _ α k +1 ... α n
β k +1 ... β n _(− 1)_ α 1+ ... + α k +
+ β 1+ ... + β k _.
|
|