
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение экстремума функции методом скорейшего спуска
|
|
Теоретические положения
Рассмотренные в предыдущих лабораторных работах задачи относятся к задачам линейного программирования. Однако в реальных экономических моделях такие показатели, как прибыль, себестоимость, капитальные затраты на производство и др., в действительности нелинейно зависят от объема производства, расхода ресурсов и т.п. В этом случае возникает задача нелинейного программирования.
Допустим, что среди ограничений нет неравенств, не обязательны условия неотрицательности, переменные не являются дискретными, m < n, а функции непрерывны и имеют частные производные по крайней мере второго порядка. В этом случае задачу оптимизации можно сформулировать так: найти переменные x  , x
, x  , …, x
, …, x 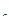 , удовлетворяющие системе уравнений
, удовлетворяющие системе уравнений
 (x
(x  , x
, x  , …, x
, …, x 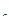 ) = b
) = b  , i = 1, 2, …, m
, i = 1, 2, …, m
и обращающие в максимум (минимум) целевую функцию
z = f(x  , x
, x  , …, x
, …, x 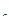 ).
).
Функция z может иметь произвольный нелинейный вид.
Для решения сформулированной задачи могут быть использованы классические методы оптимизации. Для этого следует четко представлять различие между локальным экстремумом функции, глобальным экстремумом и условным экстремумом.
Будем полагать, что функция z = f(x  , x
, x  , …, x
, …, x 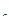 ) = f(X) дважды дифференцируема в точке X
) = f(X) дважды дифференцируема в точке X  = (x
= (x 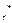 , x
, x  , …, x
, …, x  ) и некоторой ее окрестности. Если для всех точек Х этой окрестности f(X
) и некоторой ее окрестности. Если для всех точек Х этой окрестности f(X  )
)  f(X) или f(X
f(X) или f(X  )
)  f(X), то говорят, что функция f(X) имеет экстремум в X
f(X), то говорят, что функция f(X) имеет экстремум в X  (соответственно максимум или минимум). Точка X
(соответственно максимум или минимум). Точка X  , в которой все первые частные производные равны 0, называется стационарной точкой.
, в которой все первые частные производные равны 0, называется стационарной точкой.
Необходимое условие экстремума. Если в точке X  функция z = f(X) имеет экстремум, то первые частные производные функции в этой точке равны нулю:
функция z = f(X) имеет экстремум, то первые частные производные функции в этой точке равны нулю:
f  (X
(X  ) = 0, i = 1, 2, …, n.
) = 0, i = 1, 2, …, n.
Для получения достаточных условий следует определить в стационарной точке знак дифференциала второго порядка
d  f(X) =
f(X) =  (X)
(X)  x
x 
 x
x  .
.
Достаточные условия экстремума функции двух переменных. Найдем значения частных производных второго порядка в стационарной точке X 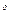 (x
(x  , x
, x  ):
):
a  =
=  (X
(X 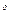 ); a
); a  =
=  (X
(X 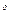 ); a
); a  =
=  (X
(X 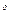 ); a
); a  =
=  (X
(X 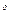 ).
).
Составим определитель из a  для i, j = 1, 2:
для i, j = 1, 2:
 = a
= a  a
a  – a
– a  a
a  .
.
Достаточные условия экстремума имеют вид:
a) если  > 0 и a
> 0 и a  < 0, то в точке X
< 0, то в точке X 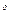 функция имеет максимум; если
функция имеет максимум; если  > 0 и a
> 0 и a  > 0, то в точке X
> 0, то в точке X 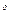 – минимум;
– минимум;
б) если  < 0, то минимума нет;
< 0, то минимума нет;
в) если  = 0, то вопрос об экстремуме остается открытым.
= 0, то вопрос об экстремуме остается открытым.
Приведенная схема позволяет определить локальный экстремум функции двух переменных.
Функция z = f(x  , x
, x  , …, x
, …, x 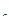 ) = f(X) имеет в точке (X
) = f(X) имеет в точке (X 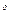 ) заданной области D глобальный максимум или глобальный минимум, если неравенство f(X)
) заданной области D глобальный максимум или глобальный минимум, если неравенство f(X)  f(X
f(X 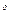 ) или f(X)
) или f(X)  f(X
f(X 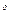 ) соответственно выполняется для любой точки X
) соответственно выполняется для любой точки X  D.
D.
Если область D замкнута и ограничена, то дифференцируемая функция z = f(X) достигает в этой области своих наибольшего и наименьшего значений или в стационарной точке, или в граничной точке области (теорема Вейерштрасса).
Условный экстремум. Пусть необходимо найти экстремум функции z = f(x  , x
, x  , …, x
, …, x 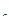 ) при условии, что переменные x
) при условии, что переменные x  , x
, x  , …, x
, …, x 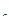 удовлетворяют уравнениям
удовлетворяют уравнениям
 (x
(x  , x
, x  , …, x
, …, x 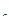 ) =0, i = 1, 2, …, m, m < n.
) =0, i = 1, 2, …, m, m < n.
Эти уравнения называются уравнениями связей.
Говорят, что в точке X 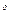 (x
(x  , x
, x  , …, x
, …, x  ), удовлетворяющей уравнениям связи, функция z = f(X) имеет условный максимум (минимум), если неравенство f(X
), удовлетворяющей уравнениям связи, функция z = f(X) имеет условный максимум (минимум), если неравенство f(X 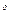 )
)  f(X) (f(X
f(X) (f(X 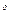 )
)  f(X)) имеет место для всех точек Х, координаты которых удовлетворяют уравнениям связи.
f(X)) имеет место для всех точек Х, координаты которых удовлетворяют уравнениям связи.
Градиентом  F функции F(X) = F(x
F функции F(X) = F(x  , x
, x  , …, x
, …, x 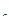 ) называется вектор, проекциями которого на координатные оси служат соответствующие частные производные, т.е.
) называется вектор, проекциями которого на координатные оси служат соответствующие частные производные, т.е.
 F =
F =  .
.
В каждой точке Х направление градиента является направлением наибольшего возрастания функции, а модуль градиента равен наибольшей скорости возрастания функции в этой точке.
Функция F(X) = F(x  , x
, x  , …, x
, …, x 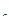 ), определенная на выпуклом множестве М n-мерного пространства, называется выпуклой на этом множестве, если
), определенная на выпуклом множестве М n-мерного пространства, называется выпуклой на этом множестве, если
F(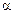 X
X  + (1 –
+ (1 – 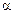 )X
)X  )
) 
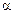 F(X
F(X  ) + (1 –
) + (1 – 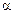 )F(X
)F(X  )
)
для любых точек X  , X
, X 
 М и любого числа
М и любого числа  .
.
Для определения выпуклости конкретной конкретной функции, часто используют критерий Сильвестра. Функция является выпуклой тогда и только тогда, когда неотрицательны все главные миноры 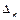 матрицы вторых частных производных, т.е. определители
матрицы вторых частных производных, т.е. определители
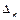 =
=  , a
, a  =
=  , k = 1, 2…, n.
, k = 1, 2…, n.
Задача выпуклого программирования состоит в отыскании такого решения системы ограничений, при котором выпуклая целевая функция достигает минимального значения, или вогнутая функция достигает максимального значения.
Решение задач выпуклого программирования методом скорейшего спуска.
Схема решения задач методами спуска состоит в построении последовательности
X  , X
, X  , …, X
, …, X  , …
, …
решений системы ограничений задачи по следующему принципу: в качестве X  выбирается произвольная точка области решений, а каждая последующая точка получается из предыдущей по формуле:
выбирается произвольная точка области решений, а каждая последующая точка получается из предыдущей по формуле:
X  = X
= X  +
+  l,
l,
где l = (l  , …, l
, …, l  ) – некоторое направление (т.е. вектор), а
) – некоторое направление (т.е. вектор), а  – число. При этом направление l и«длина шага»
– число. При этом направление l и«длина шага»  выбирается так, чтобы обеспечить сходимость последовательности к оптимальному решению Х
выбирается так, чтобы обеспечить сходимость последовательности к оптимальному решению Х  . Так как направление градиента
. Так как направление градиента  Z целевой функции является направлением ее наискорейшего роста, то при отыскании максимума вогнутой функции (минимума выпуклой) в качестве l берется
Z целевой функции является направлением ее наискорейшего роста, то при отыскании максимума вогнутой функции (минимума выпуклой) в качестве l берется  Z и формула принимает вид:
Z и формула принимает вид:
X  = X
= X  +
+  ∙
∙  Z(Х
Z(Х  ), если ищется Z
), если ищется Z  ,
,
X  = X
= X  –
–  ∙
∙  Z(Х
Z(Х  ), если ищется Z
), если ищется Z  .
.
Если величина  выбирается так, чтобы приращение функции
выбирается так, чтобы приращение функции  Z при перемещении из точки X
Z при перемещении из точки X  в точку X
в точку X  было наибольшим (при отыскании Z
было наибольшим (при отыскании Z  ) или наименьшим (при отыскании Z
) или наименьшим (при отыскании Z  ), то градиентный метод называется методом скорейшего спуска. Можно доказать, что требования скорейшего спуска выполняются при соблюдении условия:
), то градиентный метод называется методом скорейшего спуска. Можно доказать, что требования скорейшего спуска выполняются при соблюдении условия:
 Z(Х
Z(Х  )∙
)∙  Z(Х
Z(Х  ) = 0.
) = 0.
Произведение в этом выражении означает скалярное произведение векторов градиентов в соседних точках.
Пример
Найти методом скорейшего спуска с точностью до 0, 01 экстремум функции Z = 2x  – x
– x  x
x  + x
+ x 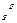 – x
– x  – x
– x  + 1 при ограничениях x
+ 1 при ограничениях x  + x
+ x 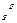
 4, x
4, x 
 0, x
0, x 
 0.
0.
|
|