Отдача от масштаба

Теперь рассмотрим эксперимент иного рода. Вместо того чтобы увеличивать количество одного применяемого фактора, сохраняя количество другого фактора неизменным, будем увеличивать количество всех факторов, от которых зависит производственная функция. Другими словами, умножим количество всех факторов на некий постоянный множитель: например, будем использовать в два раза больше как фактора 1, так и фактора 2.

Какой объем выпуска мы получим, если будем использовать в два раза больше каждого фактора? При наиболее вероятном исходе, мы получим вдвое больший объем выпуска. Этот случай называют случаем постоянной отдачи от масштаба. В терминах производственной функции это означает, что удвоение количества каждого фактора производства приносит удвоение объема выпуска. Математически для случая двух факторов это можно выразить в виде

2 f (x ₁, x ₂) = f (2 x ₁, 2 x ₂).

Вообще, если мы увеличиваем количество всех факторов в одно и то же число раз t, постоянная отдача от масштаба означает, что мы должны получить в t раз больший объем выпуска:

tf (x ₁, x ₂) = f (tx ₁, tx ₂).

Мы считаем этот исход вероятным по следующей причине: как правило, фирма должна быть способна повторить то, что она делала раньше. Если у фирмы имеется в два раза больше каждого фактора производства, то она может просто открыть рядом два завода и в результате получить вдвое больший выпуск. Имея в три раза больше каждого фактора, она может открыть три завода и т.д.

Обратите внимание на то, что технология вполне может характеризоваться постоянной отдачей от масштаба и при этом убыванием предельного продукта каждого фактора. Отдача от масштаба описывает то, что происходит при увеличении количества всех факторов, в то время как убывание предельного продукта описывает то, что происходит при увеличении количества одного из факторов и сохранении неизменным количества остальных факторов.

Постоянная отдача от масштаба в силу приведенного довода о повторении результата является наиболее " естественным" случаем, но вовсе не означает, что невозможны другие исходы. Например, могло бы случиться так, что при умножении количеств обоих факторов на какой-то множитель t мы получили бы более чем в t раз больший выпуск. Этот случай называют случаем возрастающей отдачи от масштаба. Математически возрастающая отдача от масштаба означает, что

f (tx ₁, tx ₂) > tf (x ₁, x ₂).

для всех t > 1.

Какая технология дает пример возрастающей отдачи от масштаба? Один из удачных примеров такого рода — технология производства нефтепровода. Удваивая диаметр трубы, мы используем вдвое больше материалов, но площадь поперечного сечения трубы увеличивается в четыре раза. Поэтому мы, скорее всего, сможем прокачать через нее более чем вдвое больше нефти.

(Разумеется, в этом примере нам не следует заходить слишком далеко. Если продолжать удваивать диаметр трубы, она в конце концов рухнет под тяжестью собственного веса. Возрастающая отдача от масштаба обычно наблюдается лишь в определенном диапазоне выпуска.)

Следует рассмотреть также случай убывающей отдачи от масштаба, при которой

f (tx ₁, tx ₂) < tf (x ₁, x ₂)

для всех t > 1.

Этот случай несколько специфичен. Если от удвоения количества каждого фактора мы получаем менее, чем вдвое больший выпуск, мы, должно быть, делаем что-то не так. В конце концов мы ведь могли бы просто повторить то, чтали раньше!

Убывающая отдача от масштаба обычно возникает из-за того, что мы забыли учесть какой-то фактор производства. Если у нас вдвое больше каждого фактора, за исключением одного, мы уже не сможем в точности повторить то, что делали раньше, так что нет причин ожидать, что мы получим выпуск, вдвое больший. Убывающая отдача от масштаба есть, на самом деле, явление, наблюдающееся в коротком периоде, когда количество какого-либо фактора сохраняется постоянным.

Разумеется, одна и та же технология может характеризоваться различной отдачей от масштаба при разных уровнях производства. Вполне может случиться, что при более низких объемах производства технология характеризуется возрастающей отдачей от масштаба — по мере умножения количеств факторов на какую-то малую величину t выпуск возрастает более чем в t раз. Позднее, для более высоких уровней выпуска, увеличение количеств факторов в t раз может привести к увеличению выпуска как раз в t раз.

Краткие выводы

1. Технологические ограничения фирмы описываются производственным множеством, которое показывает все технологически допустимые ком-бинации вводимых ресурсов (факторов производства) и выпусков, и производственной функцией, которая показывает максимальный объем выпуска, связанный с данным количеством факторов производства.

2. Другой способ описания технологических ограничений фирмы состоит в использовании изоквант — кривых, показывающих все комбинации факторов производства, с помощью которых можно произвести данный объем выпуска.

3. Обычно мы предполагаем, что изокванты выпуклы и монотонны, подобно кривым безразличия для стандартных предпочтений.

4. Предельный продукт измеряет добавочный объем выпуска, приходящийся на добавочную единицу фактора, при неизменности количеств всех остальных факторов. Как правило, мы предполагаем, что предельный продукт фактора, по мере увеличения использования данного фактора, убывает.

5. Технологическая норма замещения (TRS) измеряет наклон изокванты. Обычно мы предполагаем, что при движении вдоль изокванты TRS убы-вает — это лишь другой способ утверждать, что изокванта имеет выпук-лую форму.

6. В коротком периоде некоторые факторы производства постоянны, в то время как в длительном периоде все факторы производства переменны.

7. Отдача от масштаба характеризует то, как меняется объем выпуска с изменением масштаба производства. Если мы увеличиваем количества всех факторов в одно и то же число раз t и объем выпуска возрастает во столько же раз, то мы имеем дело с постоянной отдачей от масштаба. Если выпуск возрастает более чем в t раз, мы имеем дело с возрастающей отдачей от масштаба; если выпуск возрастает менее чем в t раз — перед нами убывающая отдача от масштаба.

Минимизация издержек. Изокосты. Производный спрос на факторы производства. Аксиома минимизации издержек. Функции издержек в коротком и долгом периодах. Квази-фиксированные издержки.19.1. Минимизация издержек

14. Предположим, что у нас имеется два фактора производства с ценами w ₁ и w ₂ и мы хотим найти самый дешевый способ производства заданного объема выпуска y. Если обозначить используемые количества каждого из двух факторов через x ₁ и x ₂, а производственную функцию для фирмы — через f (x ₁, x ₂), то эту задачу можно записать в видmin w ₁ x ₁ + w ₂ x ₂ x ₁, x ₂ при f (x ₁, x ₂) = y.

15. При проведении подобного рода анализа следует сделать те же предупреждения, что и в предыдущей главе: убедитесь, что вы включили в подсчет издержек все издержки производства и что все измерения производятся в совместимом временном масштабе.

Решение этой задачи минимизации издержек — величина минимальных издержек, необходимых для достижения определенного объема выпуска, — будет зависеть от w ₁, w ₂ и y, поэтому мы запишем это решение как c (w ₁, w ₂, y). Эта функция известна как функция издержек, и она будет представлять для нас значительный интерес. Функция издержек c (w ₁, w ₂, y) показывает минимальные издержки производства y единиц выпуска при ценах факторов, равных (w ₁, w ₂).

Чтобы понять решение этой задачи, изобразим функцию издержек и технологические ограничения для фирмы на одном графике. Изокванты дают нам технологические ограничения — все комбинации x ₁ и x ₂, с помощью которых можно произвести y.

Предположим, что мы хотим нанести на график все комбинации факторов, дающие один и тот же уровень издержек C. Мы можем записать это в виде выражения

w ₁ x ₁ + w ₂ x ₂ = C,

которое может быть преобразовано в

x ₂ = — x ₁.

Легко увидеть, что это уравнение прямой, имеющей наклон — w ₁/ w ₂ и точку пересечения с вертикальной осью C / w ₂. Изменяя число C, мы получаем целое семейство изокост. Каждая точка изокосты выражает одни и те же издержки C, и более высокие изокосты связаны с большими издержками.

Таким образом, наша задача минимизации издержек может быть перефразирована следующим образом: найти на изокванте точку, с которой связана самая низкая изокоста. Такая точка показана на рис.19.1.

Обратите внимание на то, что если оптимальное решение предполагает использование некоторого количества каждого из факторов и если изокванта представляет собой гладкую кривую, то точка минимизации издержек будет характеризоваться условием касания: наклон изокванты должен быть равен наклону изокосты. Или, пользуясь терминологией гл.17, технологическая норма замещения должна равняться отношению цен факторов:

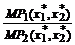— = TRS( 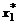, ) = — . (19.1)

(В случае краевого решения, когда один из двух факторов не используется, условие касания удовлетворяться не должно. Аналогичным образом, если производственная функция имеет " изломы", условие касания теряет смысл. Эти исключения подобны исключениям в ситуации с потребителем, поэтому в настоящей главе мы не будем акцентировать внимание на указанных случаях.)

Алгебра, скрывающаяся за уравнением (19.1), трудностей не представляет. Рассмотрим любое изменение структуры производства (D x ₁, D x ₂), при котором выпуск остается постоянным. Такое изменение должно удовлетворять уравнению:

MP ₁( 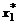, )D x ₁ + MP ₂( 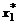, )D x ₂ = 0. (19.2)

Обратите внимание на то, что D x ₁ и D x ₂ должны иметь противоположные знаки; если вы увеличиваете используемое количество фактора 1, то для сохранения выпуска неизменным вам придется уменьшить используемое количество фактора 2.

Если мы находимся в точке минимума издержек, то данное изменение не может привести к снижению издержек, поэтому должно соблюдаться условие:

w ₁D x ₁ + w ₂D x ₂ ≥ 0. (19.3)

Теперь рассмотрим изменение (—D x ₁, —D x ₂), при котором также производится постоянный объем выпуска и издержки также не могут снижаться. Это подразумевает, что

— w ₁D x ₁ — w ₂D x ₂ ≥ 0. (19.4)

Сложив выражения (19.3) и (19.4), получим

w ₁D x ₁ + w ₂D x ₂ = 0. (19.5)

Решение уравнений (19.2) и (19.5) для D x ₂/D x ₁ дает нам

= — = — ,

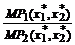а это не что иное, как условие минимизации издержек, выведенное выше путем геометрических рассуждений.

Обратите внимание на некоторое сходство рис. 19.1 с решением задачи потребительского выбора, графически изображенным ранее. Хотя эти решения и выглядят одинаково, на самом деле они относятся к разным задачам. В задаче потребительского выбора прямая являлась бюджетным ограничением, и потребитель в поисках наиболее предпочитаемого положения двигался вдоль бюджетного ограничения. В задаче с производителем изокванта представляет собой технологическое ограничение, и производитель в поисках оптимального положения перемещается вдоль изокванты.

Выбор количеств факторов, минимизирующих издержки фирмы, вообще говоря, зависит от цен факторов и от того объема выпуска, который фирма хочет производить, поэтому мы записываем эти выбранные количества факторов в виде x ₁(w ₁, w ₂, y) и x ₂(w ₁, w ₂, y). Это так называемые функции условного спроса на факторы, или функции производного спроса на факторы. Они показывают взаимосвязь между ценами и выпуском и оптимальный выбор фирмой количества факторов при условии производства фирмой заданного объема выпуска y.

Обратите особое внимание на различие между функциями условного спроса на факторы и функциями спроса на факторы, максимизирующего прибыль, которые были рассмотрены в предыдущей главе. Функции условного спроса на факторы показывают выбор, минимизирующий издержки при заданном объеме выпуска; функции же спроса на факторы, максимизирующего прибыль, показывают выбор, максимизирующий прибыль при заданной цене фактора.

Функции условного спроса на факторы, как правило, не являются непосредственно наблюдаемыми: они представляют собой гипотетическое построение и отвечают на вопрос, сколько каждого фактора использовала бы фирма, если бы хотела произвести заданный объем выпуска самым дешевым способом. Однако функции условного спроса на факторы полезны в качестве способа отделения задачи определения оптимального объема выпуска от задачи определения метода производства, минимизирующего издержки.

ПРИМЕР: Минимизация издержек для случаев конкретных технологий

Предположим, что мы рассматриваем технологию, при которой факторы производства являются совершенными комплементами, так что f (x ₁, x ₂) = = min { x ₁, x ₂}.Тогда, если мы хотим произвести y единиц выпуска, нам явно потребуется y единиц x ₁ и y единиц x ₂. Следовательно, минимальные издержки производства будут равны

c (w ₁, w ₂, y) = w ₁ y + w ₂ y = (w ₁ + w ₂) y.

Что можно сказать о случае технологии с использованием совершенных субститутов f (x ₁, x ₂) = x ₁ + x ₂? Поскольку товары 1 и 2 выступают в производстве совершенными субститутами, ясно, что фирма будет использовать тот из них, который дешевле. Поэтому минимальные издержки производства y единиц выпуска составят w ₁ y или w ₂ y в зависимости от того, какая из этих двух величин меньше. Другими словами:

c (w ₁, w ₂, y) = min{ w ₁ y, w ₂ y } = min{ w ₁, w ₂} y.

Наконец, рассмотрим технологию Кобба—Дугласа, описываемую формулой f (x ₁, x ₂) = . В этом случае мы можем применить технику дифференциального исчисления, чтобы показать, что функция издержек примет вид

c (w ₁, w ₂, y) = K ,

где K есть константа, зависящая от a и от b. Подробности этого исчисления представлены в приложении.