
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства характеристических функций
|
|
В термодинамике существуют два метода исследования макросистем: метод циклов и метод характеристических (термодинамических) функций. Первый метод основан на введении искусственных обратимых циклов при анализе какого-либо вопроса. Типичным примером является построение абсолютной шкалы температур, где искусственно вводится ряд последовательно связанных циклов Карно. Хотя он во всех случаях приводит к правильному решению задачи, его нельзя считать совершенным. Метод циклов требует чисто искусственных построений и обходных путей при решении конкретных задач. Естественно, что с развитием термодинамики он уступил место второму методу, основанному на применении термодинамических функций, дающему гораздо больше возможностей и широко распространенному в настоящее время.
Среди термодинамических функций, число которых достаточно велико, выделяют так называемые характеристические функции, которые обладают тем свойством, что при выбранных параметрах состояния частные производные характеристической функции по параметрам равны тому или иному параметру состояния. Благодаря этому такие производные получают наиболее простое выражение и ясный физический смысл.
Характеристическими функциями состояния называются функции, с помощью которых и посредством их производных разных порядков могут быть явно выражены все термодинамические свойства, в том числе уравнения состояния, уравнения для определения теплоемкостей ср и сv.
Характеристические функции, полностью определяющие все термодинамические свойства системы, называются также термодинамическими потенциалами.
К характеристическим функциям относят: внутреннюю энергию U(p, S), энтальпию I(p, S), изохорно-изотермический потенциал F(T, V) (свободная энергия), изобарно-изотермический потенциал Z(p, T) (свободная энтальпия).
Если эти функции выражены в аналитической форме через независимые параметры системы, то можно в явной форме получить все основные термодинамические величины, характеризующие систему.
Характеристические функции аддитивны - значение их для сложной системы равно сумме значений этих функций для отдельных частей.
Дифференциалы характеристических функций являются полными дифференциалами.
Рассмотрим объединенные уравнения первого и второго законов термодинамики, записанные в виде
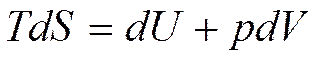 (5.1)
(5.1)
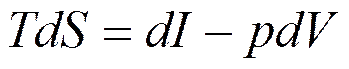 . (5.2)
. (5.2)
Уравнения (5.1) и (5.2) связывают между собой пять переменных величин: T, S, U, p, V, определяющих состояние системы. Из этих пяти параметров можно составить десять различных парных комбинаций: U-T; U-S; U-p; U-V; T-S; T-p; T-V; S-p; S-V; p-V.
Из этих комбинаций для термодинамических исследований большое значение имеют четыре:
U=U(S, V)- внутренняя энергия;
I=(S, p)- энтальпия;
F=F(T, V) - изохорно-изотермический потенциал (свободная энергия);
Z=Z(T, p) - изобарно-изотермический потенциал или изобарный потенциал.
Внутренняя энергия является характеристической функцией при независимых переменных S и V. Запишем уравнение (5.1) в виде
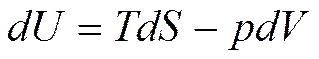 (5.3)
(5.3)
В зависимости от выбранных независимых параметров уравнение (5.3) принимает различный вид. Для вывода этих уравнений в уравнение (5.3) подставляются значения полного дифференциала внутренней энергии при соответствующих независимых параметрах.
Полный дифференциал внутренней энергии при независимых параметрах V и S имеет вид

Подставляя последнее уравнение в (5.3), получим
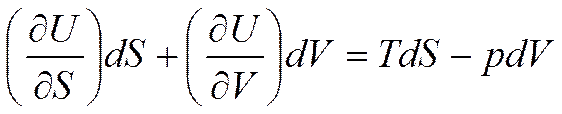
При V=const получим
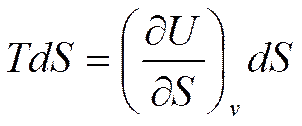
Отсюда
 (5.4)
(5.4)
Аналогично при S=const получим
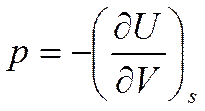 (5.5)
(5.5)
Подставляя (5.5) в формулу для энтальпии I=U+pV, получим
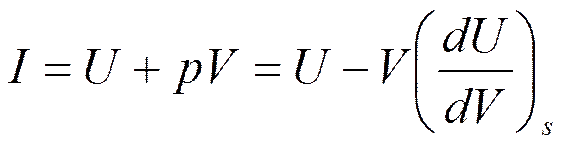
Возьмем производную от (5.4) по S и определим калорические коэффициенты
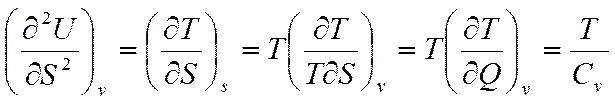
Отсюда
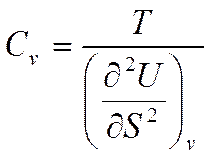 (5.6)
(5.6)
Возьмем производную от (5.5) по V
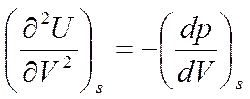
Из уравнений (5.4) и (5.5) путем перекрестного дифференцирования получим
 и
и 
Отсюда
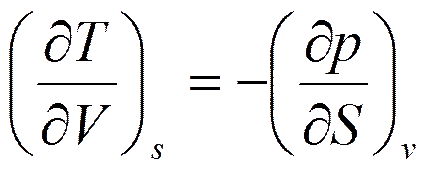 (5.7)
(5.7)
или
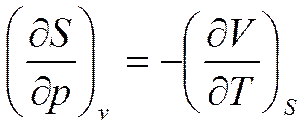 (5.8)
(5.8)
Соотношение (5.8) называется первым соотношением Максвелла.
Таким образом, внутренняя энергия U в переменных S и V является характеристической функцией, с помощью которой можно определить все термодинамические свойства системы. Первые производные определяют термические свойства системы а вторые - калорические.
В термодинамике величины, измеряемые единицами теплоты, принято называть калорическими (внутренняя энергия, энтальпия, энтропия, теплоемкость). К термическим величинам относятся температура, абсолютное давление, удельный объем. Термические величины, в отличие от калорических, могут быть получены непосредственным измерением с помощью приборов.
Следует отметить, что внутренняя энергия является характеристической функцией только в переменных S и V (см. уравнение (5.3)), т.е. U = f(s, V)).
Если внутренняя энергия определяется через любую другую пару параметров, то ее свойства характеристичности утрачиваются, так как в любом другом случае посредством частных производных от внутренней энергии нельзя выразить ни термических, ни калорических свойств веществ.
Энтальпия является характеристической функцией при независимых переменных S и p. Из уравнения (5.2) получим
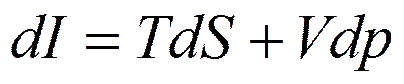 (5.9)
(5.9)
Полный дифференциал энтальпии имеет вид

Подставляя последнее соотношение в (5.9), найдем
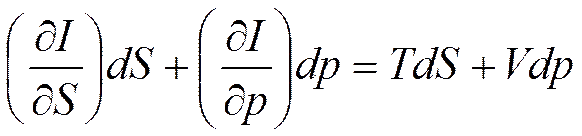
При p=const и S=const соответственно получим
 ;
;  (5.10)
(5.10)
Тогда из формулы I=U+pV будем иметь
 (5.11)
(5.11)
Продифференцируем (5.10) первое по p, второе по S
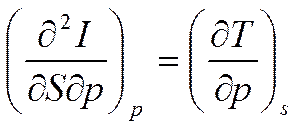 ;
; 
или
 ;
; 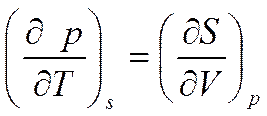 (5.12)
(5.12)
Соотношение (5.12) является вторым соотношением Максвелла.
Продифференцируем первую формулу (5.10) по S
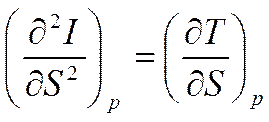
Известно, что
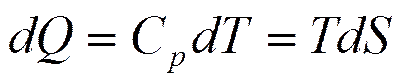
Подставляя в это соотношение выражение для полного дифференциала температуры при независимых переменных S и p

получим
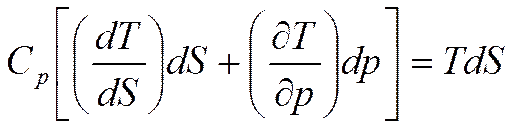
При p=const найдем

или
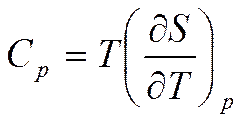 (5.13)
(5.13)
Откуда
 ,
, 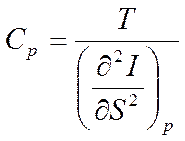
Вычислив вторую производную от второго соотношения (5.10), получим
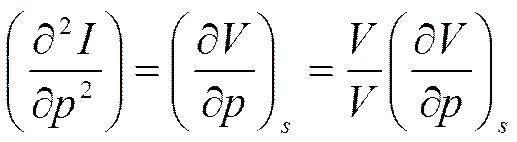
С учетом формулы (2.13) для коэффициента адиабатной сжимаемости  будем иметь
будем иметь
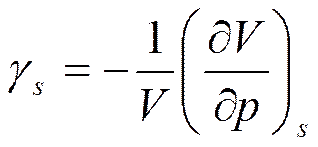
Отсюда
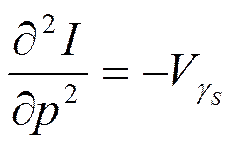
Таким образом, первые частные производные от энтальпии определяют термические параметры - температуру и объем (см. формулы (5.10)), а вторые производные определяют калорические параметры - теплоемкость при постоянном давлении (5.13) и коэффициент адиабатной сжимаемости 
Из уравнения (5.9) следует, что энтальпия является характеристической функцией при условии, если в качестве аргументов выбраны p и S. При других параметрах энтальпия утрачивает свои характеристические свойства, так как посредством ее частных производных нельзя выразить термические и калорические свойства веществ.
Если независимыми переменными являются T и V, то характеристической функцией будет изохорно-изотермический потенциал F. Найдем термические и калорические параметры с помощью этой характеристической функции.
Вычитая из уравнения (5.3) d(TS), получим
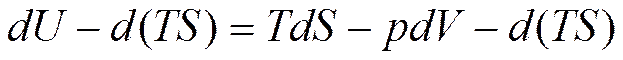 ; (5.14)
; (5.14)
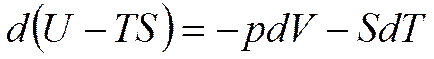 ;
;
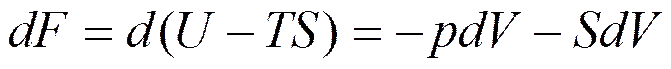 ; (5.15)
; (5.15)
 , или
, или 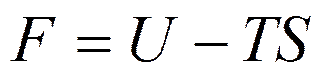 (5.16)
(5.16)
Величину U-TS, являющуюся функцией состояния, называют свободной энергией.
Полный дифференциал изохорно-изотермического потенциала при независимых параметрах V и T имеет вид

Подставляя это соотношение в (5.15), получим

При V=const и T=const соответственно будем иметь
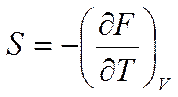 (5.17)
(5.17) 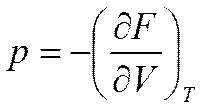 (5.17а)
(5.17а)
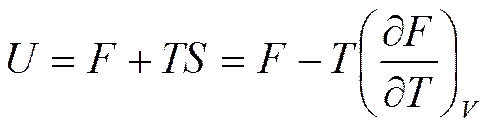 (5.18)
(5.18)
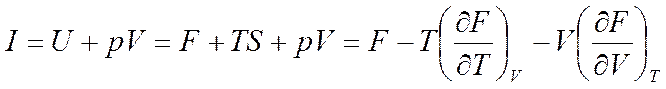 (5.19)
(5.19)
Исходя из (5.17) и (5.17а) составим смешанные вторые производные от F
 ;
; 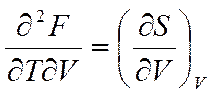
Отсюда
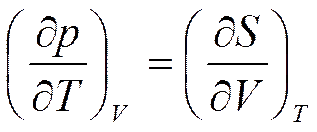 (5.20)
(5.20)
Соотношение (5.20) называется третьим соотношением Максвелла.
Изохорно-изотермический потенциал особенно удобен тем, что независимые переменные V и T легко доступны для измерения.
Из (5.17)
 (5.21)
(5.21)
Подставляя в соотношение  , выражение для полного дифференциала температуры при независимых параметрах S и р, получим
, выражение для полного дифференциала температуры при независимых параметрах S и р, получим

При p=const найдем

Учитывая (5.21), будем иметь
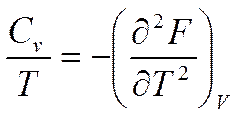
или
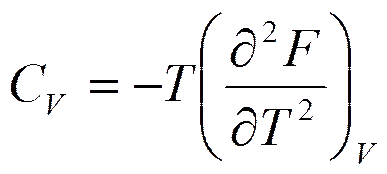
Вычислим вторую производную от (5.17а) по V
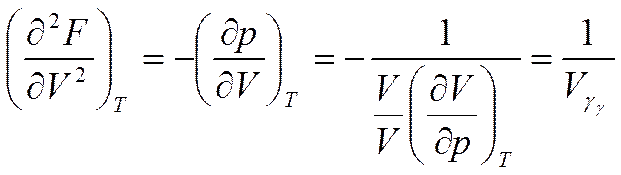
где
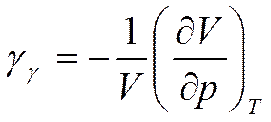
коэффициент изотермической сжимаемости (см. формулу (2.13)).
Таким образом, первые производные от свободной энергии определяют давление р и энтропию S (формулы (5.17), (5.17а)), а вторые производные -теплоемкость при постоянном объеме 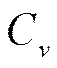 и коэффициент изотермической сжимаемости
и коэффициент изотермической сжимаемости 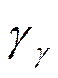
Из уравнения (5.15) следует, что свободная энергия является характеристической функцией только в случае, когда она функция независимых параметров V и T, т.е. F=f(V, T)
Если независимыми параметрами являются Т и р, то характеристической функцией будет изобарный потенциал Z(T, p). Найдем термические и калорические параметры, определяемые через эту характеристическую функцию.
Прибавляя к левой и правой части соотношения (5.15) d(pV), получим
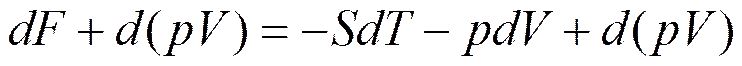 (5.22)
(5.22)
Обозначим dZ=d(F+pV). Так как F=U-TS, то
dZ=d(F+pV)=d(U-TS+pV).
С учетом (5.22) получим
dZ = (U-TS+pV) = -SdT-pdV+pdV+Vdp =
-SdT+Vdp = d(I-TS). (5.23)
Интегрируя, будем иметь
Z=U-TS+pV=I-TS. (5.24)
Подставляя в (5.23) значение полного дифференциала функции Z при T = const и p = const, находим значения других параметров
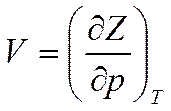 ;
; 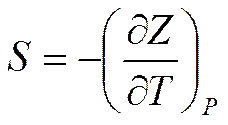 (5.25)
(5.25)
Выразим U из (5.24)
U=Z+TS-pV. (5.26)
Подставляя (5.25) в (5.26), найдем

Выразим энтальпию из (5.24)
I=Z+TS. (5.27)
Подставим (5.25) в (5.27)
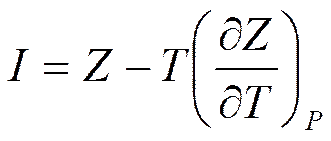
Аналогично

Таким образом, для изобарного потенциала имеем следующие три важнейших формулы
Z=U-TS+pV
Z=I-TS
Z=F+pV
Вычислим вторые производные от (5.25)
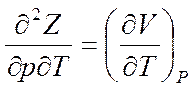 ;
; 

Отсюда
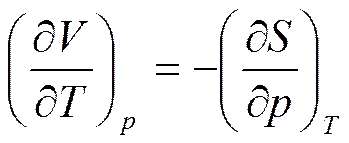 (5.28)
(5.28)
Соотношение (5, 28) представляет собой четвертое соотношение Максвелла.
Вычислим производную от S по T в (5.25)
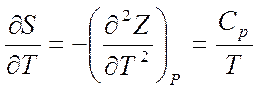
Из последнего соотношения можно найти теплоемкость 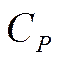
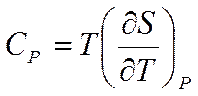
Таким образом, получена формула для Ср, аналогичная формуле (5.13).
Возьмем вторую производную по р от первого соотношения (5.25)
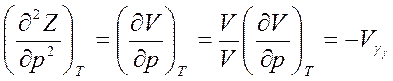
Таким образом, первые производные от изобарного потенциала определяют энтропию S и объем V, а вторые - теплоемкость 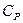 и коэффициент изотермической сжимаемости
и коэффициент изотермической сжимаемости 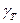 .
.
Уравнение (5.23) свидетельствует о том, что изобарный потенциал обладает характеристическими свойствами лишь в том случае, если независимыми параметрами являются давление p и температура Т, т.е. Z=f(p, T).
Ввиду того, что свободная энергия и изобарный потенциал определяются через легко измеряемые величины (свободная энергия через V, T и изобарный потенциал через p, T), они получили наибольшее применение по сравнению с внутренней энергией и энтальпией, в которые входит не измеряемая опытным путем энтропия.
Уравнения Максвелла имеют большое значение в термодинамике. К тому же они допускают обобщение на случай, когда тело подвергается не механическому, а электрическому, магнитному или какому-либо другому воздействию. В данном случае для обобщения уравнений величины V и p заменяются на обобщенную силу X и обобщенную координату у. Уравнения Максвелла (5.8), (5.12), (5.20), (5.28) принимают соответственно вид
 ;
; 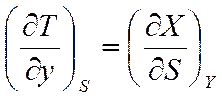 ;
;
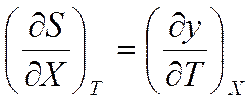 ;
; 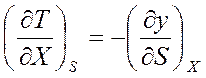
Уравнения Максвелла, в основе которых лежат первый и второй законы термодинамики, являются наиболее общими выражениями, определяющими изменения термодинамических свойств веществ в различных процессах.
|
|