
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Порядок исследования состояния покоя механической системы на устойчивость.
|
|
Выбирается обобщенная координата. Записывается потенциальная энергия как функция обобщенной координаты. Находится первая и вторая производные по обобщенным координатам и выясняется, имеет ли потенциальная энергия в заданном положении минимум.
Колебательное движение материальной точки. Восстанавливающая сила (сила упругости)  , сила стремится вернуть точку в равновесное положение, " с" – коэффициент жесткости пружины = силе упругости при деформации, равной единице [Н/м].
, сила стремится вернуть точку в равновесное положение, " с" – коэффициент жесткости пружины = силе упругости при деформации, равной единице [Н/м].
Свободные колебания  ; обозначив
; обозначив  , получаем
, получаем 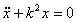 – линейное однородное диффер-ное уравнение второго порядка, характеристическое уравнение:
– линейное однородное диффер-ное уравнение второго порядка, характеристическое уравнение:  , его корни мнимые, отсюда общее решение дифф-ного уравнения будет
, его корни мнимые, отсюда общее решение дифф-ного уравнения будет  , C 1, C 2 – постоянные интегрирования. Для их определения находим уравнение скоростей:
, C 1, C 2 – постоянные интегрирования. Для их определения находим уравнение скоростей:  , подставляем начальные условия в уравнения для х и
, подставляем начальные условия в уравнения для х и  , откуда
, откуда  ,
,  , т.е.
, т.е. 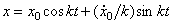 .
.

Можно обозначить  ,
,  отсюда
отсюда  – уравнение гармонических колебаний.
– уравнение гармонических колебаний.  –амплитуда,
–амплитуда,  ,
, 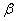 – начальная фаза свободных колебаний;
– начальная фаза свободных колебаний;  – циклическая частота (угловая, собственная) колебаний; период колебаний:
– циклическая частота (угловая, собственная) колебаний; период колебаний:  , где k и Т не зависят от начальных условий – изохронность колебаний; амплитуда и начальная фаза зависят о начальных условий. Под действием постоянной силы Р происходит смещение центра колебаний в сторону действия силы Р на величину статического отклонения
, где k и Т не зависят от начальных условий – изохронность колебаний; амплитуда и начальная фаза зависят о начальных условий. Под действием постоянной силы Р происходит смещение центра колебаний в сторону действия силы Р на величину статического отклонения  . Если Р – сила тяжести, то
. Если Р – сила тяжести, то  .
.
Затухающие колебания при действии  сила сопротивления, пропорциональная скорости (вязкое трение).
сила сопротивления, пропорциональная скорости (вязкое трение).  , обозначив
, обозначив  , получаем:
, получаем:
 , характеристическое уравнение:
, характеристическое уравнение:  , его корни:
, его корни:  . а) При n< k корни мнимые, отсюда общее решение дифф.ур-ия имеет вид:
. а) При n< k корни мнимые, отсюда общее решение дифф.ур-ия имеет вид:  , обозначив
, обозначив  ,
,  имеем
имеем  . Множитель
. Множитель  показывает, что колебания затухающие. График заключен между двумя симметричными относительно оси t кривыми
показывает, что колебания затухающие. График заключен между двумя симметричными относительно оси t кривыми  . Из начальных условий:
. Из начальных условий:  ,
,  ; частота затухающих колебаний:
; частота затухающих колебаний:  ; период:
; период:  , период затухающих колебаний больше периода свободных колебаний (при небольших сопротивлениях
, период затухающих колебаний больше периода свободных колебаний (при небольших сопротивлениях  ). Амплитуды колебаний уменьшаются:
). Амплитуды колебаний уменьшаются:  – декремент колебаний;
– декремент колебаний;  логарифмический декремент; " n" – коэффициент затухания.
логарифмический декремент; " n" – коэффициент затухания.

Апериодическое движение точки при  или
или 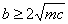 . При
. При  корни характеристич-ого ур-я вещественны, общее решение:
корни характеристич-ого ур-я вещественны, общее решение:  , обозначая
, обозначая  ,
,  ,
,  (ch, sh – гиперболические косинус и синус), если ввести
(ch, sh – гиперболические косинус и синус), если ввести  ,
,  , то
, то  – это уравнение не колебательного движения (апериодического), т.к. гиперболический синус не является периодической функцией. При
– это уравнение не колебательного движения (апериодического), т.к. гиперболический синус не является периодической функцией. При  корни характеристич. ур-я вещественны, равны и отрицательны:
корни характеристич. ур-я вещественны, равны и отрицательны:  , общее решение:
, общее решение:  , или
, или  , движение также апериодическое.
, движение также апериодическое.

Вынужденные колебания кроме восстанавливающей силы действует переменная возмущающая сила, обычно, по гармоническому закону:  , р – частота возмущающей силы,
, р – частота возмущающей силы,  – начальная фаза.
– начальная фаза.  ,
,  ,
,  – дифференциальное уравнение вынужденных колебаний (неоднородное линейное дифф-ное ур-ие). Его общее решение = сумме общего решения однородного уравнения
– дифференциальное уравнение вынужденных колебаний (неоднородное линейное дифф-ное ур-ие). Его общее решение = сумме общего решения однородного уравнения  и частного решения данного уравнения:
и частного решения данного уравнения:  , где
, где 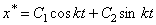 ,
,  – частное решение ищется в виде подобном правой части уравнения. Подставляя решение в уравнение, находим
– частное решение ищется в виде подобном правой части уравнения. Подставляя решение в уравнение, находим  ,
, 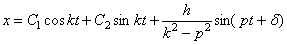 . Величина статического отклонения:
. Величина статического отклонения:  ,
,  – коэфф-нт динамичности, во сколько раз амплитуда колебаний превосходит статическое отклонение.
– коэфф-нт динамичности, во сколько раз амплитуда колебаний превосходит статическое отклонение.
|
|