
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Точки разрыва функции
|
|
Если требования непрерывности функции в точке  не выполняются, т.е. функция не определена в точке
не выполняются, т.е. функция не определена в точке 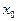 или предел функции в точке
или предел функции в точке  не существует, или существует, но не равен значению функции в этой точке, то функция называется разрывной в точке
не существует, или существует, но не равен значению функции в этой точке, то функция называется разрывной в точке  , а сама точка
, а сама точка  называется точкой разрыва функции.
называется точкой разрыва функции.
Если функция имеет предел в точке  , но он не совпадает со значением функции в этой точке или функция не определена в этой точке, то разрыв называется устранимым.
, но он не совпадает со значением функции в этой точке или функция не определена в этой точке, то разрыв называется устранимым.
Если функция имеет в точке  односторонние пределы, не равные между собой, то
односторонние пределы, не равные между собой, то  называется точкой разрыва первого рода. При этом
называется точкой разрыва первого рода. При этом 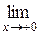
 –
– 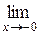
 =
=  называется скачком функции в точке
называется скачком функции в точке  .
.
Если хотя бы один из односторонних пределов не существует или бесконечный в точке 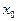 , то эта точка разрыва второго рода.
, то эта точка разрыва второго рода.
Итак, функция  терпит разрыв в точке
терпит разрыв в точке  в одном из следующих случаев:
в одном из следующих случаев:
1)  , но
, но  , либо
, либо  не определено (рис.1); в этом случае говорят, что
не определено (рис.1); в этом случае говорят, что  – точка устранимого разрыва;
– точка устранимого разрыва;
2)  – конечные, но не равные между собой пределы; такая точка называется точкой разрыва первого рода (говорят, что
– конечные, но не равные между собой пределы; такая точка называется точкой разрыва первого рода (говорят, что  терпит в точке
терпит в точке  скачок) (рис.2);
скачок) (рис.2);
3) по крайней мере одного из односторонних пределов  в точке
в точке  не существует (т.е. не существует конечного предела); в таком случае говорят, что x0 – точка разрыва второго рода (рис.3).
не существует (т.е. не существует конечного предела); в таком случае говорят, что x0 – точка разрыва второго рода (рис.3).
 Рис.1
Рис.1
|  Рис.2
Рис.2
|
 Рис. 3
Рис. 3
|
Если функция непрерывна в каждой точке интервала ( ,
,  ), то она называется непрерывной на этом интервале. Если
), то она называется непрерывной на этом интервале. Если 
 =
=  , то функция называется непрерывной в точке
, то функция называется непрерывной в точке  слева. Аналогично при
слева. Аналогично при 
 =
=  – непрерывной в точке
– непрерывной в точке  справа.
справа.
Если функция непрерывна в каждой точке интервала ( ,
,  ),
),  <
<  и в точке
и в точке  =
=  она непрерывна справа, а в точке
она непрерывна справа, а в точке  =
=  – слева, то она называется непрерывной на отрезке [
– слева, то она называется непрерывной на отрезке [  ,
,  ].
].
Все основные элементарные функции непрерывны в своих областях определения. Напомним, что под основными элементарными функциями понимают следующие пять функций:
1) степенную  =
=  ,
,  Î R;
Î R;
2) показательную  =
=  ,
,  > 0,
> 0,  ¹ 1;
¹ 1;
3) логарифмическую  =
=  ,
,  > 0,
> 0,  > 0,
> 0,  ¹ 1;
¹ 1;
4) тригонометрические  = sin
= sin  ,
,  = cos
= cos  ;
;
5)  обратные тригонометрические
обратные тригонометрические  = arcsin
= arcsin  ,
,  Î [–1, 1],
Î [–1, 1], 

|
|