
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение производной.
|
|
Рассмотрим функцию  , определенную на некотором промежутке X. Возьмем любую точку
, определенную на некотором промежутке X. Возьмем любую точку  и зададим аргументу x в точке
и зададим аргументу x в точке  произвольное приращение
произвольное приращение  такое, что точка
такое, что точка  +
+  также принадлежит Х.
также принадлежит Х.  Функция получит приращение
Функция получит приращение 
 +
+  ) –
) –  .
.
Производной функции  в точке
в точке  называется предел отношения приращения функции в этой точке к приращению аргумента при
называется предел отношения приращения функции в этой точке к приращению аргумента при  (при условии, что этот предел существует).
(при условии, что этот предел существует).
Производная обозначается  ,
,  ,
, 
Итак, по определению, 
Если для некоторого значения  выполняется условие
выполняется условие 
 или (
или ( ), то говорят, что в точке
), то говорят, что в точке  функция имеет бесконечную производную знака плюс (или знака минус). В отличие от бесконечной производной, определенную выше производную функции иногда называют конечной производной.
функция имеет бесконечную производную знака плюс (или знака минус). В отличие от бесконечной производной, определенную выше производную функции иногда называют конечной производной.
Функция  , имеющая производную в каждой точке промежутка называется дифференцируемой на этом промежутке. Операция нахождение производной функции называется дифференцированием функции.
, имеющая производную в каждой точке промежутка называется дифференцируемой на этом промежутке. Операция нахождение производной функции называется дифференцированием функции.
Пример 1. Найдем производную функции  .
.
Придав аргументу  приращение
приращение  , находим приращение функции
, находим приращение функции  :
:  Составим отношение:
Составим отношение:  . Тогда, по определению производной
. Тогда, по определению производной
 .
.
При вычислении предела воспользовались эквивалентностью  ~
~  при
при 
Итак,  , т.е.
, т.е. 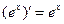 .
.
Аналогично, используя определение производной, можно вывести формулы производных основных элементарных функций:
1. Степенная функция  ,
, 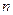 – любое действительное число.
– любое действительное число.
 ,
,  .
.
2. Показательная функция 
 > 0.
> 0.
 ,
, 
3. Логарифмическая функция  ,
,  > 0,
> 0,  1.
1.
 ,
, 
 ,
,  .
.
4. Тригонометрические функции.
 ,
, 
 ,
, 
 ,
, 
Теорема. Если функция  дифференцируема в данной точке х, то она непрерывна в этой точке.
дифференцируема в данной точке х, то она непрерывна в этой точке.
Таким образом, в точках разрыва функция не может иметь производной.
Замечание. Обратное не верно, т.е. из непрерывности функции  в некоторой точке х не следует дифференцируемость функции в этой точке.
в некоторой точке х не следует дифференцируемость функции в этой точке.
Таким образом, в данном учебном вопросе мы познакомились с понятием производной, научились находить производные основных элементарных функций.
Вопрос 2. Геометрический и физический смысл производной
Пусть некоторая материальная точка (тело) движется неравномерно по некоторой прямой.

Рис. 1
Расстояние s движущейся точки  , отсчитываемое от некоторого начального ее положения
, отсчитываемое от некоторого начального ее положения  будет зависеть от времени t, т.е. s функция времени t:
будет зависеть от времени t, т.е. s функция времени t:  =
=  . Это равенство называют законом движения точки (рис.1).
. Это равенство называют законом движения точки (рис.1).
Пусть в некоторый момент времени t точка  находилась на расстоянии s от начального положения
находилась на расстоянии s от начального положения  , а в некоторый следующий момент
, а в некоторый следующий момент  (
( – приращение времени) точка оказалась в положении
– приращение времени) точка оказалась в положении  на расстоянии
на расстоянии  от начального положения. Таким образом, за промежуток
от начального положения. Таким образом, за промежуток  величина s получила приращение
величина s получила приращение  ,
,  . Отношение
. Отношение  выражает среднюю скорость движения точки за время t. То есть,
выражает среднюю скорость движения точки за время t. То есть,  . Для того, чтобы точнее выразить истинную скорость с помощью средней скорости, надо взять меньший промежуток времени
. Для того, чтобы точнее выразить истинную скорость с помощью средней скорости, надо взять меньший промежуток времени  . Наиболее полно характеризует скорость движения точки в момент t тот предел к которому стремится средняя скорость при
. Наиболее полно характеризует скорость движения точки в момент t тот предел к которому стремится средняя скорость при 
 . Этот предел называют скоростью движения в данный момент времени
. Этот предел называют скоростью движения в данный момент времени  или
или  .
.
Скоростью движения в данный момент называется предел отношения приращения пути  к приращению времени
к приращению времени  , когда приращение времени стремится к 0. То есть, скорость прямолинейного движения материальной точки в момент времени t есть производная от пути s по времени t:
, когда приращение времени стремится к 0. То есть, скорость прямолинейного движения материальной точки в момент времени t есть производная от пути s по времени t:  В этом заключается механический смысл производной.
В этом заключается механический смысл производной.
В общем случае, если функция  описывает какой-либо физический процесс, то производная
описывает какой-либо физический процесс, то производная  есть скорость протекания этого процесса. В этом состоит физический смысл производной.
есть скорость протекания этого процесса. В этом состоит физический смысл производной.
Теперь дадим геометрическое истолкование производной. Для этого потребуется определение касательной к кривой в данной точке.
Пусть имеем кривую 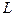 и на ней точки
и на ней точки  и
и  .Проведем прямую, проходящую через эти точки. Она называется секущей. Пусть точка
.Проведем прямую, проходящую через эти точки. Она называется секущей. Пусть точка  неограниченно приближается по кривой к точке
неограниченно приближается по кривой к точке  . Тогда секущая, поворачиваясь около точки
. Тогда секущая, поворачиваясь около точки  стремится к некоторому предельному положению
стремится к некоторому предельному положению  .
.
Касательной кданной кривой в данной точке  называется предельное положение
называется предельное положение  секущей
секущей  , проходящей через точку
, проходящей через точку  , когда вторая точка пересечения
, когда вторая точка пересечения  неограниченно приближается по кривой к точке
неограниченно приближается по кривой к точке  (рис. 2).
(рис. 2).
 |
Рис. 2
Рассмотрим теперь график непрерывной функции  , имеющий в точке
, имеющий в точке  невертикальную касательную.
невертикальную касательную.
Пусть при некоторых значениях  функция имеет значение
функция имеет значение  . Этому значению соответствует точка
. Этому значению соответствует точка  . Дадим аргументу
. Дадим аргументу  приращение
приращение  . Новому значению аргумента
. Новому значению аргумента  соответствует значение функции
соответствует значение функции  . Соответствующей точкой графика будет точка
. Соответствующей точкой графика будет точка 
 . Проведем секущую
. Проведем секущую  и обозначим через
и обозначим через  угол, образованный секущей и положительным направлением оси Оx (рис.3). Составим отношение
угол, образованный секущей и положительным направлением оси Оx (рис.3). Составим отношение  .
.
Из рисунка 3 видно, что  . Если
. Если  , то точка
, то точка  стремится к точке
стремится к точке  . Секущая
. Секущая  будет поворачиваться, угол
будет поворачиваться, угол  будет меняться. Если при
будет меняться. Если при  , угол
, угол  стремится к некоторому пределу
стремится к некоторому пределу  , то прямая, проходящая через точку
, то прямая, проходящая через точку  и составляющая с положительным направлением оси Оx угол
и составляющая с положительным направлением оси Оx угол  будет искомой касательной. Найдем ее угловой коэффициент:
будет искомой касательной. Найдем ее угловой коэффициент:

 .
.
 |
Рис. 3
Таким образом, мы получили, что значение производной  при данном значении аргумента х равняется тангенсу угла, образованного с положительным направлением оси Оx касательной к графику функции
при данном значении аргумента х равняется тангенсу угла, образованного с положительным направлением оси Оx касательной к графику функции  в соответствующей точке
в соответствующей точке  , или, другими словами, производная равна угловому коэффициенту. В этом состоит геометрический смысл производной.
, или, другими словами, производная равна угловому коэффициенту. В этом состоит геометрический смысл производной.
|
|