
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры решения типовых задач
|
|
Пример 1. Доказать  .
.
Решение: Рассмотрим величину:

 .
.
Пусть  – произвольное число, выберем
– произвольное число, выберем  ; тогда если
; тогда если  , то
, то  , следовательно,
, следовательно,  .
.
Таким образом, по определению,  .
.
Пример 2. Вычислить  .
.
Решение. Используя свойства предлов функций, получим:

 .
.
Пример 3. Вычислить  .
.
Решение.
 .
.
Чтобы раскрыть неопределенность вида  , заданную отношением двух многочленов, надо в числителе и в знаменателе выделить множитель, равный нулю при предельном значении
, заданную отношением двух многочленов, надо в числителе и в знаменателе выделить множитель, равный нулю при предельном значении 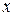 , и сократить на него.
, и сократить на него.
Пример 4. Вычислить  .
.
Решение. Подставляя предельное значение  в числитель и знаменатель, получаем, что оба выражения обращаются при этом в нуль. Имеем неопределенность вида
в числитель и знаменатель, получаем, что оба выражения обращаются при этом в нуль. Имеем неопределенность вида  . Стоящие в числителе и знаменателе многочлены можно разложить на множители. Следует помнить, что если
. Стоящие в числителе и знаменателе многочлены можно разложить на множители. Следует помнить, что если  ,
,  – корни квадратного трехчлена
– корни квадратного трехчлена  , то справедлива формула
, то справедлива формула
 .
.
Таким образом, имеем:
 .
.
Пример 5. Вычислить 
Решение. Имеет место неопределенность вида  . Так как
. Так как  является корнем многочленов из числителя и знаменателя, то
является корнем многочленов из числителя и знаменателя, то  выделяется как сомножитель в числителе и знаменателе.
выделяется как сомножитель в числителе и знаменателе.
 .
.
Чтобы раскрыть неопределенность вида  , в которой числитель или знаменатель содержит иррациональность, следует соответствующим образом избавиться от нее (например, умножить на сопряженное выражение или ввести новую переменную).
, в которой числитель или знаменатель содержит иррациональность, следует соответствующим образом избавиться от нее (например, умножить на сопряженное выражение или ввести новую переменную).
Пример 6. Вычислить  .
.
Решение. Подставляя предельное значение  в числитель и знаменатель, получаем неопределенность вида
в числитель и знаменатель, получаем неопределенность вида  . Знаменатель представляет собой «сумму кубов», поэтому при разложении его на множители получаем:
. Знаменатель представляет собой «сумму кубов», поэтому при разложении его на множители получаем:  . После умножения числителя и знаменателя на сопряженное числителю выражение
. После умножения числителя и знаменателя на сопряженное числителю выражение  , имеем:
, имеем:


 .
.
Пример 7. Вычислить 
Решение. Имеет место неопределенность вида  . Произведем замену
. Произведем замену  Тогда при
Тогда при  имеем
имеем 


Чтобы раскрыть неопределенность вида  , заданную отношением двух многочленов, надо числитель и знаменатель разделить на самую высокую степень
, заданную отношением двух многочленов, надо числитель и знаменатель разделить на самую высокую степень 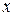 , а затем перейти к пределу.
, а затем перейти к пределу.
Пример 8. Вычислить 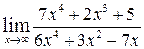 .
.
Решение. Имеем неопределенность вида  . Для ее раскрытия можно либо разделить числитель и знаменатель на наибольшую степень переменной x и, учитывая, что величина обратная бесконечно большой величине есть бесконечно малая величина, раскрыть исходную неопределенность, либо вынести переменную в наибольшей степени в числителе и знаменателе дроби и сократить на наибольшую степень.
. Для ее раскрытия можно либо разделить числитель и знаменатель на наибольшую степень переменной x и, учитывая, что величина обратная бесконечно большой величине есть бесконечно малая величина, раскрыть исходную неопределенность, либо вынести переменную в наибольшей степени в числителе и знаменателе дроби и сократить на наибольшую степень.
 .
.
Пример 9. Вычислить  .
.
Решение. Имеем неопределенность вида  . Раскрываем ее аналогично тому, как это сделано в примере 8.
. Раскрываем ее аналогично тому, как это сделано в примере 8.
 .
.
Пример 10. Вычислить  .
.
Решение. Имеем неопределенность вида  . Раскрываем ее аналогично тому, как это сделано в примере 8.
. Раскрываем ее аналогично тому, как это сделано в примере 8.
 .
.
Пример 11. Вычислить 
Решение. Имеем неопределенность вида  . Избавимся от нее следующим образом: разделим числитель и знаменатель на степень с наивысшим основанием, т.е. на
. Избавимся от нее следующим образом: разделим числитель и знаменатель на степень с наивысшим основанием, т.е. на  . Затем воспользуемся равенством
. Затем воспользуемся равенством  если
если 

Пример 12. Вычислить  .
.
Решение. Очевидно, что при 
 и
и 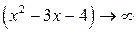 . Поэтому имеем неопределенность вида
. Поэтому имеем неопределенность вида  . Далее получаем:
. Далее получаем:
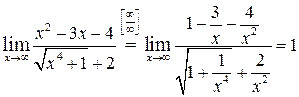 .
.
Неопределенности вида  возникают, как правило, либо при исследовании разности двух дробей (в этом случае рекомендуется приводить дроби к общему знаменателю), либо при рассмотрении разности иррациональных выражений (для избавления от иррациональностей следует преобразовать исходное выражение либо к разности квадратов, либо к сумме или разности кубов).
возникают, как правило, либо при исследовании разности двух дробей (в этом случае рекомендуется приводить дроби к общему знаменателю), либо при рассмотрении разности иррациональных выражений (для избавления от иррациональностей следует преобразовать исходное выражение либо к разности квадратов, либо к сумме или разности кубов).
Пример 13. Вычислить  .
.
Решение. В данном случае имеем неопределенность  . Приведем дроби к общему знаменателю:
. Приведем дроби к общему знаменателю:
 .
.
Пример 14. Вычислить  .
.
Решение. В данном случае, чтобы раскрыть неопределенность  , необходимо умножить и разделить рассматриваемое выражение на «сопряженное», чтобы прийти к разности квадратов. Для
, необходимо умножить и разделить рассматриваемое выражение на «сопряженное», чтобы прийти к разности квадратов. Для  таким «сопряженным» является
таким «сопряженным» является  . Таким образом, получаем:
. Таким образом, получаем:

 .
.
Таким образом, мы попали в ситуацию, разобранную при решении примера 12. Проведем соответствующие преобразования в знаменателе:
 .
.
При вычислении пределов, содержащих тригонометрические функции, полезно использовать «первый замечательный предел»  .
.
Пример 15. Вычислить  .
.
Решение. Очевидно, что при  ,
,  и
и  . Чтобы применить первый замечательный предел, необходимо получить в знаменателе выражение, совпадающие с аргументом синуса. Для этого числитель и знаменатель умножаем на число 4:
. Чтобы применить первый замечательный предел, необходимо получить в знаменателе выражение, совпадающие с аргументом синуса. Для этого числитель и знаменатель умножаем на число 4:
 .
.
Пример 16. Вычислить  .
.
Решение. Знаменатель разложим на множители как разность квадратов, а в числителе воспользуемся формулой  :
:

 .
.
Пример 17. Вычислить  .
.
Решение. В данном случае, чтобы раскрыть неопределенность  , можно воспользоваться формулой
, можно воспользоваться формулой  :
:


В примерах с неопределенностью  выражение, стоящее под знаком предела представляет собой показательно–степенную функцию. Неопределенность устраняется при помощи выделения «второго замечательного предела»
выражение, стоящее под знаком предела представляет собой показательно–степенную функцию. Неопределенность устраняется при помощи выделения «второго замечательного предела»  .
.
Пример 18. Вычислить  .
.
Решение. Имеем неопределенность вида  . Для раскрытия этой неопределенности воспользуемся вторым замечательным пределом:
. Для раскрытия этой неопределенности воспользуемся вторым замечательным пределом:


 .
.
Пример 19. Найти предел функции 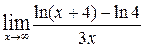 .
.
Решение. Имеем неопределенность вида  , преобразуем ее к неопределенности вида
, преобразуем ее к неопределенности вида  . Пользуясь свойствами логарифмов:
. Пользуясь свойствами логарифмов:  и
и  , получим:
, получим:
 .
.
Далее
 .
.
Пример 20. Найти предел функции  .
.
Решение. В данном примере при выяснении вида неопределенности видим, что таковой не имеется. Имеем  , тогда
, тогда  .
.
Пример 21. Найти предел функции  .
.
Решение. Имеем неопределенность вида  . Для раскрытия этой неопределенности воспользуемся вторым замечательным пределом
. Для раскрытия этой неопределенности воспользуемся вторым замечательным пределом  :
:
 .
.
Пример 22. Найти предел функции  .
.
Решение. Выделим в числителе, выражение вида  , а в знаменателе –
, а в знаменателе –  . Затем воспользуемся следующим равенствами
. Затем воспользуемся следующим равенствами  и
и  :
:
 .
.
Задания для самостоятельной работы
n 19. Доказать равенство.
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 20. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  ; ;
|
n 21. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 22. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 23. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е) 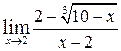 ; ;
|
ж) 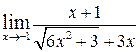 ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 24. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 25. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 26. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 27. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 28. Вычислить
а) 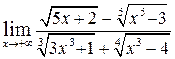 ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д) 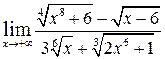 ; ;
| е)  ; ;
|
ж) 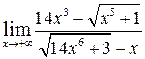 ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 29. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 30. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 31. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 32. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г) 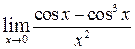 ; ;
|
д)  ; ;
| е)  ; ;
|
ж) 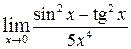 ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 33. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 34. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 35. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 36. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е) 
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к) 
|
|
|