
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Второй замечательный предел.
|
|
 =е (1) (неопределенность 1±¥ )
=е (1) (неопределенность 1±¥ )
Число е (число Эйлера) - иррационально.
1) Докажем, что если  =+¥, то
=+¥, то  = е.
= е.
а) Рассмотрим случай, когда все значения переменной хm являются целыми положительными числами. Возьмем e> 0 – любое, сколь угодно малое.
Было доказано, что  = е. Значит, взятому e> 0 отвечает номер Nтакой, что для всех n> NÞ
= е. Значит, взятому e> 0 отвечает номер Nтакой, что для всех n> NÞ  < e.
< e.
По условию  =+¥, поэтому $МÎ N: " m> MÞ xm> N. По предположению все значения переменной xm – натуральные числа. Поэтому " m> MÞ
=+¥, поэтому $МÎ N: " m> MÞ xm> N. По предположению все значения переменной xm – натуральные числа. Поэтому " m> MÞ  < e.
< e.
А это означает, что  = е. (В рассмотренном случае переменная xm не обязательно монотонно возрастающая).
= е. (В рассмотренном случае переменная xm не обязательно монотонно возрастающая).
б) Пусть значения переменной xm положительные числа, не обязательно целые, > 2.
Пусть am – наибольшее натуральное число, удовлетворяющее неравенству am£ xm. Тогда am³ 2 и am®+¥ при xm®+¥. Имеем
am-1< xm< am+1Þ  >
>  >
>  Þ 1+
Þ 1+  > 1+
> 1+  > 1+
> 1+ 
Тогда  >
> 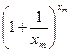 >
>  (*)
(*)
Имеем 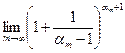 =
= 
 =е× 1=е.
=е× 1=е.
Тогда из (*) по теореме о пределе промежуточной последовательности,  = е.
= е.
2) Покажем, что  = е. Воспользуемся определением предела функции по Гейне.
= е. Воспользуемся определением предела функции по Гейне.
Составим последовательность х1, …, хn - любую, но такую, чтобы xn> 2 и xn®+¥, n®¥.
Соответствующая последовательность значений функции будет такой:
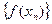 =
=  . Было показано, что
. Было показано, что  =е.
=е.
Т.к. {xn} – любая последовательность, удовлетворяющая условиям xn> 2 и xn®+¥, n®¥, то в соответствии с определением предела функции по Гейне,  = е.
= е.
3) Покажем, что  = е.
= е.
Составим последовательность х1, х2, …, хn - любую, но такую, чтобы xn< -3 и xn®-¥, n®¥. Если положить xn=-1-yn, то yn®+¥, n®¥ (и все yn> 2). Имеем
 =
=  =
=  =
=  =
= 

Т.к.  =е, а
=е, а  =1, то
=1, то  =
= 
 =е.
=е.
Т.к. {xn} – любая последовательность, удовлетворяющая условиям xn< -3 и xn®-¥, n®¥, то в соответствии с определением предела функции по Гейне,  = е.
= е.
Сделав в  замену переменной х на
замену переменной х на  . Получим функцию
. Получим функцию  .
.
Составим последовательность {an} - любую, но такую, чтобы an> 0 и an®0, n®¥. Тогда xn=  ®+¥, n®¥ и, следовательно
®+¥, n®¥ и, следовательно  =
=  =e
=e
Это значит, что  =e.
=e.
Составим последовательность {an} - любую, но такую, чтобы an< 0 и an®0, n®¥. Тогда xn=  ®-¥, n®¥ и, следовательно
®-¥, n®¥ и, следовательно  =
=  =e
=e
Это значит, что  =e.
=e.
Т.к. правый и левый пределы функции  в точке a=0 существуют и равны е, то у этой функции существует обычный (двусторонний) предел и он равен е.
в точке a=0 существуют и равны е, то у этой функции существует обычный (двусторонний) предел и он равен е.
Т.о.  =е. ч.т.д.
=е. ч.т.д.
График функции у=ех – экспонента. Пример. 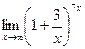 =е21
=е21
|
|