
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример 3.6.
|
|
Пусть в результате наблюдения за экономическим процессом получен ряд из пяти пар чисел 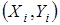 , характеризующих (описывающих) данный процесс (X – объясняющая переменная, причина; Y – объясняемая переменная, следствие):
, характеризующих (описывающих) данный процесс (X – объясняющая переменная, причина; Y – объясняемая переменная, следствие):
| X (причина) | 1, 0 | 1, 5 | 3, 0 | 4, 5 | 5, 0 |
| Y (следствие) | 1, 25 | 1, 4 | 1, 5 | 1, 75 | 2, 25 |
Например, Х – цена предложения товара (грн./шт.), Y – объем предложения товара (тыс.грн.).
Поскольку переменных две, а характер поведения рассматриваемого процесса неизвестен – построим на основе этих эмпирических данных корреляционное поле в декартовой системе координат (рис.3.2).
Корреляционное поле (точечный график; точечная диаграмма рассеивания) – это графическое изображение совокупности реальных статистических данных (данных наблюдений) в виде точек в декартовой системе координат.

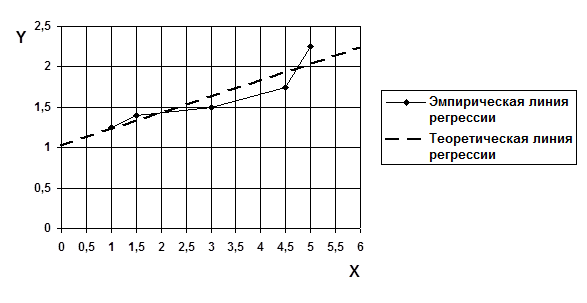
Рис.3.2. Корреляционное поле, эмпирическая и теоретическая линии регрессии
Если на корреляционном поле соединить все точки в порядке возрастания Х отрезками прямой получим эмпирическую (наблюдаемую) линию регрессии.
Причем, если в массиве наблюдений некоторому значению X соответствует несколько значений Y, то только для построения эмпирической линии регрессии при каждом таком Х должно быть определено групповое среднее значение Y. Поэтому в общем случае эмпирическая линия регрессии строится по групповым средним значениям Y, которые определены при имеющих место в массиве наблюдений значениях Х, т.е. необходимо поступать так, как в качестве примера показано на рис.3.3.
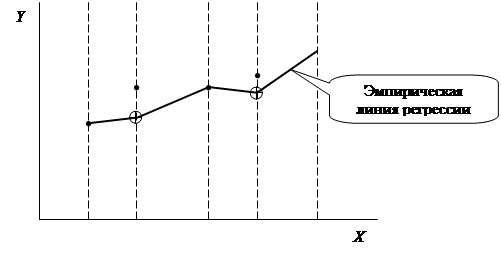 |
Рис.3.3. К методике построения эмпирической линии регрессии
Характер эмпирической линии (в общем случае – поверхности) регрессии дает представление об ожидаемом поведении среднего значения Y под влиянием фактора X (в общем случае – под влиянием учтенных факторов).
Статистические данные, представленные в числовом виде (в виде таблицы значений), не всегда удобны и наглядны. Они значительно лучше воспринимаются, если представлены в аналитическом виде, т.е. в виде функций. Можно построить полином. Однако во многих случаях эмпирические данные по Х и по Y не являются достаточно точными (ошибки измерений, влияние других факторов, ограниченный объем массива наблюдений). Поэтому представляет интерес выбор такой аппроксимирующей функции  , чтобы значения её находились достаточно близко от известных (наблюдаемых) значений
, чтобы значения её находились достаточно близко от известных (наблюдаемых) значений  при наблюдаемых значениях
при наблюдаемых значениях  , но не обязательно совпадали с ними.
, но не обязательно совпадали с ними.
Например, по расположению эмпирической линии регрессии на рис.3.2 можно предположить, что форма корреляционной связи – линейная.
Уравнение парной линейной регрессии:
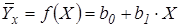 ,
,
где
 - параметры уравнения регрессии.
- параметры уравнения регрессии.
Линия регрессии, построенная по уравнению регрессии, называется теоретической линией регрессии.
Интерпретация параметров уравнения парной линейной регрессии (рис.3.2):
параметр  – это постоянная регрессии, определяющая точку пересечения регрессионной прямой с осью ординат. Например, если Y – валовые издержки, то
– это постоянная регрессии, определяющая точку пересечения регрессионной прямой с осью ординат. Например, если Y – валовые издержки, то  – это постоянные издержки. Экономическая интерпретация параметра
– это постоянные издержки. Экономическая интерпретация параметра  возможна не всегда. В общем случае
возможна не всегда. В общем случае  отражает средний эффект всех факторов, которые влияют на Y за исключением явно включенных в модель;
отражает средний эффект всех факторов, которые влияют на Y за исключением явно включенных в модель;
параметр  – это коэффициент регрессии. Отражает наклон линии регрессии, вдоль которой рассеяны данные наблюдений. Параметр
– это коэффициент регрессии. Отражает наклон линии регрессии, вдоль которой рассеяны данные наблюдений. Параметр  может быть интерпретирован как показатель, характеризующий изменение переменной Y, которое вызвано изменением значения Х на единицу, и равняется тангенсу угла наклона
может быть интерпретирован как показатель, характеризующий изменение переменной Y, которое вызвано изменением значения Х на единицу, и равняется тангенсу угла наклона 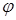 на рис.3.2.Знак параметра
на рис.3.2.Знак параметра  определяет направление этого изменения. При положительном коэффициенте регрессии с ростом значений Х растет и
определяет направление этого изменения. При положительном коэффициенте регрессии с ростом значений Х растет и 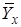 , при отрицательном – увеличение значений Х сопровождается уменьшением
, при отрицательном – увеличение значений Х сопровождается уменьшением 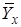 .
.
При выборе (выявлении) функциональной составляющей связи в качестве меры «близости» часто принимается квадрат расстояния между эмпирической функцией, заданной таблицей значений, и аналитическим аналогом. Такое приближение функции решается методом наименьших квадратов.
Обычный метод наименьших квадратов (МНК)
Суть метода в том, чтобы сумма квадратов отклонений расчетных значений (определенных по теоретической линии регрессии при наблюдаемых значениях  ) от наблюдаемых значений
) от наблюдаемых значений  была наименьшей.
была наименьшей.
Метод построения аппроксимирующей функции  из этого условия называется методом наименьших квадратов.
из этого условия называется методом наименьших квадратов.
В соответствии с идеей МНК необходимо минимизировать функционал
 ,
,
где
 ,
,  - значения переменных в i -том наблюдении (наблюдаемые значения);
- значения переменных в i -том наблюдении (наблюдаемые значения);
 - теоретическое (расчетное) значение Y при
- теоретическое (расчетное) значение Y при  ;
;
n - количество наблюдений.
Минимум функционала  достигается в той точке, в которой первые частные производные от функционала Q по параметрам
достигается в той точке, в которой первые частные производные от функционала Q по параметрам  и
и  обращаются в ноль:
обращаются в ноль:
 ;
;
 .
.
В результате получаем систему нормальных линейных уравнений относительно неизвестных параметров  и
и  :
:
 ;
;
 .
.
Решив систему, получим:
- коэффициент регрессии
 ; (3.1)
; (3.1)
- постоянная регрессии (свободный член)
 , (3.2)
, (3.2)
где
 - средние значения соответственно X и Y для данного массива наблюдений.
- средние значения соответственно X и Y для данного массива наблюдений.
Если фактор Х не оказывает влияния на результат Y, то  , линия регрессии параллельна оси абсцисс и
, линия регрессии параллельна оси абсцисс и  .
.
Данные для расчета параметров уравнения регрессии (пример 3.6):
| i | X | Y | 
| 
| 
|
| 1, 0 | 1, 25 | 1, 00 | 1, 250 | 1, 5625 | |
| 1, 5 | 1, 40 | 2, 25 | 2, 100 | 1, 9600 | |
| 3, 0 | 1, 50 | 9, 00 | 4, 500 | 2, 2500 | |
| 4, 5 | 1, 75 | 20, 25 | 7, 875 | 3, 0625 | |
| 5, 0 | 2, 25 | 25, 00 | 11, 250 | 5, 0625 | |
| Σ | 15, 0 | 8, 15 | 57, 50 | 26, 975 | 13, 8975 |
| Σ /5 | 3, 0 | 1, 63 | 11, 50 | 5, 395 | 2, 7795 |
 ;
;
 .
.
Тогда оцененное уравнение парной линейной регрессии в явном виде:

Если бы между Y и X существовала чисто функциональная связь, то все наблюдаемые значения Y лежали бы на теоретической линии регрессии.
Приведение нелинейных парных регрессий к линейному виду по параметрам и по переменным (линеаризация функций)
Достаточно часто между экономическими показателями имеют место нелинейные взаимосвязи. Основной прием, с помощью которого упрощается процесс оценки параметров нелинейных взаимосвязей, – их линеаризация.
Линеаризация – это переход от нелинейной формы связи (гиперболической, показательной, степенной, логарифмической и т.п.) к линейной (по внешнему виду) форме с помощью различных преобразований, что позволяет в дальнейшем оценивать параметры обычным методом наименьших квадратов.
В частности, параметры нелинейных парных регрессий можно также оценивать по выражениям (3.1) и (3.2), произведя предварительно их приведение к линейному виду.
Пример 3.7.
Если прологарифмировать степенную зависимость  , то получим её линейную по переменным и по параметрам форму
, то получим её линейную по переменным и по параметрам форму
 .
.
Полученная зависимость линейна относительно  и может быть оценена как парная линейная регрессия.
и может быть оценена как парная линейная регрессия.
Тогда при оценивании параметров  и
и  значения переменных
значения переменных  и
и  в выражениях (3.1) и (3.2) должны быть заменены на их логарифмы. Результат же для свободного члена, вычисленный по формуле (3.2), должен быть преобразован путем нахождения его антилогарифма:
в выражениях (3.1) и (3.2) должны быть заменены на их логарифмы. Результат же для свободного члена, вычисленный по формуле (3.2), должен быть преобразован путем нахождения его антилогарифма:
 .
.
|
|