Определение квадратичной формы. Закон инерции. Приведение квадратичной формы к каноническому виду методами Лагранжа и ортогонального преобразования

Квадратичной формой называется функция переменных из числового поля (поля действительных чисел) , имеющая вид , (82)

где , , .

Матрица называется матрицей квадратичной формы .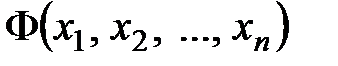

Как следует из определения квадратичной формы, - симметричная матрица, т.е. .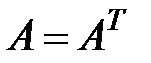

Квадратичную форму можно записать в матричном виде:

, где .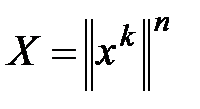

Линейным преобразованием переменных называется преобразование , , (83)

или в матричной записи 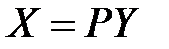, где , .

Матрица называется матрицей линейного преобразования. Справедлив закон преобразования матрицы квадратичной формы: квадратичная форма с матрицей при линейном преобразовании переменных переходит в квадратичную форму 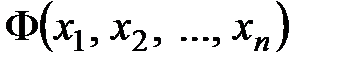с матрицей , т.е. .

Линейное преобразование (83) называется невырожденным, если его матрица - невырожденная.

В этой главе все результаты относительно квадратичной формы формулируются в классе линейных невырожденных преобразований.

Рангом квадратичной формы называется ранг ее матрицы.

Теорема 1 Ранг квадратичной формы не изменяется при линейном невырожденном преобразовании.

Теорема 2 Для любой квадратичной формы существует линейное невырожденное преобразование переменных, приводящее ее к каноническому виду, т.е. к виду , .

Отметим, что матрица квадратичной формы канонического вида является диагональной.

Эта теорема доказывается с помощью метода выделения полного квадрата, который называется методом Лагранжа. Следует иметь в виду, что канонический вид квадратичной формы, так же как и линейное невырожденное преобразование, которое приводит квадратичную форму к каноническому виду, определяются неоднозначно. Однако при этом справедлив закон инерции квадратичной формы: число слагаемых с положительными каноническими коэффициентами и число слагаемых с отрицательными каноническими коэффициентами постоянно и не зависит от линейного невырожденного преобразования, приводящего квадратичную форму к каноническому виду.

Линейное преобразование называется ортогональным, если его матрица является ортогональной.

Теорема 3 Для любой квадратичной формы 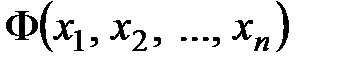с матрицей 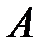существует ортогональное преобразование 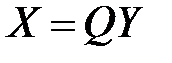, приводящее эту форму к каноническому виду , 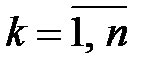. Здесь - собственные значения симметричного оператора 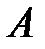, имеющего в некотором ортонормированном базисе 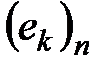евклидова пространства матрицу 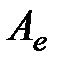, равную матрице 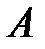, т.е. числа 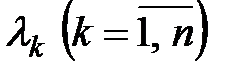являются решениями характеристического уравнения 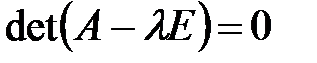. При этом если 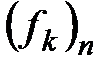- ортонормированный собственный базис оператора , то -й столбец матрицы состоит из координат элемента в базисе .

Канонические коэффициенты не зависят от выбора ортогонального преобразования.