Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вопрос №20. Преобразования Лоренца - преобразования координат и времени какого-либо события при переходе от одной инерциальной системы отсчёта к другой
|
|
Преобразования Лоренца - преобразования координат и времени какого-либо события при переходе от одной инерциальной системы отсчёта к другой. Инерциальная система отсчёта – система отсчёта, движущаяся прямолинейно с постоянной скоростью v. Преобразования Лоренца отражают равноправие всех инерциальных систем отсчёта в описании законов природы. Если инерциальная система отсчёта K' движется относительно инерциальной системы отсчёта K с постоянной скоростью v вдоль оси x, то преобразования Лоренца имеют вид
 y = y', z = z', 
| (1) |
c - скорость света в вакууме, β = v/c. Формулы, выражающие x', y', z', t' через x, y, z, t получаются из соотношения (1) заменой v на -v.
c - скорость света в вакууме, β = v/c. Формулы, выражающие x', y', z', t' через x, y, z, t получаются из соотношения (1) заменой v на -v.
При v < < c преобразования Лоренца переходят в преобразования Галилея
x = x' + vt, y = y', z = z', t = t'.
Из преобразований Лоренца следует, что промежутки времени Δ t и отрезки длины Δ l зависят от движения системы отсчёта. Если в системе K' два события, происходящие в одном и том же месте, разделены интервалом времени Δ t', то в системе K эти же происходящие в разных местах события разделены промежутком времени Δ t
Если отрезок, покоящийся в системе K', имеет длину Δ l', то его длина Δ l в системе K, т.е. расстояние между двумя одновременными в K событиями регистрации положения концов отрезка, принимает значение
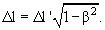
Поперечные размеры тел при этом не изменяются.
Формулы преобразования скорости:
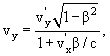
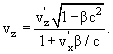
Электрическое поле E и магнитное поле H при преобразовании Лоренца преобразуются следующим образом:
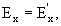
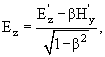
Координаты 4-мерного вектора энергии-импульса с компонентами (ε /c, px, py, pz) при преобразовании Лоренца преобразуются следующим образом:
Энергия частицы 
Импульс частицы 
Преобразования Лоренца, указывающие на относительность промежутков времени и отрезков длины между двумя событиями, оставляют инвариантной, т.е. не зависящей от выбора системы отсчёта, их комбинацию, называемую интервалом.
Инвариантом при преобразовании Лоренца является также квадрат 4-вектора энергии-импульса
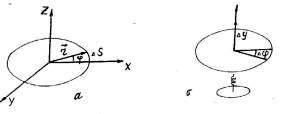Рис. 1. 5
Рассматривая угловые кинематические характеристики, отнесем их к движению частицы по окружности. Пусть частица движется по окружности в плоскости XY, вращаясь вокруг оси Z (рис. 1.5, а). Положение частицы на окружности можно задать углом Dj радиуса-вектора r с осью Х. Чтобы с помощью элементарного угла Dj определить не только изменение положения, но и направление движения частицы, введем вектор DY, которому условно припишем направление, перпендикулярное плоскости, в которой лежит дуга DS так, чтобы направление движения и направление вектора DY были связаны как вращение рукоятки буравчика (с правой нарезкой) и поступательное движение буравчика (рис. 1.5, б). Определим далее угловую скорость и угловое ускорение. Угловой скоростью называется вектор w = Dj /dt (1.17)
Численно угловая скорость w равна углу поворота радиуса-вектора материальной точки в единицу времени (или углу поворота тела в единицу времени, если речь идет о вращении тела). Вектор угловой скорости направлен перпендикулярно плоскости, в которой лежит дуга, описываемая материальной точкой, или направлена вдоль оси вращения тела (рис. 1.6 а, б).
Рис. 1.6.
Угловое ускорение (быстрота изменения угловой скорости) определяется уравнением
e = dw/dt (1.18)
Угловое ускорение можно выразить и как вторую производную угла поворота радиуса- вектора по времени. Будем обозначать угловое ускорение греческой буквой e.
Направление углового ускорения совпадает с направлением угловой скорости, если движение ускоренное и противоположно, если движение замедленное.
Угловые кинематические характеристики движения связаны с линейными достаточно простыми соотношениями. Найдем эту связь. Обратимся к рис. (1.7 а, б).
Рис.1.7.
Точка движется по окружности радиуса R. Примем центр окружности за начало отсчета. Из чертежа ясно следующее:
V = dS/dt = Rdj /dt = Rw (1.22)
Вектор v перпендикулярен плоскости, в которой лежат R и w, угол между R и w равен 90 градусам. Следовательно, можно записать векторное равенство
V = [wR] (1.23)
a=dV/dt = d(wr)/dt = [dw/dt]r + [dr/dt]w (1.24)
a = [er]+[ wV ]
Первое слагаемое в правой части (1.24) представляет собой вектор, направленный по касательной к траектории точки, движущейся по окружности, и является, следовательно, тангенциальным ускорением
at = [er] (1.25)
Второе слагаемое в (1.24) - вектор, направленный по радиусу кривизны к центру траектории. Это нормальное ускорение
an = [wV] (1.26)
Если за начало отсчета выбран центр окружности, по которой движется точка, то модули ускорений определяются как
at = eR; an = wV = w2R (1.27)
Вопрос № 9
Кинетическая энергия и ее связь с результирующей силой.
Кинетическая энергия определяется соотношением 
. Кинетическая энергия характеризует способность тела совершать механическую работу. Покажем, что это именно так. Напишем уравнение движения частицы.
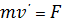Умножим обе части на ds.
Из определения скорости известно, что 
. Отсюда 
Подставим в наше выражение.
Заменяя 
, получим
Из этого выражения видно, что приращение энергии - это есть работа. Также можно заметить, что 
. Отсюда 
. Приращение кинетической энергии – это есть приращение работы и наоборот. Если проинтегрировать выражение (*), то получим
Работа результирующей всех сил, действующих на частицу, идет на приращение кинетической энергии.
Вопрос № 10
Собственная и внешняя потенциальная энергия системы материальных точек. Полная механическая энергия системы в поле внешних консервативных сил, ее связь с работой неконсервативных и сторонних сил. Закон сохранения полной механической энергии. Универсальный закон сохранения энергии.
а) Определим понятие потенциальной энергии. Пусть есть поле консервативных сил. Значение силы в каждой точке этого поля определяется некоторой функцией координат 
, которую определим следующим образом. Выберем произвольную точку О и примем значение функции в ней 
. В любой другой точке определим 
как сумму и работы 
, совершаемой силами поля при перемещении из точки В в точку О:
Поскольку работа в поле консервативных сил не зависит от пути, значения в каждой точке поля определяются однозначно.
Такая функция называется потенциальной энергией частицы во внешнем силовом поле и измеряется, как и 
, в Дж.
б) Рассмотрим взаимодействие частиц внутри системы. Возьмем простейшую систему из двух материальных точек. Силы, с которыми они взаимодействуют, будем полагать направлены вдоль прямой, соединяющей обе частицы, и зависят от расстояния между частицами.
Найдем работу внутренних сил.
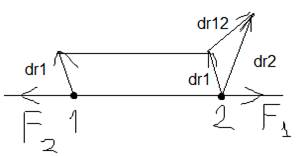dr1 – перемещение первой частицы
dr2 – перемещение второй частицы
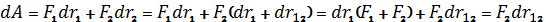Выражение 
, т.к. по третьему закону Ньютона силы, с которыми взаимодействуют два тела, равны по величины и противоположны по направлению. 
(см. рис.) говорит о том, что работу взаимодействуя двух частиц можно вычислять, считая одну из частиц неподвижной. Если опустить индексы, то получим выражение:
В случае гравитационного взаимодействия:
Для системы из N частиц, общая потенциальной энергии взаимодействия система будет равна сумме всех взаимодействий частиц взятых попарно. Например для системы из трех частиц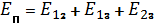 
.
Примером потенциальной энергии внутреннего взаимодействии является пружина. При ее сжатии и растяжении изменяется именно эта энергия.
в) Сумма кинетической и потенциальной энергий называется полной механической энергией частицы.
Кинетическая и потенциальная энергия могут переходить одна в другую. Однако, полная механическая энергия частицы, движущейся в поле консервативных сил, остаётся постоянной (закон сохр. полн. мех. эн.).
Работа неконсервативных сил приводит к изменению общей энергии (потенциальной энергии внутреннего взаимодействия и/или кинетической энергии и/или потенциальной энергии).
г) Универсальный закон сохранения энергии заключается в том, что полная энергия системы всегда остается постоянной. Энергия является неуничтожимой и может только переходить из одного вида в другой.
В основе закона сохранения механической энергии лежит однородность времени, т.е. равнозначность всех моментов времени в разных системах координат (время абсолютно).
Вопрос № 11
Импульс частицы - это произведение ее массы на скорость 
. Другое название этой величины - количество движения. Опыт и соответствующий анализ механических явлений показывают, что механическое движение тел характеризуется двумя величинами, которые являются основными мерами механического движения тел: первая - скалярная, вторая - векторная. Это кинетическая энергия 
и импульс частицы 
.Обе они играют центральную роль во всем построении механики.
Перейдем к более подробному рассмотрению импульса. Прежде всего, запишем основное уравнение ньютоновой динамики (3.6) в иной форме-через импульс:
| (4.1) |
т. е. производная импульса материальной точки по времени равна действующей на нее силе. В частности, если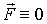 
. то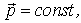 
то есть при такой записи видна четкая логическая связь между 1 и 2 законами Ньютона: первый закон утверждает, что импульс является сохраняющейся в отсутствии взаимодействия мерой движения, а второй описывает ее изменение при наличии взаимодействия.
Заметим, что в неинерциальной системе отсчета результирующая сила 
включает в себя не только силы взаимодействия данной частицы с другими телами, но и силы инерции.
Уравнение (4.1) позволяет найти приращение импульса частицы за любой промежуток времени, если известна зависимость силы от времени. Действительно, из (4.1) следует, что элементарное приращение импульса частицы за промежуток времени 
есть 
Последняя величина называется импульсом силы. Проинтегрировав это выражение по времени, найдем приращение импульса частицы за конечный промежуток времени 
:
| (4.2) |
Если сила 
то вектор 
можно вынести из-под интеграла и тогда 
. Таким образом, приращение импульса частицы за любой промежуток времени равно импульсу действующей на нее силы за то же время.
Пример. На частицу, которая в начальный момент 
имела импульс 
, действует в течение промежутка времени 
сила 
, где 
постоянный вектор. Найти, импульс частицы после окончания действия этой силы. Согласно(4.2), получим 
Перейдем к рассмотрению более сложного случая. Рассмотрим произвольную систему частиц. Введем понятие импульса системы как векторной суммы импульсов ее отдельных частиц:
| (4.3) |
где 
- импульс 
частицы. Заметим, что импульс системы 
- величина аддитивная, т. е. импульс системы равен сумме импульсов ее отдельных частей независимо от того, взаимодействуют они между собой или нет.
Найдем физическую величину, которая определяет изменение импульса системы. Для этого продифференцируем соотношение (4.3) по времени:
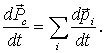
Согласно (4.1),
где 
- силы, действующие на 
частицу со стороны других частиц системы, которые обычно называют внутренние силы;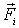 
- сила, действующая на эту же частицу со стороны других тел, не входящих в рассматриваемую систему, т.е. равнодействующая внешних сил. Подставив последнее выражение в предыдущее, получим
В этом равенстве двойная сумма справа - это сумма всех внутренних сил. В соответствии с третьим законом Ньютона силы взаимодействия между частицами системы попарно одинаковы по модулю и противоположны по направлению. Поэтому результирующая сила в каждой паре взаимодействия равна нулю, а значит, равна нулю и векторная сумма всех внутренних сил. В результате последнее уравнение принимает следующий вид:
| (4.4) |
- результирующая всех внешних сил 
.
Уравнение (4.4) означает: производная импульса системы по времени равна векторной сумме всех внешних сил, действующих на частицы системы.
Как и в случае одной частицы, из уравнения (4.4) следует, что приращение импульса системы за конечный промежуток времени есть
| (4.5) |
т. е. приращение импульса системы равно импульсу результирующей всех внешних сил за соответствующий промежуток времени. В соотношении (4.5), конечно, 
результирующая всехвнешних сил, действующих на тела системы.
Уравнения (4.4) и (4.5) справедливы как в инерциальной, так и в неинерциальной системах отсчета, если в неинерциальной системе отсчета учесть и действие сил инерции, играющих роль внешних сил, т. е. под в этих уравнениях надо понимать сумму 
, где результирующая всех внешних сил взаимодействия - это 
, а результирующая всех сил инерции обозначена 
.
Из уравнения (4.4) можно сделать важный вывод - импульс системы может изменяться под действием только внешних сил. Внутренние силы не могут изменить импульс системы независимо от их конкретного вида. Система, на которую не действуют внешние силы, называется замкнутой. Отсюда непосредственно вытекает и другой важный вывод - закон сохранения им пульса: в инерциальной системе отсчета импульс замкнутой системы частиц остается постоянным, т. е. не меняется со временем:
| (4.6) |
При этом импульсы отдельных частиц или частей замкнутой системы могут меняться со временем, что и подчеркнуто в последнем выражении. Однако эти изменения всегда происходят так, что приращение импульса одной части системы равно убыли импульса оставшейся части системы. Другими словами, отдельные части замкнутой системы могут только обмениваться импульсами. Обнаружив в некоторой системе приращение импульса, можно утверждать, что это. приращение произошло за счет убыли импульса в окружающих телах.
В этом смысле уравнение (4.4) и. (4.5) следует рассматривать как более общую формулировку закона изменения импульса, формулировку, в которой указана причина изменения импульса у незамкнутой системы - действие других тел, то есть внешних сил. Сказанное справедливо, разумеется, только по отношению к инерциальным системам отсчета.
Импульс может сохраняться и у незамкнутой системы при условии, что результирующая всех внешних сил равна нулю. Это непосредственно вытекает из уравнений (4.4) и (4.5). В практическом отношении сохранение импульса в этих случаях представляет особый интерес, ибо дает возможность получать достаточно простым путем ряд заключений о поведении системы, не вникая в детальное рассмотрение процесса.
Кроме того, у незамкнутой системы может сохраняться не сам импульс , а его проекция 
на некоторое направление 
. Это бывает тогда, когда проекция результирующей внешней силы на направление равна нулю, т. е. вектор перпендикулярен ему. Действительно, спроектировав уравнение (4.4), получим
| (4.7) |
откуда следует, что если 
, то 
. Например, при движении системы в однородном поле сил тяжести сохраняется проекция ее импульса на любое горизонтальное направление, при любых внутренних процессах в системе.
Зако́ н сохране́ ния и́ мпульса (Зако́ н сохране́ ния количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц)замкнутой системы есть величина постоянная.
В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.
Как и любой из фундаментальных законов сохранения, закон сохранения импульса описывает одну из фундаментальных симметрий, — однородность пространства.
Рассмотрим второй закон Ньютона
Перепишем его для системы из N частиц:
где суммирование идет по всем силам, действующим на n-ю частицу со стороны m-ой. Согласно третьему закону Ньютона, силы вида 
и 
будут равны по абсолютному значению и противоположны по направлению, то есть 
Тогда после подстановки полученного результата в выражение (1) правая часть будет равна нулю, то есть:
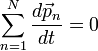
или
Как известно, если производная от некоторого выражения равна нулю, то это выражение есть постоянная величина относительно переменной дифференцирования, а значит:
(постоянный вектор).
То есть суммарный импульс системы частиц есть величина постоянная. Нетрудно получить аналогичное выражение для одной частицы.
Следует учесть, что вышеприведенные рассуждения справедливы лишь для замкнутой системы.
Также стоит подчеркнуть, что изменение импульса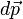 
зависит не только от действующей на тело силы, но и от продолжительности её действия.
|
|