Способ 5

Критерий Z_о является минимальным (максимальным) из частных критериев z_i (частные критерии должны быть одной размерности и вида экстремума)

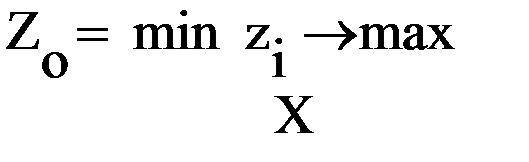или

.

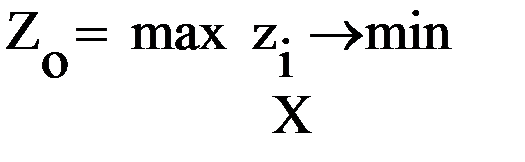Для придания гибкости этому способу можно использовать весовые коэффициенты k_i при z_i. Изменяя набор k_i, можно определять необходимые цели.

Способ 6

Критерий Z_о является одним из множества частных критериев z_i (главным), отвечающим основной цели. По остальным критериям может проверяться выполнение наложенных на них ограничений.

10.Общая схема исследования распределения случайных величин

Укрупненный алгоритм программы для исследования случайных величин приведен на рисунке 2.12.

1

Пуск

Ввод n, x_i, 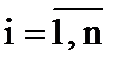n – размер выборки

x_i – числа выборки

x_с, закон распре- x_c – величина сдвига

деления

N, X_min, X_max, x_м, s², V, соответственно число интервалов,

X_j, X_сj, M_j, p_эj и др. минимальные и максимальные чис-

ла выборки, матожидание, дисперсия,

5 коэффициент вариации, границы и сере-

Параметры теоре- дины интервалов, частоты и частости

ческого распреде-

ления, F_j , p_j, ста- F_j – функция распределения

тистики критериев p_j – теоретическая вероятность

Вывод парамет-

ров распределе-

ния, статистик кри-

териев, графиков

Да 7

Продолжить

расчеты?

Нет

Останов

11.Оценивание параметров теоретического закона распределения

Значимость факторов оценивается по критерию Стьюдента.

Статистика критерия Стьюдента t_j рассчитывается по формуле

t _j = abs(b _j / s _bj),

где b_j – значение параметра (коэффициента) при факторе x_j в уравнении регрессии;

s _bj – среднеквадратическое отклонение параметра b _j.

Если расчетное значение статистики критерия Стьюдента t_j для выборочного параметра (коэффициента) при рассматриваемом факторе больше табличного значения критерия t_{т γ, k}, то считается, что нет оснований считать данный фактор малозначимым. Табличное значение t_{т γ, k} определяется заданной доверительной вероятностью γ и числом степеней свободы k. Число степеней свободы определяется по выражению

k = m - n - 1,

где m – число эмпирических точек, в которых определен зависимый показатель; n – число факторов, входящих в регрессионное уравнение.

Доверительный уровень значимости рекомендуется принимать равным 0.01–0.1 (чем меньше γ, тем выше требования к достоверности модели).

Для проверки существенности коэффициента множественной корреляции и таким образом согласованности уравнения регрессии с экспериментальными данными используется статистика критерия Фишера

или

,

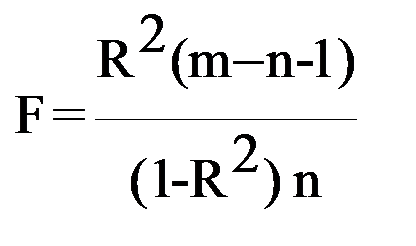где 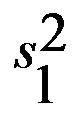и 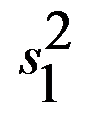– соответственно объясненная и остаточная дисперсия для зависимого параметра.

Чтобы не было оснований отвергнуть гипотезу, что экспериментальные данные согласуются с полученным уравнением регрессии, рассчитанная статистика критерия Фишера должна быть больше табличного значения (F > F_т). Табличное значение F_т определяется в зависимости от уровня значимости и числа степеней свободы k₁ и k₂:

k₁ = n;

k₂= m - n- 1.

Уровень значимости (вероятность) рекомендуется принимать 0.01 – 0.05 (чем меньше, тем жестче требования к адекватности модели).

Если F < F_т, то считается, что уравнение регрессии не согласуется с экспериментальными данными.

Статистику критерия Фишера можно использовать для оценки значимости отдельных факторов. Фактор является малозначимым в том случае, если его исключение из модели не вызывает существенного снижения статистики критерия Фишера. При этом исключение малозначимого фактора может обеспечить увеличение статистики F. Например, если при m = 7 и n = 3 имели 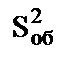=2.1, а 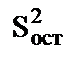=0.7, а при исключении одного из факторов (n=2) получили 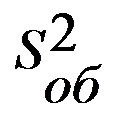=1.8 и 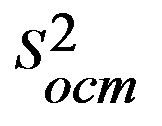=1.0, то

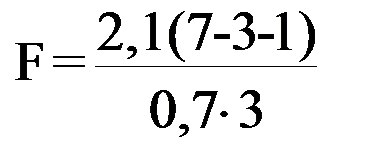=3.0 при n=3;

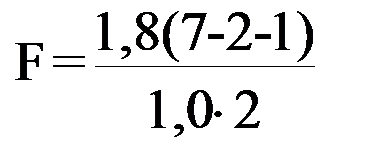=3, 6 при n=2

Увеличение статистики F в приведенном примере указывает на малозначимость исключаемого из модели фактора.

Мерой согласованности уравнения регрессии с экспериментальными данными может служить также коэффициент средней линейной ошибки аппроксимации E

.

Компьютерная программа проведения множественного корреляционно-регресионного анализа приведена в приложении 4.

12.Постановка задач принятия решений и разработка моделей

При решении задач организации производственных процессов и управления ими используются методы математического моделирования и оптимизации на основе системного подхода. Принятие решений основывается на формализованном описании задачи, количественном анализе влияющих факторов и достигаемых целей. Решение получают на основе применения методов оптимизации. Ряд методов объединяется под названием " исследование операций". При транспортной деятельности решения могут приниматься также на основе транспортной логистики.

Принятие решений включает разработку математической модели задачи, исследование модели и нахождение оптимального решения, анализ и синтез полученных результатов.

Оптимальное – это такое решение, которое обеспечивает экстремум (максимум, минимум) целевой функции (критерия оптимальности) при выполнении заданной системы ограничений.

Критерии оптимальности должны быть представительными, чувствительными к изменениям оптимизируемых параметров и как можно более простыми. Цель может быть правильно сформулирована только с позиций надсистемы.

Под системой понимается множество подсистем (объектов, подразделений), которые функционируют как единое целое по выполнению поставленной цели.

Системный подход предполагает учет всех факторов, влияющих на решение задачи, в том числе и взаимодействие с внешней средой. Он состоит в том, что, опираясь на понимание функционирования системы как единого целого, исследуются внутренние связи между отдельными элементами и внешние связи с другими системами и объектами.

Модели служат отображениями (прообразами) реальных систем, процессов, явлений; могут быть физические и математические. Математические модели представляют собой описание задачи в виде совокупности соотношений (уравнений, неравенств, логических условий), определяющих связи между параметрами функционирования исследуемой системы, ограничения и критерий оптимальности.

Модель должна быть как можно более адекватна оригиналу. Понятие адекватности модели связано с такими общими кибернетическими терминами как " черный ящик", изоморфизм, гомоморфизм.

" Черный ящик" – это система, в которой доступны наблюдению только внешние входные и выходные параметры, а внутреннее устройство неизвестно. Исследуется по связям между значениями входных и выходных параметров.

Системы, характеризующиеся одинаковыми наборами входных и выходных величин (одинаково реагирующие на внешние воздействия), независимо от их внутренней структуры, называются изоморфными. В силу изоморфности систем исследование " черного ящика" не может привести к однозначному выводу о внутренней структуре системы. Любая из изоморфных систем может рассматриваться как модель остальных.

Система, полученная из исходной путем упрощения, является ее гомоморфной моделью. Математическая модель, как правило, находится в гомоморфном отношении к реальному объекту. Она должна отражать связи между входными и выходными параметрами системы и является основой для вычисления значений критериев и проверки ограничений.

Если факторы, от которых зависит функционирование системы, разделить на известные A= {a₁, a₂,..., a_m}, на которые влиять нельзя, и управляемые X= {x₁, x₂,..., x_k}, учесть получаемые выходные параметры Y = {y₁, y₂,..., y_n}, заданный вектор целевой функции Z= {z₁, z₂ ,..., z_p} и ограничения O={o₁, o₂,..., o_s}, то имеем:

Y=F(A, X);

;

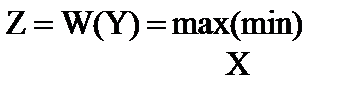O=G(А, X, Y)< > =0,

где F, Z, O – функции.

Формулировка задачи принятия решений следующая:

при заданных условиях А требуется найти такие значения элементов вектора Х, при которых вектор целевых функций Z обращается в максимум (минимум) и выполняются ограничения O.

Когда не все условия, в которых происходит функционирование системы заранее известны, то имеется еще один набор факторов U= {u₁, u₂,..., u_r}. Это переводит задачу в другую категорию – принятие решения в условиях неопределенности. Формулировка задачи следующая:

при заданных условиях А с учетом неизвестных параметров (факторов) U найти такие значения элементов вектора Х, которые дают экстремум вектора целевых функций Z при выполнении заданных ограничений O.

Ограничения, накладываемые на управляемые, неуправляемые и выходные параметры, могут быть связаны с лимитом ресурсов, обеспечением безопасности, являться следствием физических законов.

Решение поставленной задачи достигается по алгоритмам соответствующих методов оптимизации.

Анализ и синтез оптимального решения производится путем сопоставления вариантов на основе многокритериального подхода.

Для исследования математических моделей используются компьютеры. Необходимость применения последних возникает при обработке информации, использовании численных методов, методов случайного поиска и имитационного моделирования работы систем.

13.12. Построение полигона и гистограммы эмпирического распределения случайной величины.

в) Построить гистограмму или полигон эмпирического распределения

Для построения гистограммы по оси х откладывают границы интервалов значений случайной величины и для каждого из интервалов строится прямоугольник, высота которого равна частному от деления частости данного интервала на величину интервала: f_эj= p_эj/h, где f_эj – эмпирическая функция плотности вероятности. Полигон строится также по значениям f_эj, но на серединах интервалов в виде ломаной линии (рисунок 2.10).

1

0.25

f_эj

0.15

0.10 2

0.05

X_мin X_max х

X₀ X₁ X₂ X_j (j=N)

Рисунок 2.10 – Гистограмма (1) и полигон (2) эмпирического распределения (пример)

г) определить значения эмпирической функции распределения и построить ее график

(рисунок 2.11). При этом 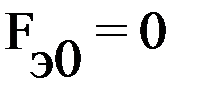(j=0).

14.Принятие гипотезы о теоретическом законе распределения

Оценка согласованности эмпирического и теоретического распределений может производиться по критериям Колмогорова, Пирсона, Романовского и Мизеса-Смирнова.

По критерию Колмогорова, Пирсона и Романовского оценка считается обоснованной при числе наблюдений не менее 100 и по критерию Мизеса-Смирнова – не менее 50. При применении критерия Колмогорова для меньшего размера выборки необходимо использовать заранее известные значения математического ожидания и среднеквадратического отклонения случайной величины, а не их выборочные оценки.

Ниже приводится порядок проверки выдвинутой гипотезы о законе распределения случайной величины по различным критериям.