
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчетные формулы
|
|
1. Модель с аддитивной сезонной составляющей
yt = f(t) + S(t) + ε t, (17.1)
где f(t) – тренд;
S(t) – сезонная составляющая;
ε t – случайная компонента.
2. Модель с мультипликативной сезонной составляющей:
yt = f(t)  S(t)
S(t)  ε t (17.2)
ε t (17.2)
3. Модель временного ряда с циклическими колебаниями периодичностью k:
yt = b0 + b1t + c1x1 + c2x2 + … + ck-1x k-1 + ε t (17.3)
| где xj = | { | 1 для j + nk, n = 0, 1, 2, … 0 для всех остальных случаев |
44. Критерий настройки параметра адаптации
Как уже неоднократно отмечалось, для проведения расчетов по адаптивным моделям необходимо задать начальные значения 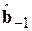 ,
,  ,
,  и определить оптимальные в некотором смысле параметры
и определить оптимальные в некотором смысле параметры  ,
, 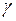 ,
,  , а для моделей с многошаговым алгоритмом адаптивного механизма и параметр
, а для моделей с многошаговым алгоритмом адаптивного механизма и параметр 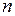 .В принципе, для достаточно длинных временных рядов выбор начальных значений может быть произвольным. С течением времени влияние начальных значений на прогнозные расчеты в результате многократного сглаживания перестает ощущаться. Однако в экономике часто приходится иметь дело с короткими временными рядами и, поэтому, от выбора начальных значений зависит точность окончательных результатов. Кроме того, при задании начальных значений мы должны учитывать то обстоятельство, что в самонастраивающейся структуре адаптивного механизма предусмотрен вариант построения адаптивной модели с постоянными коэффициентами, которые по схеме построения такого варианта полагаются равными начальным значениям. Если же выбор начальных значений осуществлять произвольным образом, например, положить все компоненты вектора
.В принципе, для достаточно длинных временных рядов выбор начальных значений может быть произвольным. С течением времени влияние начальных значений на прогнозные расчеты в результате многократного сглаживания перестает ощущаться. Однако в экономике часто приходится иметь дело с короткими временными рядами и, поэтому, от выбора начальных значений зависит точность окончательных результатов. Кроме того, при задании начальных значений мы должны учитывать то обстоятельство, что в самонастраивающейся структуре адаптивного механизма предусмотрен вариант построения адаптивной модели с постоянными коэффициентами, которые по схеме построения такого варианта полагаются равными начальным значениям. Если же выбор начальных значений осуществлять произвольным образом, например, положить все компоненты вектора  равными нулю, то, очевидно, что модель с нулевыми коэффициентами не может представлять по точности предсказания альтернативу модели с переменными коэффициентами. Следовательно, процедура, основанная на произвольном выборе начальных значений, исключает из схемы построения модели важный вариант ее возможной структуры, ухудшая в конечном итоге наследственные свойства адаптивного механизма. Поэтому, в силу приведенных здесь доводов, а также учитывая, что рассматриваемые адаптивные алгоритмы являются рекуррентными вариантами взвешенного МНК, будем для ускорения сходимости к оптимальным оценкам в качестве
равными нулю, то, очевидно, что модель с нулевыми коэффициентами не может представлять по точности предсказания альтернативу модели с переменными коэффициентами. Следовательно, процедура, основанная на произвольном выборе начальных значений, исключает из схемы построения модели важный вариант ее возможной структуры, ухудшая в конечном итоге наследственные свойства адаптивного механизма. Поэтому, в силу приведенных здесь доводов, а также учитывая, что рассматриваемые адаптивные алгоритмы являются рекуррентными вариантами взвешенного МНК, будем для ускорения сходимости к оптимальным оценкам в качестве  задавать матрицу, обратную матрице системы нормальных уравнений обычного МНК
задавать матрицу, обратную матрице системы нормальных уравнений обычного МНК  В Вкачестве
В Вкачестве 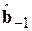 и
и  выбираются векторы коэффициентов регрессионной модели, вычисленные с помощью МНК по данным одних и тех же временных рядов
выбираются векторы коэффициентов регрессионной модели, вычисленные с помощью МНК по данным одних и тех же временных рядов  , (5.69)
, (5.69)  , (5.70)где
, (5.70)где 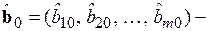 вектор-столбец оценок коэффициентов регрессионной модели;
вектор-столбец оценок коэффициентов регрессионной модели;  вектор-столбец значений зависимой переменной в момент времени
вектор-столбец значений зависимой переменной в момент времени  ;
; 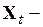 матрица значений независимых переменных из
матрица значений независимых переменных из  строк
строк 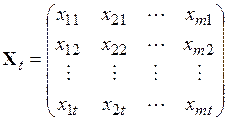 .Начальные значения, задаваемые в виде (6.68)–(6.70), позволяют в структуре возможных вариантов адаптивной модели предусмотреть регрессионную модель с постоянными коэффициентами, определяемыми по МНК, как альтернативную модели с переменными коэффициентами. Это является убедительным аргументом в пользу такого способа определения начальных значений. Кроме того, известно, что именно этот способ обеспечивает быструю сходимость к оптимальным оценкам МНК.Для определения оптимальных значений
.Начальные значения, задаваемые в виде (6.68)–(6.70), позволяют в структуре возможных вариантов адаптивной модели предусмотреть регрессионную модель с постоянными коэффициентами, определяемыми по МНК, как альтернативную модели с переменными коэффициентами. Это является убедительным аргументом в пользу такого способа определения начальных значений. Кроме того, известно, что именно этот способ обеспечивает быструю сходимость к оптимальным оценкам МНК.Для определения оптимальных значений 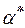 ,
,  ,
,  ,
,  проще всего применить общеизвестный метод перебора. Применение этого метода предполагает наличие критерия, с помощью которого можно из двух наборов
проще всего применить общеизвестный метод перебора. Применение этого метода предполагает наличие критерия, с помощью которого можно из двух наборов  ,
,  ,
,  ,
, 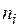 и
и  ,
,  ,
,  ,
,  различных значений параметров адаптации выбрать наилучший в некотором смысле. В принципе, критерий настройки не обязательно должен быть идентичным по своей структуре функционалу экстремальной задачи. Учитывая это замечание, критерии можно строить таким образом, чтобы они ориентировали настройку параметров адаптации на повышение определенных характеристик точности прогнозных расчетов. Рассмотрим три возможных варианта:
различных значений параметров адаптации выбрать наилучший в некотором смысле. В принципе, критерий настройки не обязательно должен быть идентичным по своей структуре функционалу экстремальной задачи. Учитывая это замечание, критерии можно строить таким образом, чтобы они ориентировали настройку параметров адаптации на повышение определенных характеристик точности прогнозных расчетов. Рассмотрим три возможных варианта:
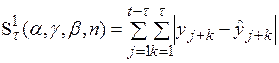

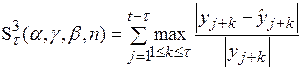 где
где 
 .
.
Первый критерий представляет собой сумму модулей ошибок прогнозирования и используется в тех случаях, когда за счет настраиваемых параметров необходимо получить минимально допустимую в рамках данной модели сумму прогнозных ошибок по всей обучающей последовательности наблюдений. Второй критерий – это сумма модулей максимальных ошибок прогнозирования. Причем, максимальная ошибка выбирается среди ошибок прогнозирования, рассчитанных для скользящего интервала длиной  . Третий критерий аналогичен второму, но только в нем суммируются относительные максимальные ошибки прогнозирования. Применение двух последних критериев следует рекомендовать в тех случаях, когда
. Третий критерий аналогичен второму, но только в нем суммируются относительные максимальные ошибки прогнозирования. Применение двух последних критериев следует рекомендовать в тех случаях, когда  и требуется, чтобы уровень ошибки предсказания построенной модели был по возможности равномерно минимальным для всего периода упреждения.Для всех трех критериев в качестве обучающей последовательности используются первые
и требуется, чтобы уровень ошибки предсказания построенной модели был по возможности равномерно минимальным для всего периода упреждения.Для всех трех критериев в качестве обучающей последовательности используются первые  наблюдений, а в качестве контрольной – группа из
наблюдений, а в качестве контрольной – группа из  последних наблюдений. Возможны и другие способы формирования обучающей и контрольной последовательности, например, деление всего выборочного множества наблюдений на две равных части – обучающую и контрольную. Настройка параметров адаптивного механизма заключается в определении оптимального набора значений
последних наблюдений. Возможны и другие способы формирования обучающей и контрольной последовательности, например, деление всего выборочного множества наблюдений на две равных части – обучающую и контрольную. Настройка параметров адаптивного механизма заключается в определении оптимального набора значений 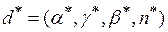 путем решения экстремальной задачи
путем решения экстремальной задачи  , (5.74)в которой в качестве целевого функционала используется любой из выше- приведенных критериев. В
, (5.74)в которой в качестве целевого функционала используется любой из выше- приведенных критериев. В 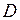 представляет собой прямое произведение множеств
представляет собой прямое произведение множеств  , где
, где  (
( – достаточно малая положительная величина),
– достаточно малая положительная величина),  ,
,  .Для решения этой задачи методом прямого перебора на множестве значений
.Для решения этой задачи методом прямого перебора на множестве значений 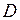 строится сетка
строится сетка
 , (5.76)
, (5.76) 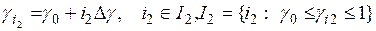 , (5.77)
, (5.77)  , (5.78)
, (5.78)  , (5.79)
, (5.79)
Для каждого узла  сетки (5.76)–(5.79) по рекуррентным формулам настраиваемого адаптивного алгоритма при заданных начальных значениях
сетки (5.76)–(5.79) по рекуррентным формулам настраиваемого адаптивного алгоритма при заданных начальных значениях  ,
, 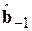 ,
,  вычисляется последовательность оценок
вычисляется последовательность оценок  , используемых в расчетах прогнозных серий
, используемых в расчетах прогнозных серий  ,
,  по
по  значений в каждой. Определенные таким образом серии прогнозных расчетов используются далее для расчета величины выбранного критерия
значений в каждой. Определенные таким образом серии прогнозных расчетов используются далее для расчета величины выбранного критерия 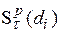 . Все полученные значения критерия (их число определяется количеством узлов сетки) сравниваются между собой, что позволяет среди узлов
. Все полученные значения критерия (их число определяется количеством узлов сетки) сравниваются между собой, что позволяет среди узлов  ,
,  (
( – множество порядковых номеров, присвоенных узлам сетки) определить такой
– множество порядковых номеров, присвоенных узлам сетки) определить такой  , для которого
, для которого  для всех
для всех  . Так определенный вектор параметров
. Так определенный вектор параметров 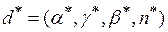 считается оптимальным. Его точность определяется задаваемым при построении сетки шагом изменения настраиваемых параметров.
считается оптимальным. Его точность определяется задаваемым при построении сетки шагом изменения настраиваемых параметров.
45. Многофакторная регрессионная модель с адаптивным механизмом
46. Дисперсионное отношение
47. Адаптивная многорегрессионная модель
48. Расстояние Махаланобиса
49. Взвешенное Евклидово расстояние. Евклидова метрика
Выбор метрики, или меры близости, является узловым моментом исследования, от которого в значительной степени зависит окончательный вариант разбиения объектов на классы при данном алгоритме разбиения. В каждом конкретном случае этот выбор должен производиться по-своему, в зависимости от целей исследования, физической и статистической природы наблюдений, априорных сведений о характере вероятностного распределения X.
Рассмотрим наиболее широко используемые в задачахкластерногоанализа расстояния и меры близости.
Обычное евклидово расстояние определяется по формуле

где xij, хkj — значения j -го признака у i -го (j -го) объекта (j= 1, 2,..., m, i, j = 1, 2,.... п).
Оно используется в следующих случаях:
а) наблюдения берутся из генеральной совокупности, имеющей многомерное нормальное распределение с ковариационной матрицей вида σ 2 Ek, где Еk — единичная матрица, т.е. исходные признаки взаимно независимы и имеют одну и ту же дисперсию;
б) исходные признаки однородны по физическому смыслу и одинаково важны для классификации.
Естественное с геометрической точки зрения евклидово пространство может оказаться бессмысленным (с точки зрения содержательной интерпретации), если признаки измерены в разных единицах. Чтобы исправить положение, прибегают к нормированию каждого признака путем деления центрированной величины на среднее квадратическое отклонение и переходят от матрицы Х к нормированнойматрице с элементами

где xil — значение l -го признака у i -го объекта;
 — среднее значение l -го признака;
— среднее значение l -го признака;
 — среднее квадратическое отклонение l -го признака.
— среднее квадратическое отклонение l -го признака.
Однако эта операция может привести к нежелательным последствиям. Если кластеры хорошо разделимы по одному признаку и не разделимы по другому, то после нормирования дискриминирующие возможности первого признака будут уменьшены в связи с усилением «шумового» эффекта второго.
Взвешенное Евклидово расстояние определяется из выражения
 (15.5)
(15.5)
где  - весовой коэффициент.
- весовой коэффициент.
Оно применяется в тех случаях, когда каждой l -й компоненте вектора наблюдений Х удается приписать некоторый «вес» ω 1, пропорциональный степени важности признака в задаче классификации. Обычно принимают 0 ≤ ω l ≤ 1, где l = 1, 2,..., k.
Определение весов, как правило, связано с дополнительными исследованиями, например с организацией опроса экспертов и обработкой их мнений. Определение весов ω l только по данным выборки может привести к ложным выводам.
50. Модели с аддитивными и мультипликативными составляющими
Временным рядом называется ряд наблюдаемых значений изучаемого показателя, расположенных в хронологическом порядке или в порядке возрастания времени.
Временные ряды могут содержать два вида компонент – систематическую и случайную составляющие.
Систематическая составляющая временного ряда является результатом воздействия постоянно действующих факторов.
Выделяют три основных систематических компоненты временного ряда:
1) тренд;
2) сезонность;
3) цикличность.
Модели, где временной ряд представлен в виде суммы перечисленных компонентов называются аддитивными, если в виде произведения – мультипликативными моделями.
Общий вид аддитивной модели следующий: Y = T + S + E. Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (T), сезонной (S) и случайной (E) компонент.
Общий вид мультипликативной модели выглядит так: Y = T * S * E. Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (T), сезонной (S) и случайной компонент (E). Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.
Построение аддитивной и мультипликативной моделей сводится к расчету значений трендовой, циклической и случайной компонент для каждого уровня ряда.
Процесс построения модели включает в себя следующие шаги:
1)Выравнивание исходного ряда методом скользящей средней.
2)Расчет значений сезонной компоненты.
3)Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных в аддитивной или мультипликативной модели.
4)Аналитическое выравнивание уровней и расчет значений тренда с использованием полученного уравнения тренда.
5)Расчет полученных по модели значений.
6)Расчет абсолютных и относительных ошибок.
Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок для анализа взаимосвязи исходного ряда и других временных рядов.
51. Логистическая кривая Перла-Рида
Логистическая кривая (кривая Перла-Рида), имеющая асимптоту, применяется, когда существует ограничение на рост показателя (уровней динамического ряда).
Логистическая кривая, или кривая Перла - Рида, - возрастающая функция, наиболее часто выражаемая в виде

другие виды этой кривой:

В этих выражениях а и b - положительные параметры; k - предельное значение функции при бесконечном возрастании времени.
Если взять производную данной функции, то можно увидеть, что скорость возрастания логистической кривой в каждый момент времени пропорциональна достигнутому уровню функции и разности между предельным значением k и достигнутым уровнем. Логарифм отношения первого прироста функции к квадрату ее значения (ординаты) есть линейная функция от времени.
Конфигурация графика логистической кривой близка графику кривой Гомперца, но в отличие от последней логистическая кривая имеет точку симметрии, совпадающую с точкой перегиба.

52. Кривая Гомпертца
Кривая Гомперца имеет аналитическое выражение:
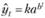
где а, b - положительные параметры, причем b меньше единицы; параметр k - асимптота функции.
В кривой Гомперца выделяются четыре участка: на первом - прирост функции незначителен, на втором - прирост увеличивается, на третьем участке прирост примерно постоянен, на четвертом - происходит замедление темпов прироста, и функция неограниченно приближается к значению k. В результате конфигурация кривой напоминает латинскую букву S.
Логарифм данной функции является экспоненциальной кривой; логарифм отношения первого прироста к самой ординате функции - линейная функция времени.
На основании кривой Гомперца описывается, например, динамика показателей уровня жизни; модификации этой кривой используются в демографии для моделирования показателей смертности и т.д.


|
|