
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Единственности решения
|
|
Рассмотрим уравнение

где  и
и 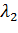 – вещественные числовые параметры, в области
– вещественные числовые параметры, в области 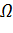 ограниченной при
ограниченной при  отрезками
отрезками 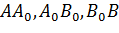 прямых
прямых  Соответственно и характеристиками
Соответственно и характеристиками 
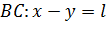 уравнения (1) при
уравнения (1) при  .
.
Задача. Найти функцию из класса

удовлетворяющую граничным условиям


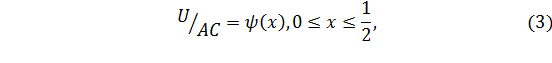
где  – заданные непрерывные функции,
– заданные непрерывные функции,  непрерывна вместе со своей производной, причем
непрерывна вместе со своей производной, причем


Введем также обозначения

Лемма 1. Если  и
и  , то любое решение уравнения (1) удовлетворяет условию
, то любое решение уравнения (1) удовлетворяет условию

При любом  .
.
Доказательство. Известно, что решение задачи Дарбу имеет вид


где 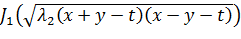 – функция Бесселя.
– функция Бесселя.
Из формулы (5) вычислим

Используя (6), преобразуем интеграл  .
.

Заменим функцию Бесселя 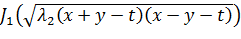 ее интегральным представлением [10]
ее интегральным представлением [10]

Тогда выражение для интеграла  примет вид
примет вид




где
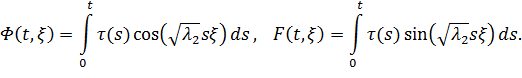
Таким образом лемма 1 доказана.
Лемма 2. Если 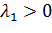 (действительное) и
(действительное) и


то для любого регулярного в области 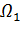 решения уравнения (1) справедливо соотношение
решения уравнения (1) справедливо соотношение

Доказательство. Пусть существует конечный предел

Тогда, переходя в уравнении (1) при  к пределу при
к пределу при  , получаем
, получаем

причем 
Из (9)  и при
и при  имеем
имеем

Интегрируя первый интеграл по частям получим





Таким образом, мы получим, что

Это и подтверждает справедливость леммы 2.
Теорема 1. Пусть  – регулярное в области решение однородной задачи, удовлетворяющее условию
– регулярное в области решение однородной задачи, удовлетворяющее условию

Тогда  в 𝛺 при всех
в 𝛺 при всех 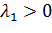 и
и 
Доказательство. Заметим, что из равенства (10) в силу лемм 1 и 2 при 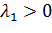
 следует, что
следует, что  на
на 
В области 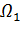 рассмотрим тождество
рассмотрим тождество

Действительно, левая часть
 равняется правой части.
равняется правой части.
Пользуясь формулой Остроградского

проинтегрируем (11) по области 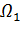 и учитывая однозначные граничные условия (8), имеем
и учитывая однозначные граничные условия (8), имеем


или


Откуда


или
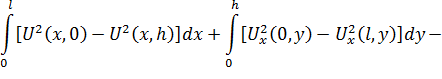

Рассмотрим


Так как по условию теоремы 1  (однородная задача).
(однородная задача).
Таким образом, получаем следующее соотношение

так как 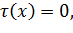 то из равенства (12) получаем, что
то из равенства (12) получаем, что 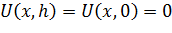 и при
и при 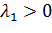

откуда следует, что  в
в 
В области  однородная задача Дарбу
однородная задача Дарбу  для уравнения (1) имеет только тривиальное решение
для уравнения (1) имеет только тривиальное решение  .
.
Следовательно,  в
в  .
.
Пусть теперь  .
.
Введем новую неизвестную функцию

или

Откуда





Подставив в уравнение (1) и сократив на  , будем иметь следующую формулу
, будем иметь следующую формулу
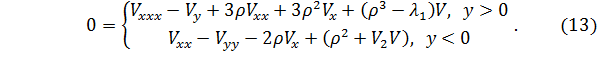
Лемма 3. Если  на
на  и
и 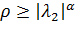 , где
, где  , то для любого регулярного в области
, то для любого регулярного в области 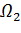 решения уравнения (13) справедливо неравенство
решения уравнения (13) справедливо неравенство

Справедливость неравенства (14) устанавливается в 
Теорема 2. Пусть  – решение однородной задачи из класса регулярных решений уравнения (1) удовлетворяющее условию
– решение однородной задачи из класса регулярных решений уравнения (1) удовлетворяющее условию
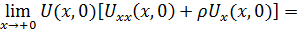
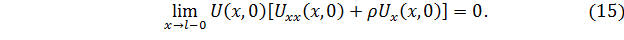
Тогда  в 𝛺, если
в 𝛺, если  , или
, или  и
и  , или
, или  .
.
Доказательство. В области  рассмотрим тождество
рассмотрим тождество



Проинтегрируем (17) по  вдоль
вдоль  , где
, где  - сколь угодно малые величины, а затем в полученном равенстве перейдем к пределу при
- сколь угодно малые величины, а затем в полученном равенстве перейдем к пределу при  и
и  .
.



Если в (15) подставить  , то (15) примет вид
, то (15) примет вид

Отсюда


Отсюда


или


Так как  , то
, то 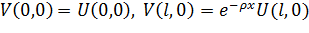 и с учетом того, что
и с учетом того, что  (однородная задача) получим, что
(однородная задача) получим, что

Далее в однородном случае краевое условие 
примет вид

Полагая в (18), будем иметь

или

Итак,


Согласно лемме 3

Тогда (19) можно записать

Для непрерывной со своими первыми производными на замкнутом интервале 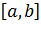 функции
функции  неравенство Фридриха
неравенство Фридриха  имеет вид
имеет вид
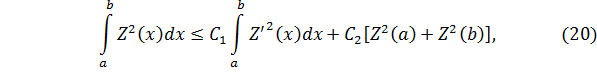
где  и
и  – постоянные. Если функция
– постоянные. Если функция  удовлетворяет дополнительным условиям
удовлетворяет дополнительным условиям  =0, то неравенство (20) примет вид
=0, то неравенство (20) примет вид
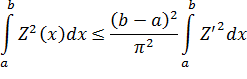
Из неравенства Фридриха имеем

и

или

Тогда, если  и
и

т.е.

то сумма двух неотрицательных слагаемых равняется нулю, это возможно только в случае, когда каждое из них равняется нулю, заключаем, что  и
и 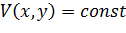 , следовательно,
, следовательно,  . Тогда из (12) имеем, что
. Тогда из (12) имеем, что  в
в 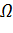 .
.
Далее рассмотрим единственность решения задачи для уравнения (1) при 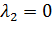 .
.
Пусть  – решение однородной задачи, для которого существует конечный предел
– решение однородной задачи, для которого существует конечный предел

Тогда переходя к пределу в уравнении (1) при  получаем функциональное соотношение между
получаем функциональное соотношение между  и
и  из параболической части
из параболической части 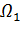 в виде (9) и в силу (8)
в виде (9) и в силу (8)
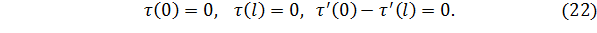
Функциональное соотношение между  и
и  из гиперболической части
из гиперболической части  на линии
на линии  имеет вид
имеет вид

Исключая  из (9) и (23), с учетом граничных условий (2) и(3) для определения функции
из (9) и (23), с учетом граничных условий (2) и(3) для определения функции  получаем следующую краевую задачу
получаем следующую краевую задачу


Характеристическое уравнение, соответствующее однородному уравнению
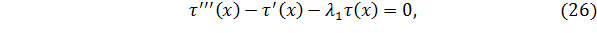
имеет вид 
Введем обозначение 
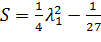 , через
, через  обозначим какое-нибудь из двух значений
обозначим какое-нибудь из двух значений  . Если
. Если  есть одно из значений корня
есть одно из значений корня  , то двумя другими значениями будут
, то двумя другими значениями будут 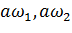 , где
, где

Аналогично, для кубического корня  обозначим его значение через
обозначим его значение через  , где
, где 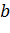 – то из значений кубического корня, для которого
– то из значений кубического корня, для которого  равно
равно  , т.е. вещественно.
, т.е. вещественно.
Рассмотрим три возможных случая

Пусть  . Тогда
. Тогда  – действительное число. В этом случае
– действительное число. В этом случае  – действительный корень,
– действительный корень,  и
и 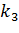 – комплексно сопряженные корни.
– комплексно сопряженные корни.
Обозначим


тогда корни уравнения (27) запишутся в виде

где 
Пусть  . Тогда
. Тогда  , где
, где  – вещественно.
– вещественно.
В рассматриваемом случае все три решения уравнения (26) вещественны, различны и имеют вид
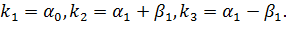
Если  . То все три решения являются вещественными, причем
. То все три решения являются вещественными, причем  если
если  и
и  при
при  . В рассматриваемом случае
. В рассматриваемом случае 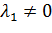 . Поэтому решения уравнения (27) имеют вид
. Поэтому решения уравнения (27) имеют вид

Решение задачи (26), (25) имеет вид



где 


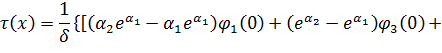
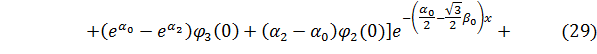

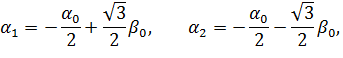
где
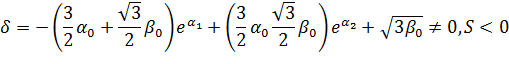


На основании (28)-(30) заключаем, что  , если выполняются условия (8).
, если выполняются условия (8).
Тогда отсюда, как показано выше, вытекает, что  в
в 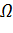 .
.
§2. Доказательство существования решения задачи 1
Пусть 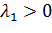 и
и  .
.
Проинтегрируем (9) от 0 до 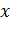 трижды
трижды
 .
.
Перепишем (9) в виде  .
.
Тогда
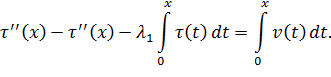
Откуда

Поменяв порядок интегрирования будем иметь
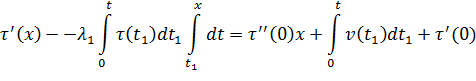
или

Откуда


или


Таким образом, получаем функциональное соотношение между  и
и 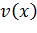 на линии
на линии  из параболической части
из параболической части  в виде
в виде


где


Если предварительно считать правую часть уравнения (31) известной и равно й  , то для
, то для  имеем интегральное уравнение типа
имеем интегральное уравнение типа

Обращая интегральное уравнение (32) получаем

где 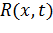 – резольвента ядра
– резольвента ядра  уравнения (32),
уравнения (32), 
Учитывая значение  из (33) получаем
из (33) получаем
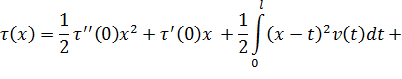

или


где
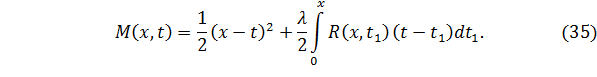
чтобы получить функциональное соотношение между  и
и  из гиперболической части
из гиперболической части  на линии
на линии  , рассмотрим решение задачи Коши
, рассмотрим решение задачи Коши  для уравнения (1) при
для уравнения (1) при  . Это решение имеет вид [5]
. Это решение имеет вид [5]


где  – функция Бесселя первого рода нулевого порядка.
– функция Бесселя первого рода нулевого порядка.
Требуя, чтобы функция, определяемая соотношением (36) удовлетворяла граничному условию (3), получаем для  интегральное уравнение типа Вольтерра
интегральное уравнение типа Вольтерра

где

Считая по формуле (37)  известной и пользуясь формулой обращения для таких уравнений [6] находим
известной и пользуясь формулой обращения для таких уравнений [6] находим

где

При получении формула (38) использовано тождество [7]

Перепишем равенство (31) с учетом значения 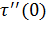 и того, что
и того, что  .
.

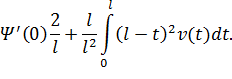
С учетом последнего (34) будем иметь вид
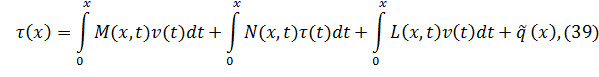
где



Исключая  из (38) и (39), получаем смешанное интегральное уравнение первого рода [8] для определения
из (38) и (39), получаем смешанное интегральное уравнение первого рода [8] для определения  :
:



где

Поскольку резольвента  в прямоугольнике
в прямоугольнике  x
x 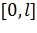 ведет себя таким же образом, как и ядро
ведет себя таким же образом, как и ядро  , то на основании свойств заданных функций
, то на основании свойств заданных функций 


 и в силу (35), (38), (40) - (43) заключаем, что функции
и в силу (35), (38), (40) - (43) заключаем, что функции 
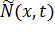 непрерывны вместе с частными производными первого порядка по переменным
непрерывны вместе с частными производными первого порядка по переменным 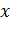 и
и  ;
; 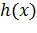 непрерывна вместе с производной, причем
непрерывна вместе с производной, причем  ,
,  .
.
Дифференцируя уравнение (43) по переменной 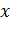 , получаем смешанное интегральное уравнение второго рода
, получаем смешанное интегральное уравнение второго рода

(44)

где
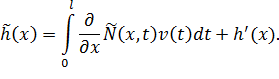
В уравнении (44) функцию  будем считать известной. Обращая его как интегральное уравнение Вольтнрра второго рода, имеем
будем считать известной. Обращая его как интегральное уравнение Вольтнрра второго рода, имеем

где 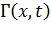 – резольвента ядра
– резольвента ядра  .
.
Заменяя теперь  его значением, получаем интегральное уравнение Фредгольма второго рода
его значением, получаем интегральное уравнение Фредгольма второго рода


где
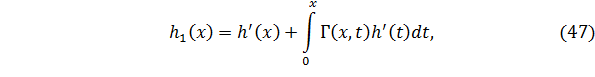
Из формулы (47) вытекает, что ядро интегрального уравнения (46)  и его правая часть
и его правая часть  непрерывны по переменным
непрерывны по переменным 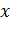 и
и  .
.
Так как эквивалентность всюду сохраняется, то из единственности решения задачи следует существования решения уравнения (46).
После нахождения функции  из (46) решения задачи в области
из (46) решения задачи в области  определяется по формуле (36), а в области
определяется по формуле (36), а в области  – как решение уравнения (1) при
– как решение уравнения (1) при  с граничными условиями (2) и условием
с граничными условиями (2) и условием  .
.
Решение этой задачи удовлетворяет интегральному уравнению

где 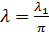


где 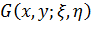 – функция Грина краевой задачи (2)
– функция Грина краевой задачи (2)  и уравнения (49), которые имеют вид[9]:
и уравнения (49), которые имеют вид[9]:
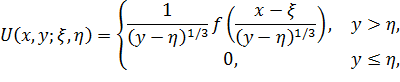
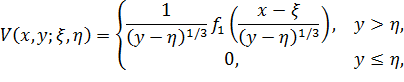
где

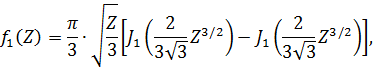
где  функция Бесселя. Функции
функция Бесселя. Функции  и
и  называются функциями Эйри и удовлетворяют уравнению
называются функциями Эйри и удовлетворяют уравнению  .
.
Основные свойства функций  и
и  , их оценки вместе с частными производными порядка
, их оценки вместе с частными производными порядка  приведены [9].
приведены [9].
К интегральному уравнению (48) применима теория Фредгольтма. Оно всегда разрешимо, так как соответствующее однородное уравнение имеет только тривиальное решение, что следует из теоремы 1 о единственности решения задачи 1.
Доказательство существования решения задачи 1, когда  , проводится аналогично предыдущему случаю.
, проводится аналогично предыдущему случаю.
Пусть теперь 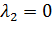 . Вид решения уравнения (24), удовлетворяющего краевым условием (25), зависит от значения величины
. Вид решения уравнения (24), удовлетворяющего краевым условием (25), зависит от значения величины  . Если
. Если  , т.е.,
, т.е.,  то решение задачи (24), (25) имеет вид:
то решение задачи (24), (25) имеет вид:


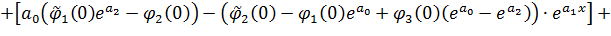


где



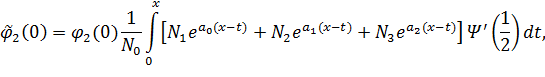

Если  , т.е.
, т.е.  , то решение задачи (24), (25) имеет вид
, то решение задачи (24), (25) имеет вид
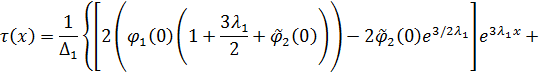


где



Аналогичным образом находится функция  в случае
в случае  , т.е.
, т.е.

или

Таким образом, после того, как функция  найдена, находим
найдена, находим  с помощью формулы (23). Следовательно, искомое решение
с помощью формулы (23). Следовательно, искомое решение  задачи в гиперболической части
задачи в гиперболической части  смешанной области находится как решение задачи Коши, а в области
смешанной области находится как решение задачи Коши, а в области  – как решение уравнения (1) при
– как решение уравнения (1) при  , удовлетворяющее граничным условиям (2) и условию
, удовлетворяющее граничным условиям (2) и условию 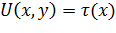 .
.
Эта задача снова эквивалентна редуцируется к интегральному уравнению Фредгольма второго рода (48), которая в силу единственности решение задачи однозначно разрешима.
|
|