Упрощение логических функций с помощью карт Карио.

Одним из способов минимизации логического выражения является использование т.н. карт Карно. Карта Карно – это графическое представление таблицы истинности. Разметка строк и столбцов карты Карно выполняется таким образом, что для любой клетки легко определить соответствующую ей комбинацию переменных по заголовкам строк и столбцов. Карта Карно позволяет упростить минимизацию функции.

Когда составляется карта Карно для заданной функции, в каждую клетку помещается, извлекаемая из строки таблицы истинности с подходящим номером: 0, если функция равняя нулю при соответствующей комбинации входных параметров, и 1 – в противном случае.

Каждая комбинация переменных с единичным значением функции в таблице истинности соответствует минтерму.

Поскольку пара соседних клеток карты Карно, содержащих единицы, указывает на наличие минтермов, различающихся значением только одной переменной, эту пару минтермов можно объединить в один терм-произведениена основании известной теоремы объединения (x y x y x). В общем случаеx так же может состоять из нескольких элементов.

Т.о. логическое выражение для вышеприведенного примера можно минимизировать следующим образом:

И окончательное минимальное выражение будет иметь вид:

36. Конечный автомат: определение, разновидности. Способы задания конечных автоматов.

Конечный автомат — абстрактный автомат, число возможных внутренних состояний которого конечное множество. Конечный автомат является математической моделью реальных дискретных устройств по переработке информации.

Конечным автоматом называется система где X; Q; Y – произвольные непустые конечные множества.

Множество называется входным алфавитом, а его элементы – входными сигналами, их последовательности – входными словами. Множество называется множество состояний автомата, а его элементы – состояниями. Множество называется выходным алфавитом, его элементы – выходными сигналами, их последовательности – выходными словами.

Функция называется функцией переходов. Функция называется функцией выходов, т.е. для

С конечным автоматом ассоциируется воображаемое устройство, которое работает следующим образом. Оно может находиться в состоянии из множества Q, воспринимать сигналы из множества Х и выдавать сигналы из множества Y.

Существует несколько эквивалентных способов задания абстрактных автоматов, среди которых можно назвать три: табличный, геометрический и функциональный.

Из определения автомата следует, что его всегда можно задать таблицей с двумя входами, содержащей m строк и n столбцов, где на пересечении столбца q и строки a стоят значения функций φ (a_i; q_j); ψ (a_i; q_j).

Другой способ задания конечного автомата – графический. При этом способе состояния автомата изображают кружками, в которой вписывают символы состояний q_j(j=1, …, n). Из каждого кружка проводится m стрелок (ориентированных ребер) взаимно-однозначно соответствующих символам входного алфавита X{a₁, …, a_m}. Стрелке, соответствующей букве a_i ϵ X и выходящей из кружка q_j ϵ Q, приписывается пара (a_i, ψ (a_i; q_j)), причем эта стрелка ведет в кружок, соответствующийφ (a_i, q_j).

Полученный рисунок называется графом автомата или, диаграммой Мура. Для не очень сложных автоматов этот способ более нагляден, чем табличный.

Третий способ задания конечного автомата А= (X; Q; Y; φ; ψ), заданного таблицей или диаграммой Мура, состоит в определении системы булевых функций.

Изложим алгоритм этого способа задания.

1. Находим числа k, r, s, удовлетворяющие условиям 2^k-1< m< 2^k; 2^r-1< n≤ 2^r; 2^s-1< p≤ 2^s, где m = |X|; n = |Q|; p = |Y|.

Очевидно, что k, r, s соответственно равны числу разрядов в двоичном представлении чиселm, n, p. Например, если m = 5, n = 17, p = 3, то k = 3, r = 5, s = 2.

2. Кодирование состояний входных и выходных символов исходного автомата.

Каждому q_j ϵ Q взаимно-однозначно ставим в соответствие двоичную последовательность длины r– двоичный код α (q) =z₁z₂…z_r. Аналогично каждому a_i ϵ X и каждому b_k ϵ Y ставим взаимно однозначно в соответствие двоичные последовательности β (α) = x₁x₂…x_k; γ (b) = y₁y₂…y_s.

Отметим, что кодирование состояний, входных и выходных символов можно провести многими способами. При этом некоторые последовательности (коды) могут оказаться неиспользованными.

Составляем следующую таблицу:

Эта таблица содержит k+r+r+s столбцов и 2^k+r строк. В первых k+r столбцах выписаны все наборы длины k+r. Каждый такой набор соответствует паре (β, α), где α – возможный код некоторого состояния, β – код входного символа.

Заполнение последних столбцов в таблице (предыдущий шаг).

Для каждой пары (a_i, q_j), гдеa_i ϵ X; q_j ϵ Q, находим β (ф)bα (q). По таблице автомата (или диаграмме Мура) определяем φ (a; q)=q^’иψ (a; q)=b. Затем находим кодα (q^’)=α ₁^’α ₂^’… α _r^’и код γ (β)=γ ₁γ ₂ …γ _s. В строку таблицы, соответствующую набору

β ₁, β ₂, …, β _k, α ₁, α ₂, …, α _r,

дописываем набор

α ₁^’, α ₂^’, …, α _r^’, γ ₁, γ ₂, …, γ _s.

Определение системы булевых функций.

После выполнения предыдущего шага может оказаться, что не все строки в таблице заполнены. Это произойдет в том случае, если хотя бы одно из чисел m, n не является степенью 2. Таким образом, функции φ ₁, φ ₂, …, φ _r, ψ ₁, ψ ₂, …ψ _s окажутся не полностью определенными – на некоторых наборах их значения не определены. Тогда мы их доопределяем произвольным образом. Как правило, до определение функций производят так, чтобы получившиеся полностью определенные функции удовлетворяли тем или иным условиям оптимальности, например представлялись минимальными ДНФ.

После выполнения этого шага исходный автомат будет задаваться системой полностью определенных булевых функций

{φ ₁, φ ₂, …, φ _r, ψ ₁, ψ ₂, …ψ _s}.

37. Автомат Мили. Структурная схема и способы задания.

Автомат Мили описывается следующими формулами:

1. внутреннее состояние автомата в следующий момент времени зависит от внутреннего состояния автомата в настоящий момент времени и входного сигнала в настоящий момент времени.

2. выходной сигнал автомата в настоящий момент времени зависит от входного сигнала в настоящий момент времени и внутреннего состояния автомата в настоящий момент времени.

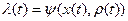
Понятие состояния автомата в момент времени t определяется внутренним состоянием автомата и состоянием входа автомата в тот же момент времени.

Автоматы, для которых функции переходов и функции выходов определены на всех парах , называются полностью определенными или полными автоматами. Соответственно, автоматы, для которых функции переходов или функции выходов определены не на всех парах , называются недоопределенными (не полностью определенными) автоматами. Состояние М(t) автомата недоопределенного на соответствующей паре , называется неиспользованным состоянием автомата. Если на каком-либо определенном состоянии автомата не определена только функция выходов, то говорят, что ему соответствует безразличное состояние выхода.

1. Таблично

2. Диаграммы Мура – граф с n вершинами

3. Функции переходов и выходов можно задать аналитически.