
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интерполяционный многочлен Лагранжа.
|
|
Пусть на интервале  задана система интерполяционных узлов
задана система интерполяционных узлов  . В которых известны значения функции
. В которых известны значения функции  . Задача интерполяции алгебраическими многочленами состоит в построении многочлена
. Задача интерполяции алгебраическими многочленами состоит в построении многочлена

степени  , значения которого в заданных узлах интерполяции совпадают со значениями функции
, значения которого в заданных узлах интерполяции совпадают со значениями функции  в этих узлах:
в этих узлах:
 . (4.1)
. (4.1)
Покажем, что поставленная задача имеет единственное решение. Для вычисления коэффициентов  ,
, 
 , составим систему линейных уравнений
, составим систему линейных уравнений
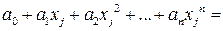
 ,
,  .
.
Определитель данной системы имеет вид:


и называется определителем Вандермонда. Такой определитель отличен от нуля, если  при
при  . В этом случае система имеет единственное решение.
. В этом случае система имеет единственное решение.
Интерполяционный многочлен естественно искать в виде

 .
.
Удовлетворяя условиям интерполяции (4.1), получаем соотношения

 ,
,
которые выполняются, если на функции  наложить ограничения
наложить ограничения
 .
.
Последние условия означают, что каждая из функций  ,
,  , имеет не менее
, имеет не менее  нулей на интервале
нулей на интервале  . Поэтому целесообразно искать эти функции в виде
. Поэтому целесообразно искать эти функции в виде
 .
.
Из условия  имеем
имеем
 .
.
Следовательно, искомые функции  вычисляются по формулам
вычисляются по формулам
 .
.
Отсюда интерполяционный многочлен имеет вид
 . (4.2)
. (4.2)
Форма представления интерполяционного многочлена в виде линейной комбинации значении приближаемой функции  с коэффициентами
с коэффициентами  называется формой Лагранжа. Если ввести обозначение
называется формой Лагранжа. Если ввести обозначение
 , (4.3)
, (4.3)
то многочлен Лагранжа можно записать в виде
 .
.
Оценка погрешности интерполяции. Погрешность приближения функции интерполяционным многочленом Лагранжа (4.2) описывается разностью
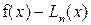 .
.
Для функций 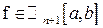 формула оценки погрешности интерполяции в точке
формула оценки погрешности интерполяции в точке  имеет вид:
имеет вид:
 , (4.4)
, (4.4)
оценка погрешности на интервале задается формулой
 (4.5)
(4.5)
Пример 4. Функция  задана своими значениями в узлах
задана своими значениями в узлах

| ||||

|
Построить интерполяционный многочлен Лагранжа. Оценить погрешность интерполяции в точке  =5, считая
=5, считая  .
.
Решение. Используя формулу (4.2), напишем интерполяционный многочлен Лагранжа

 ,
,
итак, для  получаем
получаем
 .
.
Оценим погрешность интерполяции в точке  =5, используя формулу (4.4):
=5, используя формулу (4.4):

Пример 5. Найти оценку погрешности интерполяции функции  на отрезке
на отрезке  квадратичным интерполяционным многочленом Лагранжа.
квадратичным интерполяционным многочленом Лагранжа.
Решение. По формуле (4.5) имеем
 .
.
Оценим правую часть неравенства:
 ,
,
максимальное значение

достигается в точке  :
:
 .
.
Итак, получаем следующую оценку погрешности интерполяции:

|
|