
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение модели развития экономики региона в виде векторной задачи линейного программирования
|
|
Для построения модели развития экономики региона используем агрегированную модель региона («отрасли - регион»), являющейся дальнейшим развитием модели («предприятия - отрасли - регион»), представленной впредыдущей главе. Введем понятие вектора переменных (или управляющих переменных), критериев и ограничений, накладываемых на развитие экономики региона.
Вектор переменных. В его качестве примем:
X(t)={xj(t), j=  } – вектор-столбец, каждая компонента которого определяет валовой объем выпуска продукции j-го вида деятельности в t-ом периоде (tÎ Т), показан на рис. 1, где n – множество видов деятельности на уровне разделов и подразделов, в соответствии с ОКВЭД [8], т.е. - это агрегированные виды деятельности, которые примерно соответствуют отраслям в старом понимании этого слова, Т – плановый период.
} – вектор-столбец, каждая компонента которого определяет валовой объем выпуска продукции j-го вида деятельности в t-ом периоде (tÎ Т), показан на рис. 1, где n – множество видов деятельности на уровне разделов и подразделов, в соответствии с ОКВЭД [8], т.е. - это агрегированные виды деятельности, которые примерно соответствуют отраслям в старом понимании этого слова, Т – плановый период.
Y(t)={yj(t), j=  } – вектор-столбец, каждая компонента которого определяет конечное использование (спроса) продукции j-го вида деятельности отрасли. Каждая компонента yj(t) является составной частью вектора xj(t). Для любой отрасли конечное использование yj(t) определяется суммой конечного потребления yjпот(t), накопления yjнак(t) и чистого экспорта yjэ(t): yj(t) = yjпот(t)+yjнак(t) + yjэ(t), j=
} – вектор-столбец, каждая компонента которого определяет конечное использование (спроса) продукции j-го вида деятельности отрасли. Каждая компонента yj(t) является составной частью вектора xj(t). Для любой отрасли конечное использование yj(t) определяется суммой конечного потребления yjпот(t), накопления yjнак(t) и чистого экспорта yjэ(t): yj(t) = yjпот(t)+yjнак(t) + yjэ(t), j=  .
.
I (t)={ I jин(t), j=  } – вектор-столбец, каждая компонента которого определяет валовой объем инвестиций, вкладываемых в увеличение производственных мощностей j-го вида деятельности.
} – вектор-столбец, каждая компонента которого определяет валовой объем инвестиций, вкладываемых в увеличение производственных мощностей j-го вида деятельности.
В совокупности они определяют вектор переменных:
X(t) ={X(t), I (t), Y(t)}, размерностью 3*n.
Критерии. Цель развития региона определяется постоянным увеличением благосостояния каждого жителя региона, которое зависит от роста объема выпуска каждого вида деятельности (отрасли) и соответствующих налоговых отчислений. Поэтому в качестве критерия примем максимум конечного использования каждого вида продукции:
max Y(t) = {max yj(t), j =  }.
}.
В целом по региону учитываются агрегированные показатели:
Xval(t)=  - валовой (совокупный) региональный продукт, представляющий сумму валовых выпусков продукции;
- валовой (совокупный) региональный продукт, представляющий сумму валовых выпусков продукции;
Yval(t)=  - валовое конечное использование, представляющее сумму валового конечного использования выпусков продукции всех видов деятельности
- валовое конечное использование, представляющее сумму валового конечного использования выпусков продукции всех видов деятельности
В совокупности они представляет векторный критерий оптимизации:
Opt F(X, Y)= {max Y(t), max Xval(t), max Yval(t)}. (14.1.1)
Ограничения. В модели экономики региона предусматривается три вида ограничений: балансовые, ресурсные и мощности.
Балансовые ограничения вытекают из анализа межотраслевого баланса.
Валовой объем выпуска производящей отрасли равен сумме стоимостей продукции произведенной этой отраслью и переданной (проданной) во все отрасли и конечной продукцией отрасли:
Xi(t) =  aijXj(t) + yi(t), i=
aijXj(t) + yi(t), i=  , (14.1.2)
, (14.1.2)
где Xi – валовой выпуск продукции i-ой отрасли,  aijXj(t) - промежуточное потребление, aij – коэффициенты прямых затрат, полученных от i-го вида деятельности, на производство единицы продукции j-го вида деятельности.
aijXj(t) - промежуточное потребление, aij – коэффициенты прямых затрат, полученных от i-го вида деятельности, на производство единицы продукции j-го вида деятельности.
Уравнения (14.1.2) называются балансами «выпуска».
Валовой объем выпуска потребляющей отрасли равен сумме материальных затрат на производимую продукцию в других отраслях и денежный доход от производства продукции:
Xj(t) = 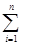 aij′ Xj(t)+zj(t), j=
aij′ Xj(t)+zj(t), j=  , (14.1.3)
, (14.1.3)
где zj(t) – денежный доход от производства продукции j-ой отрасли, включающей в себя заработанную плату z1(t), налоги z2(t), амортизацию z3(t), прибыль z4(t) и пр., т. е. zj(t)=z1j(t)+z2j(t)+z3j(t)+z4j(t), j=  - валовая добавленная стоимость j-го вида деятельности.
- валовая добавленная стоимость j-го вида деятельности.
Уравнения (14.1.3) называются балансами «затрат».
В матричном виде эти ограничения примут вид:
X(t) = AX(t) + Y(t), X(t)=A′ X(t) + Z(t), (14.1.4)
где A = {aij, i, j=  } – матрица прямых затрат.
} – матрица прямых затрат.
В совокупности балансовые уравнения (14.1.4) называются моделью Леонтьева «затраты - выпуск» [1].
Ограничения по ресурсам определяются тем, что для производства единицы продукции j-ой отрасли требуются первичные факторы (ресурсы), не являющиеся продукцией других отраслей, к которым относятся труд, земля, полезные ископаемые, финансовые ресурсы и пр.
Обозначим rij – объемом затрат i-го ресурса на производство единицы продукции j-ой отрасли:
R = {rij, j=  , i =
, i =  }.
}.
В целом ограничения примут вид:
RX(t) ≤ b(t0) + ∆ b(t0 + ∆ t), (14.1.5)
где b(t0) = {bi, i=  } – объемы i-го ресурса, имеющегося в распоряжении региона на начальный период планирования t0Î T;
} – объемы i-го ресурса, имеющегося в распоряжении региона на начальный период планирования t0Î T;
∆ b(t0+∆ t) = b(t0+∆ t)-b(t0) – вектор приращений учитываемых ресурсов в планируемом периоде (t0+∆ t), ∆ t=0, 1, 2, …, Т.
Ограничения по мощностям определяются как максимально возможные значения объемов производства X(t) по всем видам деятельности, которое лежит в пределах:
xj(t0) ≥ xj(t) ≥ xj(t0+∆ t), j=  ,
,
где xj(t0) – объемы производства (выполненных работ) j-го вида деятельности в t0 периоде, практически это отчетные данные за текущий период от (t0-1) до t0; ∆ t – планируемый период времени, как правил один год, t, (t0+∆ t)Î T; xj(t0+∆ t) – максимальные объемы производства, которые j-й вид может достичь на планируемый период времени (t0+∆ t)Î T.
Обозначим Φ j(t0) – стоимость основных фондов j-го вида деятельности в t0, Φ j(t0) представляет те инвестиции, которые вложили (с учетом выбытия) в производственные мощности j-го вида деятельности до t0. Взаимосвязь объемов производства xj(t0) со стоимостью основных фондов Φ j(t0) может быть выражена коэффициентом «фондоотдачи» [8, стр. 408]:
φ j(t0) =  , j=
, j=  .
.
Коэффициент «фондоотдачи» характеризует съем продукции в денежном выражении от одного рубля стоимости основных фондов.
Стоимость основных фондов Φ j(t0+∆ t) на период времени (t0+∆ t)Î T зависят от Φ jизн(t0+∆ t) – износа оборудования за период (t0+∆ t) и инвестиций за этот период I jин(t0+∆ t), т. е. величина инвестиций увеличивает стоимость основных фондов на свою величину (хотя и не полностью):
Φ j(t0+∆ t)= Φ j(t0)- Φ jизн(t0+∆ t)+ I jин(t0+∆ t), j=  .
.
Величина инвестиций I jин(t0+∆ t), j=  зависит от:
зависит от:
I jам (t0+∆ t) – амортизационных отчислений (инвестиций), идущих на восстановление мощностей j-го вида деятельности;
I jин(t0+∆ t) – инвестиций, вкладываемых в увеличение производственных мощностей j-го вида деятельности: инвестиции на уровне фирмы I jин.ф.(t0+∆ t), государственные ассигнования на уровне региона I jин.рег.(t0+∆ t) и государства I jин.гос.(t0+∆ t) в виде «целевых программ»:
I jин(t0+∆ t)= I jин.ф.(t0+∆ t)+ I jин.рег.(t0+∆ t)+ I jин.гос.(t0+∆ t), j=  .
.
В совокупности объемы производства на планируемый период (t0+∆ t)Î T по j-му виду деятельности равны:
xj(t0+∆ t)=xj(t0) - xjизн(t0+∆ t) + φ jkjам I jам(t0+∆ t) + φ j I jин(t0+∆ t), j=  , (14.1.6)
, (14.1.6)
где φ j – коэффициент «фондоотдачи», kjам – коэффициент использования амортизационных отчислений, j=  ;
;
xjизн(t0+∆ t)= φ j Φ jизн(t0+∆ t), Φ jизн(t0+∆ t)=kjизн Φ jот(t0).
где Φ jизн(t0+∆ t) – объем изношенных основных фондов, kjизн – коэффициент износа (выбытия) основных фондов.
В равенстве (14.1.6) величины
∆ xj(t0+∆ t) = -xjизн(t0+∆ t)+φ jkjам I jам(t0+∆ t)+φ j I jин(t0+∆ t), j=  ,
,
определяют темпы роста мощностей j=  видов деятельности в натуральных показателях (выраженных в денежных единицах), при этом, если ∆ xj(t0+∆ t)> 0, то идет обновление основных фондов, если ∆ xj(t0+∆ t)< 0, то идет устаревание основных фондов.
видов деятельности в натуральных показателях (выраженных в денежных единицах), при этом, если ∆ xj(t0+∆ t)> 0, то идет обновление основных фондов, если ∆ xj(t0+∆ t)< 0, то идет устаревание основных фондов.
Отсюда производственные мощности всех видов деятельности региона лежат в пределах xj(t0) ≤ ∆ xj(t) ≤ xj(t0)+∆ xj(t0+∆ t), j=  , или в матричном виде:
, или в матричном виде:
X(t0) ≤ X(t) ≤ X(t0+∆ t). (14.1.7)
Отношение tj = 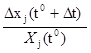 представляет показатель темпов роста (устаревания) j-го вида деятельности в относительных единицах.
представляет показатель темпов роста (устаревания) j-го вида деятельности в относительных единицах.
Обновление основных фондов и как следствие производственных мощностей зависит от величины инвестиций и коэффициента «фондоотдачи».
Коэффициент «фондоотдачи» φ j по существу представляет вектор-столбец затрат (обозначим его φ  ), которые идут на покупку товаров и услуг - результатов n – видов деятельности, в совокупности дающих увеличение производства (мощности) j-го вида деятельности на один руб. φ
), которые идут на покупку товаров и услуг - результатов n – видов деятельности, в совокупности дающих увеличение производства (мощности) j-го вида деятельности на один руб. φ  ={φ ij, i=
={φ ij, i=  }, " jÎ n,
}, " jÎ n,  =1 или φ j =
=1 или φ j =  . В целом по всем видам деятельности φ
. В целом по всем видам деятельности φ  , j=
, j=  , представляет матрицу норм воспроизводства всех видов деятельности:
, представляет матрицу норм воспроизводства всех видов деятельности:
V ={φ  ={φ ij, i=
={φ ij, i=  }, j=
}, j=  }.
}.
Матрица норм воспроизводства V вместе с инвестиционными затратами I ин:
V I ин = {φ j(I jин(t0+∆ t) + I jам(t0+∆ t)), j=  }
}
определяет объемы производства i=  видов деятельности и соответственно затрат для j=
видов деятельности и соответственно затрат для j=  видов деятельности, направленных для увеличения мощностей j=
видов деятельности, направленных для увеличения мощностей j=  видов деятельности. В итоге уравнения межотраслевого баланса (14.1.2) примут вид:
видов деятельности. В итоге уравнения межотраслевого баланса (14.1.2) примут вид:
Xi(t+∆ t) =  aijXj(t+∆ t) +
aijXj(t+∆ t) +  φ ij I jин(t+∆ t) + yi(t+∆ t), i=
φ ij I jин(t+∆ t) + yi(t+∆ t), i=  , (14.1.8)
, (14.1.8)
или в матричном виде:
X(t+∆ t) = AX(t+∆ t)+V I (t+∆ t) +Y(t+∆ t), (14.1.9)
где V I матрица воспроизводства в регионе. Подобный подход к блоку инвестиций рассмотрен в работе [66]. Равенства (14.1.9) показывают, что все отрасли региона должны трудиться не только на промежуточное потребление AX(t+∆ t) и производство продукции конечного спроса Y(t+∆ t), что было рассмотрено раннее, но и на свое воспроизводство V I (t+∆ t).
Цель развития региональной экономики направлена улучшение благосостояния населения региона, т. е. увеличения (максимизации) продукции конечного использования (спроса - КС) всех видов деятельности региона, с учетом их воспроизводства на каждый период планирования. Эта целенаправленность можно выразить критерием (14.1.1) при условии выполнения ограничений (14.1.2)-(14.1.9), что в совокупности представляет векторную задачу линейного программирования:
Opt F(X, I, Y)= {Y(t) = {max yj(t), j =  }, (14.1.10)
}, (14.1.10)
max Yval(t)=  yj(t), (14.1.11)
yj(t), (14.1.11)
max Xval(t)=  xj(t)}, (14.1.12)
xj(t)}, (14.1.12)
при ограничениях
(I-A)X(t)-V I (t) ³ Y(t), (14.1.13)
X(t)=(1-kизн)X(t0) + φ I (t), (14.1.14)
RX(t) ≤ b(t0+∆ t) + ∆ b(t), (14.1.15)
X(t0) ≤ X(t) ≤ X(t0+∆ t), I (t0) ≤ I (t) ≤ I (t0+∆ t),
Y(t0) ≤ Y(t) ≤ Y(t0+∆ t), t0+∆ t= t0, t0+1, …, t0 +T, (14.1.16)
где (10)– векторный критерий максимизации КС видов деятельности; (14.1.11)-(14.1.12) - суммарный (валовой) конечный спрос (использование) и выпуск регионального продукта соответственно; (14.1.13) - межотраслевые балансовые ограничения с учетом инвестиций; (14.1.14) – блок воспроизводства выпуска продукции с учетом инвестиций из (14.1.6):
I (t)=φ jkjам I jам(t) + φ j I jин(t), j=  ;
;
(14.1.15) – ограничения по ресурсам; (14.1.16)- ограничения по производственным мощностям, инвестициям и КС отраслей на соответствующий планируемый период ∆ t=0, 1, …, T.
Задача (14.1.10)-(14.1.16) представляет векторную задачу линейного программирования являющейся математической моделью развития экономики региона с учетом воспроизводства на планируемый период tÎ T.
Для решения задачи (14.1.10)-(14.1.16) используется алгоритм, основанный на нормализации критериев и принципе гарантированного результата [6].
Задача (14.1.10)-(14.1.16) решается в динамике с периодом планирования, как правило, один год, ∆ t=0, 1, 2, …, T.
В результате решения получим:
1) точку оптимума:
Xo(t) ={Xo(t)={x  (t), j=
(t), j=  }, I o(t)={ I
}, I o(t)={ I  (t), j =
(t), j =  }, Yo(t)={y
}, Yo(t)={y  (t), j =
(t), j =  }}, (14.1.17)
}}, (14.1.17)
где Xo(t) - валовые выпуски, I o(t) - инвестиции для всех отраслей (видов деятельности) и Yo(t) - конечное использование региона на период планирования tÎ T;
2) конечное использование всех отраслей измеренное в относительных единицах - lj(y  (t)), j =
(t)), j =  , - такое измерение позволяет сравнивать развитие отраслей друг с другом:
, - такое измерение позволяет сравнивать развитие отраслей друг с другом:
lj(y  (t))=
(t))=  , j =
, j =  , (14.1.18)
, (14.1.18)
где f 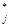 - наилучшее решение задачи (14.1.10)-(14.1.16) по j-му критерию (отрасли), f
- наилучшее решение задачи (14.1.10)-(14.1.16) по j-му критерию (отрасли), f  - наихудшее решение задачи (14.1.10)-(14.1.16) по j-му критерию;
- наихудшее решение задачи (14.1.10)-(14.1.16) по j-му критерию;
3) максимальный относительный уровень lo(t) для всех критериев lj(y  (t)), j=
(t)), j=  , он также называется гарантированным результатом в относительных единицах, который гарантирует, что все отрасли, измеренные в относительны единицах, lj(y
, он также называется гарантированным результатом в относительных единицах, который гарантирует, что все отрасли, измеренные в относительны единицах, lj(y  (t)) в точке оптимума {Xo(t), I o(t), Yo(t)} равны или больше lo(t), т.е. lj(y
(t)) в точке оптимума {Xo(t), I o(t), Yo(t)} равны или больше lo(t), т.е. lj(y  (t)) ³ lo(t), или
(t)) ³ lo(t), или
lo(t) ≤ lj(y  (t)), j =
(t)), j =  ; (14.1.19)
; (14.1.19)
т. к. критерии (виды деятельности) независимы [6], то lo(t)=lj(y 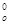 (t)), j=
(t)), j=  , для критерия (14.1.10), и lo(t) £ lk(y
, для критерия (14.1.10), и lo(t) £ lk(y  (t)), k=1, 2 для критериев (14.1.11)-(14.1.12), т. е. lo(t) является максимальным нижним уровнем для всех относительных оценок lk(X(t)), k=
(t)), k=1, 2 для критериев (14.1.11)-(14.1.12), т. е. lo(t) является максимальным нижним уровнем для всех относительных оценок lk(X(t)), k=  , а в соответствии с теоремой 2 стр. 29 [6], точка {lo, Xo, Yo} оптимальна по Парето;
, а в соответствии с теоремой 2 стр. 29 [6], точка {lo, Xo, Yo} оптимальна по Парето;
4) полученная точка оптимума Xo(t) ={Xo(t), Yo(t), I o(t)} дает возможность определить основные технико-экономические показатели региона, включенные в план, и соответствующие межотраслевые затраты:
xij(t)=  aijxi(t), " iÎ N.
aijxi(t), " iÎ N.
|
|