
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Модель рынка совершенной конкуренции
|
|
(Рассказывать в общем виде без цифр)
Построение и моделирование численной модели совершенной конкуренции покажем на основе базовой модели (5.4.6)-(5.4.10) и выполним в три этапа:
· построение численной модели совершенной конкуренции;
· решение векторной задачи, лежащей в основе модели;
· математический и графический анализ результатов решения численной модели совершенной конкуренции.
Построение численной модели совершенной конкуренции. Для совершенной конкуренции характерно то, что производственные параметры (затраты на производство продукции и стоимость продаж), как правило, у обоих производителей равны. Эти требования отразим в математической модели рынка.
Дано. Введем обозначения, уточняющие модель (5.4.6)-(5.4.10):
p 1 = p 2 = p 3 =p 4=50 - цены на продукт; a 1 = a 2 = a 3 =a 4 = 40 - затраты;
p1=p2=p3=p4 =(p 1 -a 1 )= 10 - прибыль от производства и продажи продукта;
b  =3500, b
=3500, b  =5000, l= 1, 2; bq= 5000, q= 1, 2.
=5000, l= 1, 2; bq= 5000, q= 1, 2.
Связь спроса и предложения решена следующим образом.
Спрос определяется: а) максимальной суммой, которую могут выделить потребители для своей покупки: x  +x
+x 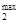 =200, где x
=200, где x  =x
=x 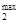 = b
= b  /p1 = b
/p1 = b 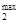 /p2 =100 единиц продукта, и ее стоимостью в pq(x
/p2 =100 единиц продукта, и ее стоимостью в pq(x  +x
+x 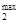 )= 10000;
)= 10000;
б) минимальной суммой, которую необходима для наименьшего потребления продукта, в x  +x
+x  = 140, где x
= 140, где x  =x
=x  = b
= b  /p1=b
/p1=b  /p2 =70 единиц продукта, и ее стоимостью в pq(x
/p2 =70 единиц продукта, и ее стоимостью в pq(x  +x
+x  )= 7000.
)= 7000.
Предложение вытекает из того, что каждая фирма может изготовить не более x  =bq/aq =125, q =1, 2 единиц товара или с учетом стоимости pqx
=bq/aq =125, q =1, 2 единиц товара или с учетом стоимости pqx  =6250. Это, с одной стороны, несколько больше, чем минимальная потребность одного потребителя, но меньше минимальной суммы потребностей обоих потребителей, т.е. 3500 =b
=6250. Это, с одной стороны, несколько больше, чем минимальная потребность одного потребителя, но меньше минимальной суммы потребностей обоих потребителей, т.е. 3500 =b 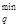 ≤ pqx
≤ pqx  ≤ pq(x
≤ pq(x  +x
+x  )= 7000,
)= 7000,
а с другой, сумма x  + x
+ x  =250 и ее стоимость pq (x
=250 и ее стоимость pq (x  + x
+ x  ) превышает максимальные потребности финансовых средств, которые могут выделить на покупку продукта от разных фирм оба потребителя.
) превышает максимальные потребности финансовых средств, которые могут выделить на покупку продукта от разных фирм оба потребителя.
Следовательно, в модели (5.4.6)-(5.4.10) с предлагаемыми числовыми параметрами, предложение превышает спрос, хотя модель может быть использована и при других взаимоотношениях спроса и предложения.
Построить оптимизационную модель рынка и рассчитать объемы спроса-предложения.
Построение модели рынка. Математическая модель рынка с двумя производителями и двумя потребителями (модель 2*2) введенными параметрами представим в виде векторной задачи линейного программирования:
opt F (X) = { max f 1(X) = 10 x1 + 10 x 2, max f 2(X) = 10 x 3 + 10 x 4, (5.4.11)
min f 3(X) = 50 x1 + 50 x 3 , min f 4(X) = 50 x2+ 50 x 4}, (5.4.12)
при ограничениях
3500 ≤ 50 x1+ 50 x3 ≤ 5000, 3500 ≤ 50 x2+ 50 x4 ≤ 5000, (5.4.13)
40 x1+ 40 x 2 ≤ 5000, 40 x 3+ 40 x4 ≤ 5000, (5.4.14)
x 1, x 2, x 3, x 4 ³ 0. (5.4.15)
Для решения векторной задачи (5.4.11)-(5.4.15) используются методы, основанные на нормализации критериев и принципе гарантированного результата, представленные во третьей части.
Моделирование поведения всех производителей и потребителей с учетом их целенаправленности выполним с помощью решения векторной задачи (5.4.11)-(5.4.15) в целом, т. е. с четырьмя критериями.
Решения векторной задачи (5.4.11)-(5.4.15) при равнозначных критерияхпредставим в виде последовательности шагов.
Шаг 1, 2. Решается задача (5.4.11)-(5.4.15) по каждому критерию отдельно.
Критерий 1. max: X  = { x 1 = 62.5, x 2=62.5, x 3=37.5, x 4=37.5},
= { x 1 = 62.5, x 2=62.5, x 3=37.5, x 4=37.5},
f 1(X  )=1250, f 2(X
)=1250, f 2(X  )=750, f 3(X
)=750, f 3(X  )=5000, f 4(X
)=5000, f 4(X  )=5000,
)=5000,
min: X 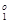 ={ x 1= 7.5, x 2= 7.5, x 3= 62.5, x 4=62.5},
={ x 1= 7.5, x 2= 7.5, x 3= 62.5, x 4=62.5},
f 1(X 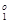 )=150, f 2(X
)=150, f 2(X 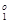 )=1250, f 3(X
)=1250, f 3(X 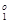 )=3500, f 4(X
)=3500, f 4(X 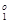 )=3500.
)=3500.
Критерий 2. max: X  ={ x 1=37.5, x 2= 37.5, x 3= 62.5, x 4= 62.5},
={ x 1=37.5, x 2= 37.5, x 3= 62.5, x 4= 62.5},
f 1(X  )=750, f 2(X
)=750, f 2(X  )=1250, f 3(X
)=1250, f 3(X  )=5000, f 4(X
)=5000, f 4(X  )=5000,
)=5000,
min: X 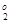 ={ x 1= 62.5, x 2=62.5, x 3= 7.5, x 4= 7.5},
={ x 1= 62.5, x 2=62.5, x 3= 7.5, x 4= 7.5},
f 1(X 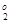 )=1250, f 2(X
)=1250, f 2(X 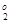 )=150, f 3(X
)=150, f 3(X 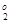 )=3500, f 4(X
)=3500, f 4(X 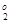 )=3500.
)=3500.
Критерий 3. min: X  ={ x 1=35.0, x 2=50.0, x 3=35.0, x 4= 50.0},
={ x 1=35.0, x 2=50.0, x 3=35.0, x 4= 50.0},
f 1(X  )=850, f 2(X
)=850, f 2(X  )=850, f 3(X
)=850, f 3(X  )=3500, f 4(X
)=3500, f 4(X  )=5000,
)=5000,
max: X  ={ x 1=50.0, x 2=50.0, x 3=50.0, x 4= 50.0}.
={ x 1=50.0, x 2=50.0, x 3=50.0, x 4= 50.0}.
f 1(X  )=1000, f 2(X
)=1000, f 2(X  )=1000, f3(X
)=1000, f3(X  )=5000, f 4(X
)=5000, f 4(X  )=5000.
)=5000.
Критерий 4. min: X  ={ x 1=50.0, x 2= 35.0, x 3=50.0, x 4= 35.0}.
={ x 1=50.0, x 2= 35.0, x 3=50.0, x 4= 35.0}.
f 1(X  )=850, f 2(X
)=850, f 2(X  )=850, f 3(X
)=850, f 3(X  )=5000, f 4(X
)=5000, f 4(X  )=3500,
)=3500,
max: X  ={ x 1= 50.0, x 2=50.0, x 3= 50.0, x 4= 50.0}.
={ x 1= 50.0, x 2=50.0, x 3= 50.0, x 4= 50.0}.
f 1(X  )=1000, f 2(X
)=1000, f 2(X  )=1000, f 3(X
)=1000, f 3(X  )=5000, f 4(X
)=5000, f 4(X  )=5000.
)=5000.
Экономическая сущность решения векторной задачи (5.4.11)-(5.4.15) на первом шаге состоит в том, что каждому участнику рынка предоставляются наиболее благоприятные условия, т. е. при расчете учитываются только их ограничения и определяются их оптимальные возможности. В результате решения получим оптимальные решения f  = fk (X
= fk (X  ), k =
), k =  - цели, к которым стремится каждый участник рынка, K =4.
- цели, к которым стремится каждый участник рынка, K =4.
Результат - оптимальные объемы продукции, которые в принципе может выпустить первый и второй производитель, и купить первый и второй потребитель.
Шаг 3. Выполняется стандартная нормализация критериев:
Анализ результатов решения, полученных по каждому критерию, выполним на основе нормализации:
l k (X  )=(fk (X
)=(fk (X  )- f
)- f  )/(f
)/(f  - f
- f  ), q, k =1, 2, 3, 4.
), q, k =1, 2, 3, 4.
l1(X  )=1.0, l2(X
)=1.0, l2(X  )=0.545, l3(X
)=0.545, l3(X  )=0.0, l4(X
)=0.0, l4(X  )=0.0,
)=0.0,
l1(X  )=0.545, l2(X
)=0.545, l2(X  )=1.0, l3(X
)=1.0, l3(X  )=0.0, l4(X
)=0.0, l4(X  )=0.0,
)=0.0,
l1(X  )=0.632, l2(X
)=0.632, l2(X  )=0.632, l3(X
)=0.632, l3(X  )=1.0, l4(X
)=1.0, l4(X  )=0.0,
)=0.0,
l1(X  )=0.632, l2(X
)=0.632, l2(X  )=0.632, l3(X
)=0.632, l3(X  )=0.0, l4(X
)=0.0, l4(X  )=1.0.
)=1.0.
Экономическая сущность решения векторной задачи (5.4.11)-(5.4.15) на втором шаге состоит в том, что цели каждого участника рынка по числовой величине выравниваются. В результате решения получаем нормализованные цели
l  = l k (X
= l k (X  ) = 1 (100%), " k Î К,
) = 1 (100%), " k Î К,
к которым стремится каждый участник рынка.
Шаг 4. Построение и решение l-задачи:
l o = max l, (5.4.16)
при ограничениях
l - (p1 x 1+ p2x2 - f 1(X 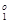 ))/(f 1(X
))/(f 1(X  )- f 1(X
)- f 1(X 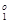 )) £ 0, (5.4.17)
)) £ 0, (5.4.17)
l - (p3 x 3 + p4 x 4 - f 2(X 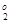 ))/(f 2(X
))/(f 2(X  ) -f 2(X
) -f 2(X 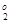 )) £ 0,
)) £ 0,
l - (p 1 x 1 + p 3 x 3- f 3(X  ))/(f 3(X
))/(f 3(X  )- f 3(X
)- f 3(X  )) £ 0,
)) £ 0,
l - (p 2 x 2 + p 4 x 4 - f 4(X  ))/(f 4(X
))/(f 4(X  ) -f 4(X
) -f 4(X  )) £ 0, (5.4.18)
)) £ 0, (5.4.18)
3500 ≤ p 1 x 1 + p 3 x 3 ≤ 5000, 3500 ≤ p 2 x 2 + p 4 x 4 ≤ 5000, (5.4.19)
a 1 x 1 + a 2 x 2 ≤ 5000, a 3 x 3 + a 4 x 4 ≤ 5000, x 1, x 2, x 3, x 4 ³ 0. (5.4.20)
Экономическая сущность решения l-задачи (5.4.16)-(5.4.20) состоит в том, что l-задача устремляет критерии (относительные оценки) всех четырех участников рынка к своему оптимуму l 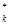 = 1, k=
= 1, k=  .
.
Решение l-задачи (5.4.16)-(5.4.20).
Результат решения при равнозначных критериях:
l o = 0.60714. Xo ={ x 1= 40.893, x 2= 40.893, x 3= 40.893, x 4= 40.893}.
f 1(Xo) = 163.572, f 2(Xo) =163.572, f 3(Xo) = 817.858, f 4(Xo) = 817.858,
l1(Xo)=0.60714, l2(Xo)=0.60714, l3(Xo)=0.60714, l4(Xo) =0.60714.
Выполняются условия l o ≤ l q (Xo), q= 1, 2, 3, 4, а в соответствии с теоремой 2 все критерии противоречивы. Любое улучшение (увеличение) одного из них приводит к ухудшению другого.
Конец
Математический и графический анализ модели совершенной конкуренции. Для оценки модели совершенной конкуренции введем некоторые преобразования: объем продукции, произведенной первым производителем, обозначим как X 1= x 1+ x 2, а вторым как X 2= x 3+ x 4. Отсюда ограничения (5.4.13)-(5.4.14) примут вид: 3500≤ 25 Х 1+25 Х 2≤ 5000, 3500≤ 25 Х 1+ 25 Х 2 ≤ 5000. 40 Х 1≤ 5000, 40 Х 2 ≤ 5000. Покажем их в системе Matlab на рис. 5.5.

Рис.5.5. Ограничения и точки оптимума в модели совершенной конкуренции
На рис. 5.5 представлены:
X1max, Х1min, X2max, Х2min – точки оптимума (наилучшее и наихудшее значение), полученные по первому и второму критерию соответственно;
Хо - точка оптимума, полученная при (четырех) равнозначных критериях, т. е. с учетом всех производителей и потребителей;
Xор 21, Xор 12 - точки оптимума, полученные при приоритете второго критерия над первым и первого над вторым соответственно;
Хоо - точка оптимума, полученная только при двух равнозначных критериях (т. е. с учетом только производителей);
Xоор 21, Xоор 12 - точки оптимума, полученные при приоритете второго критерия (производителя) над первым и первого над вторым соответственно.
Покажем эту область ограничений на трех мерном графике - рис. 5.6, где в качестве третьей координаты представим ось l - относительные оценки.

Рис. 5.6. Целевые функции в модели совершенной конкуренции на области ограничений
На этом рис. представим три функции (в относительных единицах), определяющие цели:
во-первых, индивидуальных производителей:
l1(X) =  , l2(X) =
, l2(X) =  ,
,
где f 1(X)=10 Х 1, f 2(X)=10 Х 2- текущее значение 1, 2-го критерия в допустимых точках, т. е. " X Î S; f  =1250 - величина k-го критерия в точке оптимума X
=1250 - величина k-го критерия в точке оптимума X  , k =1, 2; f
, k =1, 2; f  =150 - наихудшая величина k-го критерия в точке X
=150 - наихудшая величина k-го критерия в точке X  , k =1, 2;
, k =1, 2;
во-вторых, потребителей:
l3(X) =  ,
,
где f 3(X)=25 Х 1+25 Х 2 - текущее значение 3-го критерия в точках " X Î S; f  =3500 - величина k -го критерия в точке оптимума X
=3500 - величина k -го критерия в точке оптимума X  , k =3; f
, k =3; f  =5000 - наихудшая величина k -го критерия в точке X
=5000 - наихудшая величина k -го критерия в точке X  , k =3;
, k =3;
На рис. 5.6 область ограничений, как и на рис. 5.5, представлена точками X 1 maxX 2 minX 1 minX 2 max, образующих четырехугольник, который искусственно опущен до l= -3, (чтобы был виден). На нем также показаны точки Xo и Xo o.
Точка оптимума Xo отражает целенаправленность производителей и потребителей продукции (в виде соответствующих функций) в совокупности. Она является седловой, в ней:
· во-первых, критерии равнозначны l o =l1(Xo)=l2(Xo)= l3(Xo)=l4(Xo)= 0.607, т. е. в этой точке интересы (критерии) как производителей, так и потребителей учтены в равной мере;
· во-вторых, это равенство максимальное, т. е. не существует другой точки, в которой бы увеличение одного критерия не приводило бы к уменьшению другого, причем такая точка, только одна;
· в третьих, в терминах стоимостей финансовые затраты производителей и потребителей также равны между собой:
f å q (X)= 
 (p q + aql) xql = f å l(X)=
(p q + aql) xql = f å l(X)= 
 pqxql,
pqxql,
т. е. агрегированный спрос равен агрегированному предложению.
Точка Xoo учитывает целенаправленность только производителей продукции, деятельность которых в относительных единицах представлена кривыми l1(X) и l2(X). На рис. 5.5 эти кривые проходят через точки: X 2 max - Xоор 21- Xоо-Xоор 12- X 1 max, а на рис. 5.6 они представлены функциями (отрезками) l2 max -l o -l1 max. Эти отрезки, как указывалось ранее, представляют собой модель Курно, Штакельберга, Бертрана и Эджуорта [3, 53] и отражают конкуренцию, которая возникает во взаимоотношениях только производителей (фирм).
Точка Xoo также является седловой, в ней:
критерии равнозначны l o =l1(Xoo)=l2(Xoo)= 0.7764, т. е. в этой точке интересы (критерии) производителей учтены в равной мере;
это равенство максимальное, т. е. не существует другой точки, в которой бы увеличение одного критерия не приводило бы к уменьшению другого, причем такая точка только одна;
В терминах стоимостей финансовые затраты производителей и потребителей также равны между собой, т. е. выполняется выше приведенное равенство, но оно учитывает интересы только потребителей.
В реальной жизни необходимо учитывать не только деятельность производителей, но и их взаимоотношение с потребителями, что и показано кривыми на рис. 5.6. Эти кривые проходят через точки X 2 max - Xoр 21- Xо - Xoр 12- X 1 max, (на рис. 5.6 промежуточные точки не показаны). Эти кривые отражают конкуренцию, которая возникает во взаимоотношениях не только производителей друг с другом, но и производителей и потребителей друг с другом. И это отражается в балансе интересов производителей и потребителей, в цифровом виде это отражено равенством относительных оценок (относительно своих оптимумов).
Здесь возникает социальный аспект взаимоотношений между производителями и потребителями по вопросу распределения прибыли. Разность между относительными оценками в точках оптимума Xoo и Xo:
Dl=l(Xoo)-l(Xo)=0.7764-0.607=0.167,
показывает объем прибыли, полученный производителями, за счет интересов (целей) потребителей.
В общем, то об этих недостатках моделей подобных Курно, говорилось и раннее, но не было математического аппарата, учитывающего влияние (целенаправленность) различных фирм. И только векторная оптимизация, в которой методы решения задач построены на принципе гарантированного результата и нормализации критериев, позволила решить эту проблему.
|
|