Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Затухающие колебания.
|
|
В реальных условиях в системах, совершающих колебания, всегда присутствуют силы сопротивления. В результате система постепенно расходует свою энергию на выполнение работы против сил сопротивления и колебания, в конце концов, прекращаются.
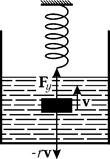 Рис. 9.1
|
Рассмотрим случай, когда колеблющееся тело находится в вязкой среде, а его скорость v невелика — рис. 9.1.
Тогда на тело действует сила сопротивления, равная
 ,
| (9.1) |
где r— коэффициент сопротивления, зависящий от формы тела и вязкости среды.
Результирующая сила, действующая на тело, равна сумме квазиупругой силы и силы сопротивления:
.
Составим уравнение движения, используя второй закон Ньютона:
.
Замечая, что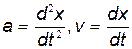 
, получим:
.
Последнее уравнение представляет собой дифференциальное уравнение затухающих колебаний, которое обычно представляют в виде:
 ,
| (9.2) |
где b=r/2m — коэффициент затухания, а 
— циклическая частота собственных свободных колебаний той же системы при b = 0.
Если пренебречь силами трения (т.е. положить b = 0), то уравнение (9.2) переходит в уравнение гармонических колебаний (5.4), решение которого имеет видx=A cos(w0t + j), где A=const.
Если же b¹ 0, но не слишком велико (т.е. 
), то зависимость, удовлетворяющая уравнению (9.2), имеет вид:
| x(t) = A(t) cos(wt + j). | (9.3) |
Здесьw — циклическая частота затухающих колебаний, которая связана с частотой незатухающих (гармонических) колебаний соотношением:
 .
| (9.4) |
Амплитуда затухающих колебаний экспоненциально убывает с течением времени:
 .
| (9.5) |
Зависимостиx(t)и A(t) показаны на рис. 9.2.
 Рис. 9.2
|
Введём некоторые характеристики затухающих колебаний.
Логарифмический декремент затухания численно равен натуральному логарифму отношения значений амплитуд затухающих колебаний в моменты времени t и t+T:
 .
| (9.6) |
Подставим (9.5) в (9.6):
 .
| (9.7) |
Логарифмический декремент затухания характеризует скорость затухания: чем больше d, тем быстрее затухают колебания.
Добротность колебательной системы определяется формулой
 .
| (9.8) |
где W(t) — энергия колебаний в момент времени t. Чем больше добротность системы, тем дольше сохраняются колебания. При малых значениях логарифмического декремента затухания справедлива формула: 
.
|
|