
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Классификация игр.
|
|
По количеству игроков – двух игроков или n игроков, если играющих больше 2. Больше отработаны для двух игроков, во многих случаях могут быть распространены на n.
По количеству стратегий – конечные и бесконечные. Если хотя бы у одного игрока бесконечное множество возможностей, то игра считается бесконечной.
По взаимоотношению сторон – кооперативные, коалиционные и бескоалиционные. Если нельзя вступать в соглашения игрокам, то бескоалиционная игра, если могут, то коалиционная игра, если коалиции известны заранее, то кооперативная.
По характеру выигрышей – с нулевой суммой (попросить вспомнить, где уже говорили об этом) и игры с ненулевой суммой, например, игры, где нужно внести первоначальный взнос за участие в игре.
По виду функции выигрышей – матричные, биматричные, непрерывные, выпуклые, сепарабельные и др. Спросить, знают ли какие-либо из перечисленных.
Биматричная -игра двух игроков с ненулевой суммой. Выигрыши каждого игрока задаются своей матрицей, размер каждой из матриц и её структура такие же как в матричной игре. Если функция выигрышей каждого игрока в зависимости от стратегий является непрерывной, то игра считается непрерывной, если выпуклая, то выпуклой. Если функция выигрышей может быть разбита на сумму произведений функций одного аргумента, то игра называется сепарабельной.
По количеству ходов – одношаговые (игра заканчивается после одного шага) и многошаговые (позиционные, стохастические, дифференциальные и др.)
По информированности сторон – с полной и неполной информацией. Если игрок на каждом ходу знает все применённые другими игроками стратегии на предыдущих ходах, то это игра с полной информацией, если не все, то с неполной.
По степени неполноты информации – статистические (в условиях частичной неопределённости) и стратегические (в условиях полной неопределённости). Игры с природой относятся к статистическим играм. Имеется возможность получения информации на основе статистического эксперимента.
Оценки стратегий матричной игры.
Если есть матрица выигрышей, состоящая из n столбцов и m строк, то это означает, что у первого игрока есть m различных стратегий, а у второго n. В каждой ячейке с номером строки i и номером столбца j записан выигрыш, который получит первый игрок, если применит стратегию с номером i, а второй при этом будет действовать в соответствии со своей j-ой стратегией. Выигрыш может быть и отрицательный, а у второго игрока выигрыш равен выигрышу первого с обратным знаком.
Подход первого игрока: он должен получить максимальный выигрыш при наихудших условиях. Игрок выбирает из каждой строки наименьшее значение (худший для себя вариант поведения второго игрока), обозначим их ai, и из этого столбца выбирает наибольшее значение, номер строки с этим значением и будет соответствовать его оптимальной стратегии ( максиминной ). Это означает, что первый игрок гарантирует себе выигрыш не меньше, чем найденное значение при любых стратегиях игрока 2. Значение a, найденное таким образом значение называется чистой нижней ценой игры.
Подход второго игрока: он должен не дать второму игроку получить большой выигрыш, то есть он стремится уменьшить выигрыш первого игрока. Второй игрок выбирает из каждого столбца максимальное значение выигрыша первого, а из полученной строки выбирает минимальное значение, номер столбца с этим значением и будет соответствовать его оптимальной стратегии ( минимаксной ). Это означает, что второй игрок гарантирует, что первый игрок не получит выигрыш больший, чем найденное значение при любой выбранной им стратегии. Значение b, найденное таким образом, называется чистой верхней ценой игры.
Чистая цена игры g - цена игры, если верхняя и нижняя цены совпадают, то есть g=a=b. В этом случае игра называется игрой с седловой точкой.
Примеры: пусть есть платёжная матрица определить для этой игры стратегии, перечисленные выше, и наличие седловой точки: 1
| Вj Ai | B1 | B2 | B3 | ai |
| A1 | ||||
| A2 | ||||
| bj |
| Вj Ai | B1 | B2 | B3 | B4 | ai |
| A1 | |||||
| A2 | |||||
| bj |
В игре с седловой точкой, если один игрок придерживается этой точки, тогда другой получит лучший результат, если тоже будет придерживаться этой точки. Оптимальные чистые стратегии – это чистые стратегии, образующие седловую точку.
В игре без седловой точки, если игрок 1 осведомлён о том, что игрок 2 будет придерживаться минимаксной стратегии, то он может выбрать оптимальную стратегию, которая не совпадает с максиминной. Пример: А=
Для игрока 1 в этом случае максиминная стратегия А2, а для второго игрока минимаксная стратегия В2. В этом случае, если первый игрок знает, что второй придерживается этой стратегии, то для него оптимальной будет стратегия А1, при которой выигрыш составит 5, превышающий максиминный 4.
При многократном повторении игры в сходных условиях можно добиться гарантированного среднего выигрыша, превосходящего для игрока 1 максиминный.
В условиях полной неопределённости возможен и другой способ задания матрицы игры в виде матрицы рисков R или матрицы упущенных возможностей.
Величина риска – это размер платы за отсутствие информации о состоянии среды. Матрица рисков строится из условий задачи или из матрицы выигрышей. Риск при использовании стратегии Аi в состоянии среды Вj – это разность между выигрышем, который игрок получил бы, если бы он знал, что состояние среды Вj, и выигрышем, который игрок получит не имея этой информации.
Зная состояние среды, игрок выбирает ту стратегию, которая даёт максимальный выигрыш при этом состоянии.
Например, для матрицы выигрышей, представленной в последней таблице, матрица рисков будет выглядеть следующим образом.
| 8-3=5 | 5-5=0 | 12-8=4 | 7-6=1 | 11-11=0 |
| 8-8=0 | 5-4=1 | 12-12=0 | 7-7=0 | 11-9=2 |
Или
В условиях полной неопределённости используются и другие критерии выбора стратегий:
Критерий максимакса – используются стратегия максимизирующая максимальный выигрыш (критерий крайнего оптимизма). Пусть есть матрица выигрышей
| Вj Ai | B1 | B2 | B3 | B4 |
| A1 | ||||
| A2 | ||||
| А3 |
Для неё стратегия А1 будет наилучшей по этому критерию.
Этим критерием часто пользуются и в экономике, если ситуация безвыходная «или пан, или пропал».
Максиминный критерий Вальда – это тот же максиминный критерий, что и в стратегических играх, где противник настроен агрессивно по отношению к игроку. И решением является стратегия, при которой достигается нижняя цена игры. В нашем случае – это стратегия А2. Такая стратегия приемлема, если игрок хочет застраховать себя от неожиданных проигрышей. Выбор такой стратегии определяется отрицательным отношением игрока к риску.
Критерий минимаксного риска Сэвиджа аналогичен критерию Вальда, но игрок руководствуется не матрицей выигрышей, а матрицей рисков. Для нашей игры матрица рисков будет выглядеть следующим образом:
| Вj Ai | B1 | B2 | B3 | B4 |
| A1 | ||||
| A2 | ||||
| А3 |
Выбирается стратегия, у которой минимален максимальный риск, в нашем случае это будет стратегия А1.
Критерий пессимизма-оптимизма Гурвица. Согласно этому критерию, стратегия в матрице выигрышей выбирается в соответствии с максимальным значением Hi. Вычисленным для каждой строки в соответствии с заданным значением р – коэффициент пессимизма, заключённый в пределах от 1 до 0, по формуле
Hi=p*min(aij)+(1-p)*max(aij).
При р=0, критерий Гурвица совпадает с максимаксным критерием, а при р=1, с критерием Вальда.
Посчитаем, какую стратегию в нашей игре лучше выбрать, при р=0, 6.
Н1=0, 6*1+0, 4*9=4, 2
Н2=0, 6*3+0, 4*8=5
Н3=0, 6*2+0, 4*6=3, 6
В этом случае лучше выбрать вторую стратегию.
Критерий Гурвица можно использовать и для матрицы рисков, в этом случае выбирается минимальное значение Hi, которое рассчитывается по формуле
Hi=p* max(rij) +(1-p)* min(rij)
При выборе р=0 осуществляется выбор по критерию наименьшего из всех возможных рисков, при р=1 – по критерию минимаксного риска Сэвиджа.
Посчитать для предыдущей задачи вариант при р=0, 6. Совпадёт ли он с полученным по матрице выигрышей.
В случае, если критерий даёт несколько решений, выбор между ними может осуществляться по дополнительному критерию, например, по среднему квадратичному отклонению от среднего выигрыша. Однозначного решения нет, всё зависит от склонности к риску ЛПР.
Для примера определить стратегии по всем приведённым критериям для следующей матрицы выигрышей
| Вj Ai | B1 | B2 | B3 | B4 |
| A1 | ||||
| A2 | ||||
| А3 | ||||
| А4 |
Если стратегия фигурирует по нескольким критериям, то лучше выбрать её, как более надёжную.
Смешанные стратегии в матричных играх.
Смешанная стратегия – это полный набор применения чистых стратегий игрока при многократном повторении игры в одних и тех же условиях с заданными вероятностями. В такой ситуации можно получить выигрыши в среднем большие нижней цены игры, но меньшие верхней.
Условия применения смешанных стратегий:
· Игра без седловой точки;
· Игроки используют случайную смесь чистых стратегий с заданными вероятностями;
· Игра многократно повторяется в сходных условиях;
· При каждом из ходов ни один игрок не информирован о выборе стратегии другим игроком;
· Допускается осреднение результатов игры.
Для игрока 1 смешанная стратегия S1 задаётся матрицей
S1=  , где
, где  =1, i=1…m
=1, i=1…m
Для игрока 2 смешанная стратегия S2 задаётся матрицей
S2=  , где
, где  =1, j=1…n
=1, j=1…n
Задача в общем случае решается из соображений, что игрок 1 стремится увеличить свой средний выигрыш, а игрок 2 довести этот эффект до минимума.
Если известны все значения pi и qj, то средний выигрыш (математическое ожидание эффекта)
M(A, P, Q) = 
Пусть элементы матрицы А положительны (спросить, как этого добиться, если есть отрицательные элементы и как потом пересчитать цену выигрыша). Матрица, где каждый элемент увеличен на величину наименьшего из отрицательных, даст следующее математическое ожидание
M(A1, P, Q) =  = M(A, P, Q) +b*
= M(A, P, Q) +b*  = M(A, P, Q) +b, то есть надо найденную цену игры уменьшить на b.
= M(A, P, Q) +b, то есть надо найденную цену игры уменьшить на b.
Существует теорема, доказывающая, что в этом случае всегда существует решение для выбора оптимальных смешанных стратегий следующим образом.
После обозначения g- цены игры при оптимальных стратегиях обоих игроков, и ui=pi/g, получают задачу линейного программирования для определения стратегии первого игрока:
Z=  ®min
®min
 ³ 1 для всех j (AT*U³ en), то есть будет j неравенств
³ 1 для всех j (AT*U³ en), то есть будет j неравенств
 для всех i
для всех i
решив эту задачу, получим решение игры в смешанных стратегиях для первого игрока. g= 1/Z min, Р =UT* g
Аналогично для второго игрока получаем задачу линейного программирования g= 1/Wmax
W=  ®max
®max
 1 для всех i (A*V£ em), то есть будет j неравенств
1 для всех i (A*V£ em), то есть будет j неравенств
 для всех j
для всех j
Такие задачи удобно решать в Excel, где мы их и рассмотрим на практических занятиях.
Мажорирование стратегий.
Очень похоже на выделение множества Парето. Отбрасываются стратегии, которые заведомо невыгодны игроку. Например, в матрице выигрышей А  с позиции второго игрока его вторую стратегию можно отбросить, так как ему не выгодно её применять при любых действиях первого игрока и т.д.
с позиции второго игрока его вторую стратегию можно отбросить, так как ему не выгодно её применять при любых действиях первого игрока и т.д.
Принятие решений на основе модели «игра с природой».
В экономической ситуации стратегические игры, описанные выше не совсем адекватны: решения принимаются, как правило, один раз, а если несколько, то чаще всего в изменяющихся условиях. Платёжную матрицу или матрицу рисков, однако, всегда желательно составить, чтобы хотя бы провести мажорирование своих стратегий (исключать стратегии природы нельзя, так как она действует случайным образом), но надо учитывать, что сознательно действуете только Вы, а природа не настроена к Вам враждебно, а просто выступает как игрок, не имеющий конкретной цели и действующий случайным образом. Термин «природа» здесь условный, это просто экономическая ситуация. Далее можно использовать любые критерии в зависимости от отношения к риску ЛПР.
Выводы.
1. Игрой называется всякая конфликтная ситуация, изучаемая в теории игр и представляющая собой упрощённую модель реальной ситуации, не учитывающая несущественные для ситуации факторы. Игра ведётся по правилам, которые могут нарушаться в реальной жизни. Стороны, участвующие в конфликте, называются игроками.
2. Матрица выигрышей состоит из n столбцов и m строк - это означает, что у первого игрока есть m различных стратегий, а у второго n. В каждой ячейке с номером строки i и номером столбца j записан выигрыш, который получит первый игрок, если применит стратегию с номером i, а второй при этом будет действовать в соответствии со своей j-ой стратегией.
3. Величина риска – это размер платы за отсутствие информации о состоянии среды. Матрица рисков строится из условий задачи или из матрицы выигрышей. Риск при использовании стратегии Аi в состоянии среды Вj – это разность между выигрышем, который игрок получил бы, если бы он знал, что состояние среды Вj, и выигрышем, который игрок получит не имея этой информации.
4. Зная состояние среды, игрок выбирает ту стратегию, которая даёт максимальный выигрыш при этом состоянии.
5. Максиминной называется стратегия, которая даётмаксимальный выигрыш при наихудших условиях
6. Минимаксной называется стратегия, при которой игрок должен не дать второму игроку получить большой выигрыш.
7. Критерий максимакса – используются стратегия максимизирующая максимальный выигрыш (критерий крайнего оптимизма).
8. Максиминный критерий Вальда – это тот же максиминный критерий, что и в стратегических играх, где противник настроен агрессивно по отношению к игроку
9. Критерий минимаксного риска Сэвиджа аналогичен критерию Вальда, но игрок руководствуется не матрицей выигрышей, а матрицей рисков. Выбирается стратегия, у которой минимален максимальный риск.
10. Критерий пессимизма-оптимизма Гурвица. Согласно этому критерию, стратегия в матрице выигрышей выбирается в соответствии с максимальным значением Hi. Вычисленным для каждой строки в соответствии с заданным значением р – коэффициент пессимизма, заключённый в пределах от 1 до 0, по формуле
Hi=p*min(aij)+(1-p)*max(aij).
11. Смешанная стратегия – это полный набор применения чистых стратегий игрока при многократном повторении игры в одних и тех же условиях с заданными вероятностями.
12. Мажорирование стратегий. Отбрасываются стратегии, которые заведомо невыгодны игроку.
13. В экономической ситуации стратегические игры, описанные выше не совсем адекватны: решения принимаются, как правило, один раз, а если несколько, то чаще всего в изменяющихся условиях. Платёжную матрицу или матрицу рисков, однако, всегда желательно составить, чтобы хотя бы провести мажорирование своих стратегий. Далее можно использовать любые критерии в зависимости от отношения к риску ЛПР.
6. Принятие решений на основе теории нечётких множеств.
Теория нечетких множеств — раздел прикладной математики, посвященный методам анализа неопределенных данных, в которых описание неопределенностей реальных явлений и процессов проводится с помощью понятия о множествах, не имеющих четких границ.
Теория нечетких множеств — это расширение классической теории множеств. В классической теории множеств принадлежность элементов некоторому множеству понимается в бинарных терминах в соответствии с четким условием — элемент либо принадлежит, либо не принадлежит данному множеству. В теории нечетких множеств допускается градуированное понимание принадлежности элемента множеству; степень принадлежности элемента описывается при помощи функции принадлежности.
Переход от принадлежности элементов заданному множеству - к непринадлежности их этому множеству происходит или может происходить постепенно, не резко.
Нечеткое множество характеризуется функцией принадлежности, отображающей некоторое множество (носитель нечеткого множества) в отрезок [0; 1]. Значение функции принадлежности показывает степень принадлежности соответствующего элемента носителя рассматриваемому нечеткому множеству. Это значение меняется от 0 (полная непринадлежность) до 1 (полная принадлежность).
Понятие " нечеткое множество" введено Л.А.Заде в 1965 г. Исходный термин - fuzzy set. Другие варианты перевода на русский язык - нечеткое, расплывчатое, размытое, туманное, пушистое множество.
Теория нечетких множеств в определенном смысле сводится к теории случайных множеств и тем самым к теории вероятностей.
Теория нечетких множеств применяется в теории и практике управления системами, в экономике и финансах для решения задач в условиях неопределенности ключевых показателей. Ряд стиральных машин и фотоаппаратов сегодня оборудованы нечёткими контроллерами.
В социологии классификация и типология может проводиться по выбранным критериям, или по эмпирически обнаруженным основаниям. Это позволяет выделить теоретические и эмпирические типологии.
Основные понятия.
Под нечётким множеством  понимается совокупность
понимается совокупность
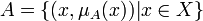 ,
,
где  — универсальное множество, а
— универсальное множество, а  — функция принадлежности (характеристическая функция), характеризующая степень принадлежности элемента
— функция принадлежности (характеристическая функция), характеризующая степень принадлежности элемента 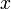 нечёткому множеству
нечёткому множеству  .Привести пример с большими рыбами, умными студентами и т.д.
.Привести пример с большими рыбами, умными студентами и т.д.
Функция  принимает значения в некотором вполне упорядоченном множестве
принимает значения в некотором вполне упорядоченном множестве  . Множество
. Множество  называют множеством принадлежностей, часто в качестве
называют множеством принадлежностей, часто в качестве  выбирается отрезок
выбирается отрезок  . Если
. Если  , то нечёткое множество может рассматриваться как обычное, чёткое множество.
, то нечёткое множество может рассматриваться как обычное, чёткое множество.
Пусть  нечёткое множество с элементами из универсального множества
нечёткое множество с элементами из универсального множества  и множеством принадлежностей
и множеством принадлежностей 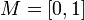 . Тогда
. Тогда
· Носителем (суппортом) нечёткого множества  называется множество
называется множество  .
.
· Величина
 называется высотой нечёткого множества
называется высотой нечёткого множества  .
.
· Нечёткое множество  нормально, если его высота равна
нормально, если его высота равна 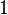 . Если высота строго меньше
. Если высота строго меньше 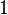 , нечёткое множество называется субнормальным.
, нечёткое множество называется субнормальным.
· Нечёткое множество пусто, если  . Непустое субнормальное нечёткое множество можно нормализовать по формуле:
. Непустое субнормальное нечёткое множество можно нормализовать по формуле:

· Нечёткое множество унимодально, если  только на одном
только на одном 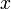 из
из  .
.
· Элементы  , для которых
, для которых 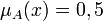 , называются точками перехода нечёткого множества
, называются точками перехода нечёткого множества  .
.
Сравнение нечётких множеств
Пусть A и B нечёткие множества, заданные на универсальном множестве X.
· A содержится в B, если для любого элемента из X функция его принадлежности множеству A будет принимать значение меньшее либо равное, чем функция принадлежности множеству B:

· В случае, если условие  выполняется не для всех
выполняется не для всех  , говорят о степени включения нечёткого множества A в B, которое определяется так:
, говорят о степени включения нечёткого множества A в B, которое определяется так:

где

· Два множества называются равными, если они содержатся друг в друге:

· В случае, если значения функций принадлежности  и
и  почти равны между собой, говорят о степени равенства нечётких множеств A и B, например, в виде
почти равны между собой, говорят о степени равенства нечётких множеств A и B, например, в виде

где 
Пример описания неопределенности с помощью нечеткого множества
Понятие «богатый» часто используется при обсуждении социально-экономических проблем, в том числе и в связи с подготовкой и принятием решений. Однако очевидно, что разные лица вкладывают в это понятие различное содержание. Сотрудники Института высоких статистических технологий и эконометрики провели социологическое исследование представления различных слоёв населения о понятии " богатый человек".
Мини-анкета опроса выглядела так:
1. При каком месячном доходе (в млн. руб. на одного человека) Вы считали бы себя богатым человеком?
2. Оценив свой сегодняшний доход, к какой из категорий Вы себя относите:
а) богатые;
б) достаток выше среднего;
в) достаток ниже среднего;
г) бедные;
д) за чертой бедности?
3. Ваша профессия, специальность.
Всего было опрошено 74 человека, из них 40 - научные работники и преподаватели, 34 человека - не занятых в сфере науки и образования, в том числе 5 рабочих и 5 пенсионеров. Из всех опрошенных только один (!) считает себя богатым. Несколько типичных ответов научных работников и преподавателей приведено в табл.1, а аналогичные сведения для работников коммерческой сферы – в табл.2.
Таблица 1.
Типичные ответы научных работников и преподавателей
| Профессия (специальность) | Месячный доход в млн. руб для богатого | Категория на сегодняшний день | Пол |
| Преподаватель | Достаток ниже среднего | Ж | |
| Доцент | Достаток выше среднего | Ж | |
| Учитель | Достаток ниже среднего | М | |
| Старший научный сотрудник | За чертой бедности | М | |
| Инженер – физик | За чертой бедности | Ж | |
| Программист | Бедный | М | |
| Научный работник | Бедный | М |
Таблица 2.
Типичные ответы работников коммерческой сферы
| Профессия (специальность) | Месячный доход в млн. руб для богатого | Категория на сегодняшний день | Пол |
| Вице-президент банка | Богатый | Ж | |
| Зам. директора банка | Достаток выше среднего | Ж | |
| Начальник. кредитного отдела | Достаток выше среднего | М | |
| Начальник отдела ценных бумаг | Достаток выше среднего | М | |
| Главный бухгалтер | За чертой бедности | Ж | |
| Бухгалтер | Достаток ниже среднего | Ж | |
| Менеджер банка | Достаток выше среднего | М | |
| Начальник отдела проектирования | Достаток ниже среднего | Ж |
Разброс ответов на первый вопрос – от 1 до 100 млн. руб. в месяц на человека. Результаты опроса показывают, что критерий богатства у финансовых работников в целом несколько выше, чем у научных (см. гистограммы на рис.1 и рис.2 ниже).
Опрос показал, что выявить какое-нибудь конкретное значение суммы, которая необходима " для полного счастья", пусть даже с небольшим разбросом, нельзя, что вполне естественно. Как видно из таблиц 1 и 2, денежный эквивалент богатства колеблется от 1 до 100 миллионов рублей в месяц. Подтвердилось мнение, что работники сферы образования в подавляющем большинстве причисляют свой достаток к категории " достаток ниже среднего" и ниже (81% опрошенных), в том числе к категории " за чертой бедности" отнесли свой достаток 57%.
Со служащими коммерческих структур и бюджетных организаций иная картина: " бедная" - категория 1 человек (4%), " за чертой бедности" - категория 4 человека (17%), " доход выше среднего" - категория - 46% и 1 человек " богатая" - категория.
Пенсионеры, что не вызывает удивления, отнесли свой доход к категории " за чертой бедности" (4 человека), и лишь один человек указал " бедную" - категорию. Рабочие же ответили так: 4 человека - " доход ниже среднего", и один человек - " доход выше среднего".
Для представления общей картины в табл.3 приведены данные об ответах работников других профессий.
Таблица 3.
Типичные ответы работников различных профессий.
| Профессия (специальность) | Месячный доход в млн. руб для богатого | Категория на сегодняшний день | Пол |
| Работник торговли | Доход выше среднего | ж | |
| Дворник | Доход ниже среднего | ж | |
| Водитель | Доход ниже среднего | м | |
| Военнослужащий | Доход ниже среднего | м | |
| Владелец бензоколонки | Доход выше среднего | ж | |
| Пенсионер | За чертой бедности | ж | |
| Начальник фабрики | Доход выше среднего | м | |
| Хирург | Доход ниже среднего | м | |
| Домохозяйка | Доход ниже среднего | ж | |
| Слесарь-механик | Доход ниже среднего | м | |
| Юрист | Доход выше среднего | м | |
| Оператор ЭВМ | За чертой бедности | м | |
| Работник собеса | За чертой бедности | ж | |
| Архитектор | Доход выше среднего | ж |
Прослеживается интересное явление: чем выше планка богатства для человека, тем к более низкой категории относительно этой планки он себя относит.
Для сводки данных естественно использовать гистограммы. Для этого необходимо сгруппировать ответы. Использовались 7 классов (интервалов):
1 – до 5 миллионов рублей в месяц на человека (включительно);
2 – от 5 до 10 миллионов;
3- от 10 до 15 миллионов;
4 – от 15 до 20 миллионов;
5 – от 20 до 25 миллионов;
6 – от 25 до 30 миллионов;
7 – более 30 миллионов.
(Во всех интервалах левая граница исключена, а правая, наоборот – включена.)
Сводная информация представлена на рис.1 (для научных работников и преподавателей) и рис.2 (для всех остальных, т.е. для лиц, не занятых в сфере науки и образования - служащих иных бюджетных организаций, коммерческих структур, рабочих, пенсионеров).

Рис.1. Гистограмма ответов на вопрос 1 для научных работников и преподавателей (40 человек).

Рис.2. Гистограмма ответов на вопрос 1 для лиц, не занятых в сфере науки и образования (34 человека).
Для двух выделенных групп, а также для некоторых подгрупп второй группы рассчитаны сводные средние характеристики – выборочные средние арифметические, медианы, моды. При этом медиана группы - количество млн. руб., названное центральным по порядковому номеру опрашиваемым в возрастающем ряду ответов на вопрос 1, а мода группы - интервал, на котором столбик гистограммы - самый высокий, т.е. в него " попало" максимальное количество опрашиваемых. Результаты приведены в табл. 4.
Таблица 4.
Сводные средние характеристики ответов на вопрос 1 для различных групп (в млн. руб. в мес. на чел.).
| Группа опрошенных | Среднее арифметическое | медиана | мода |
| Научные работники и преподаватели | 11, 66 | 7, 25 | (5; 10) |
| Лиц, не занятых в сфере науки и образования | 14, 4 | (5; 10) | |
| Служащие коммерческих структур и бюджетных организаций | 17, 91 | (5; 10) | |
| Рабочие | - | ||
| Пенсионеры | 10, 3 | - |
Построим нечеткое множество, описывающее понятие «богатый человек» в соответствии с представлениями опрошенных. Для этого составим табл.5 на основе рис.1 и рис.2 с учетом размаха ответов на первый вопрос.
Таблица 5.
Число ответов, попавших в интервалы
| № | Номер интервала | |||||||||
| Интервал, млн. руб. в месяц | (0; 1) | [1; 5] | (5; 10] | (10; 15] | (15; 20] | (20; 25] | (25; 30] | (30; 100) | [100; +∞) | |
| Число ответов в интервале | ||||||||||
| Доля ответов в интервале | 0, 257 | 0, 284 | 0, 176 | 0, 068 | 0, 081 | 0, 095 | 0, 027 | 0, 013 | ||
| Накопленное число ответов | ||||||||||
| Накопленная доля ответов | 0, 257 | 0, 541 | 0, 716 | 0, 784 | 0, 865 | 0, 960 | 0, 987 | 1, 000 |
Пятая строка табл.5 задает функцию принадлежности нечеткого множества, выражающего понятие " богатый человек" в терминах его ежемесячного дохода. Это нечеткое множество является подмножеством множества из 9 интервалов, заданных в строке 2 табл.5. Или множества из 9 условных номеров {0, 1, 2, …, 8}. Эмпирическая функция распределения, построенная по выборке из ответов 74 опрошенных на первый вопрос мини-анкеты, описывает понятие " богатый человек" как нечеткое подмножество положительной полуоси.
Попробуйте в качестве примера исследовать значения фактора «Уровень качества курса» с использованием нечетких множеств. Значение оценки, присваиваемой каждому курсу для фактора «Уровень качества курса», определяется на универсальной шкале [0, 1], где необходимо поместить значения переменной «Уровень качества курса»: НИЗКИЙ, СРЕДНИЙ, ВЫСОКИЙ. Степень принадлежности некоторого уровня вычисляется как отношение числа ответов, в которых он встречался для данного курса, к максимальному (для этого значения) числу ответов по всем курсам.
Был проведен опрос 100 экспертов об уровне качества 3-х электронных курсов. Каждому эксперту в процессе опроса предлагалось оценить с позиции потребителя ценность того или иного курса. Эксперты давали свою оценку для каждого курса по 3-х бальной шкале: низкий средний, высокий. Результаты опроса сведены в таблицу.
| Курс | Уровень качества | Кол-во экспертов, давших |
| Экономика | низкий | |
| Экономика | средний | |
| Экономика | высокий | |
| Гражданское право | низкий | |
| Гражданское право | средний | |
| Гражданское право | высокий | |
| Математика | низкий | |
| Математика | средний | |
| Математика | высокий |
Построим аналогично предыдущему таблицу для расчёта коэффициентов принадлежности курса к каждому из уровней качества.
| Оценка | Низкая | |||
| Курс | Число ответов | Доля ответов | Накопленное число ответов | Накопленная доля ответов |
| Экономика | 0, 185 | 0, 185 | ||
| Гражданское право | 0, 363 | 0, 548 | ||
| Математика | 0, 452 | 1, 0 | ||
| Оценка | Средняя | |||
| Курс | Число ответов | Доля ответов | Накопленное число ответов | Накопленная доля ответов |
| Математика | 0, 179 | 0, 179 | ||
| Экономика | 0, 321 | 0, 5 | ||
| Гражданское право | 0, 5 | 1, 0 | ||
| Оценка | Высокая | |||
| Курс | Число ответов | Доля ответов | Накопленное число ответов | Накопленная доля ответов |
| Гражданское право | 0, 163 | 0, 163 | ||
| Математика | 0, 306 | 0, 469 | ||
| Экономика | 0, 531 | 1, 0 |
Решение задач принятия решений с использованием теории нечётких множеств сводится к выбору альтернатив, удовлетворяющих всем заданным критериям со значениями функции принадлежности по каждому критерию, находящимися в заранее заданных пределах (определяется экспертами).
В ходе управления финансами очень часто возникает задача борьбы с неопределенностью, сопровождающей финансовые решения. Неопределенность эта двоякая: а) текущее состояние финансовой системы не может быть распознано с необходимой точностью; б) будущие показатели финансовой системы и ее внешнего окружения неизвестны вполне точно.
Нечеткие множества в этом смысле могут выступать как инструмент моделирования неопределенности, который базируется на известной мыслительной способности человека оперировать качественными категориями и оформлять свои логические выводы также в качественной форме.
Оценка качества — это квалиметрия. Характерные задачи квалиметрии в финансовом менеджменте: оценка риска банкротства предприятия, оценка надежности акций и облигаций, выбор управляющей компании, оценка перспективности приобретения недвижимости, стоимостная оценка банковских залогов и т.д.
Все оценки производятся на основе наблюдений и независимых оценок экспертов. Если же речь идет об операциях с будущими значениями финансовых факторов, то удобно моделировать эти факторы как нечеткие числа и функции. Тогда можно получить итоговые результаты моделирования и оценить риск того, что эти финансовые результаты окажутся ниже предустановленных нормативов.
Характерные приложения теории нечётких множеств к финансовому менеджменту следующие:
1. Анализ риска банкротства предприятия.
2. Оценка риска инвестиционного проекта.
3. Построение оптимального портфеля ценных бумаг и бизнесов.
4. Оценка справедливой стоимости объектов (в том числе объектов недвижимости).
5. Оценка инвестиционной привлекательности акций и облигаций.
6. Анализ необходимости и обоснованности IT-решений.
Выводы.
Теория нечетких множеств — раздел прикладной математики, посвященный методам анализа неопределенных данных, в которых описание неопределенностей реальных явлений и процессов проводится с помощью понятия о множествах, не имеющих четких границ
Нечеткое множество характеризуется функцией принадлежности, отображающей некоторое множество (носитель нечеткого множества) в отрезок [0; 1]. Значение функции принадлежности показывает степень принадлежности соответствующего элемента носителя рассматриваемому нечеткому множеству. Это значение меняется от 0 (полная непринадлежность) до 1 (полная принадлежность).
Решение задач принятия решений с использованием теории нечётких множеств сводится к выбору альтернатив, удовлетворяющих всем заданным критериям со значениями функции принадлежности по каждому критерию, находящимися в заранее заданных пределах (определяется экспертами).
|
|