
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнение (2.4) называют уравнением неразрывности (сплошности) потока для несжимаемой жидкости.
|
|
Для плавно изменяющегося потока вязкой жидкости, движущейся от сечения 1 к сечению 2, уравнение Д. Бернулли имеет вид:
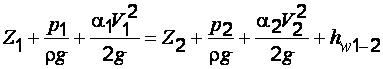 , (2.5)
, (2.5)
где 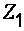 и
и 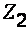 – расстояние от центров тяжести сечений 1 и 2 до произвольно выбранной горизонтальной плоскости сравнения;
– расстояние от центров тяжести сечений 1 и 2 до произвольно выбранной горизонтальной плоскости сравнения; 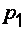 и
и 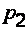 – давление в центрах тяжести живых сечений 1 и 2;
– давление в центрах тяжести живых сечений 1 и 2; 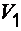 и
и 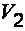 – средние скорости потока движущейся жидкости в рассматриваемых сечениях;
– средние скорости потока движущейся жидкости в рассматриваемых сечениях; 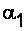 и
и 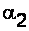 – коэффициенты Кориолиса (коррективы кинетической энергии), учитывающие неравномерность распределения местных скоростей по живому сечению потока жидкости. При турбулентном режиме движения
– коэффициенты Кориолиса (коррективы кинетической энергии), учитывающие неравномерность распределения местных скоростей по живому сечению потока жидкости. При турбулентном режиме движения 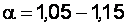 , а для ламинарного режима
, а для ламинарного режима 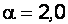 ;
; 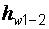 – потери напора на преодоление сил сопротивления при движении потока от сечения 1 до сечения 2.
– потери напора на преодоление сил сопротивления при движении потока от сечения 1 до сечения 2.
Для потока реальной жидкости уравнение Д. Бернулли является уравнением баланса энергии с учетом ее потерь. Заметим, что теряемая энергия не исчезает бесследно, а лишь превращается в другую форму (тепловую), т. е. теряется потоком безвозвратно.
Потери напора 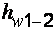 , отнесенные к единице длины, представляют собой гидравлический уклон
, отнесенные к единице длины, представляют собой гидравлический уклон
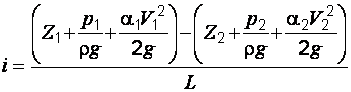 , (2.6)
, (2.6)
где 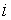 – гидравлический уклон,
– гидравлический уклон, 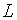 – расстояние между сечениями 1–1 и 2− 2.
– расстояние между сечениями 1–1 и 2− 2.
Различают два режима движения жидкости: ламинарный и турбулентный. Существование того или иного режима движения определяется поведением частиц жидкости.
Ламинарный режим движения характеризуется слоистым параллельно-струйчатым движением без перемешивания частиц жидкости и без пульсации скорости. При таком движении траектории частиц определяются формой русла, по которому течет жидкость.
Турбулентный режим движения характеризуется интенсивным перемешиванием жидкости с пульсацией скоростей и давлений. При таком движении частицы жидкости движутся по произвольным, крутящимся и колеблющимся, ежесекундно меняющим свой вид и направление траекториям.
Экспериментальными исследованиями О. Рейнольдса было установлено, что режим движения зависит от динамического коэффициента вязкости  , средней скорости движения
, средней скорости движения 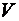 , плотности жидкости
, плотности жидкости 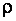 и диаметра трубопровода
и диаметра трубопровода 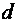 . Безразмерная величина, учитывающая влияние всех перечисленных факторов, названа числом Рейнольдса
. Безразмерная величина, учитывающая влияние всех перечисленных факторов, названа числом Рейнольдса
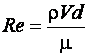 . (2.7)
. (2.7)
Известно, что динамический коэффициент вязкости  связан с кинематическим коэффициентом вязкости
связан с кинематическим коэффициентом вязкости 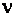 зависимостью
зависимостью 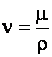 . Поэтому число Рейнольдса часто записывается в виде:
. Поэтому число Рейнольдса часто записывается в виде:
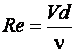 . (2.8)
. (2.8)
Формулы (2.7), (2.8) справедливы для круглых труб. Применительно к потокам любого другого сечения диаметр трубы выражают через гидравлический радиус 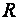 :
:
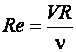 . (2.9)
. (2.9)
Границы существования того или иного режима движения жидкости определяются двумя значениямиRe: нижним критическим числом  и верхним
и верхним 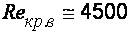 . При значении
. При значении 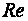 <
< 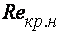 возможен только ламинарный режим, при
возможен только ламинарный режим, при 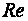 >
> 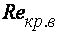 – только турбулентный режим, а при
– только турбулентный режим, а при 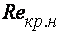 <
< 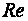 <
< 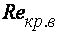 наблюдается неустойчивое состояние, называемое переходной зоной.
наблюдается неустойчивое состояние, называемое переходной зоной.
|
|