Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Ошибки, возникающие при выборочном наблюдении

Преимуществами выборочного метода наблюдения по сравнению со сплошным является: экономия всех видов ресурсов, снижение ошибок регистрации (расхождения между истинными и зарегистрированным значениями признака); незаменимость в случае, когда исследование связано с уничтожением наблюдаемых объектов. Основной недостаток выборочного метода – ошибки репрезентативности, возникающие только за счет того, что исследуется не вся совокупность, а лишь выборка из нее. Ошибки репрезентативности могут быть случайными и систематическими. Случайные ошибки возникают из-за того, что совокупность отобранных единиц наблюдения неполно воспроизводит всю совокупность в целом. Систематические ошибки возникают вследствие нарушения принципов случайного отбора единиц изучаемой совокупности.

Очевидно, что 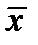тем точнее определяет параметр 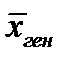, чем меньше абсолютная величина разности 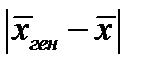. Другими словами, если и 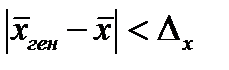, то чем меньше , тем оценка точнее. Таким образом, положительное число характеризует точность оценки и называется предельной ошибкой. Однако статистические методы не позволяют категорически утверждать, что оценка 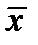удовлетворяет неравенству ; можно лишь говорить о вероятности, с которой это неравенство осуществляется.

Определение 9.5. Надежностью (доверительной вероятностью) оценки называют вероятность 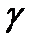, с которой осуществляется неравенство 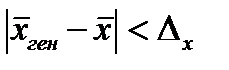. Обычно надежность оценки задается наперед, причем в качестве 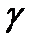берут число, близкое к единице. Наиболее часто задают надежность, равную 0, 95; 0, 99 и 0, 999.

Принцип практической уверенности: «Если какое-нибудь событие имеет малую вероятность (например, меньше 0, 01), то при единичном испытании можно практически считать, что это событие не произойдет, а если событие имеет вероятность близкую к единице (например, больше 0, 99), то практически при единичном испытании можно считать, что это событие произойдет наверняка.

Определение 9.6. Уровень значимости 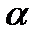– это максимальная вероятность ошибки, которой можно пренебречь в данной задаче или 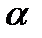– это вероятность того, что неравенство 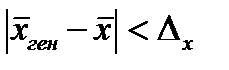не будет выполняться. Уровень значимости связан с надежностью следующим соотношением:

(9.1)

Величина предельной ошибки выборки в соответствии с теоремами теории вероятностей будет кратна средней ошибке. При большой выборке (): 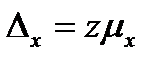, 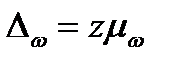; при малой выборке (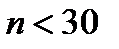): 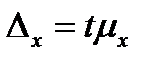, 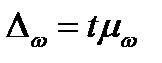. Число определяется из равенства 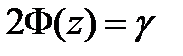, или 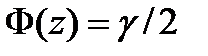; по таблице функции Лапласа находят аргумент 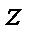, которому соответствует значение функции Лапласа, равное 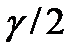. Число 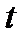– это критерий Стьюдента, который зависит от уровня значимости и числа степеней свободы (в данном случае 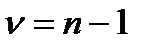). Для критерия Стьюдента также существуют специальные таблицы.

Предельная ошибка выборки позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы:

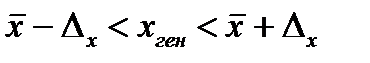(9.2)

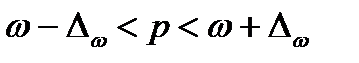(9.3)

При извлечении из генеральной совокупности выборок равного объема увеличение уровня надежности приводит к увеличению доверительного интервала. Для 100%-го уровня надежности доверительный интервал – 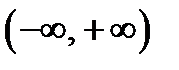. Для получения по возможности узкого интервала при сохранении высокого уровня надежности необходимо увеличить объем выборки. Интуитивно понятно, что чем больше информации, тем меньше неопределенность и больше точность.