
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 1. Системы линейных уравнений.
|
|
Задача 1. Решить систему линейных уравнений методом Жордана-Гаусса:
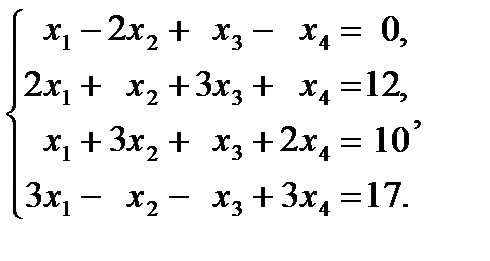
Решение. Метод Жордана-Гаусса - метод полного исключения неизвестных Систему можно решить, используя разные формы записи, например, в виде расширенной матрицы системы или в таблице Гаусса. Составим таблицу Гаусса. На первом шаге в качестве разрешающего (ведущего) элемента можно выбрать любой коэффициент 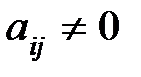 , например, an=1. Тогда первое уравнение (строка) разрешающее. На каждом шаге разрешающее уравнение делится на разрешающий элемент. Исключим соответствующую переменную x1из всех остальных уравнений путем элементарных преобразований. На каждом следующем шаге выбираем разрешающий элемент в уравнении, которое еще не было в качестве разрешающего. На втором шаге выберем разрешающий элемент а23=1. Исключим переменную х3из всех уравнений, кроме разрешающего (второго). Аналогично делаем еще два шага, исключая x 2и x 4(разрешающие элементы указаны в таблице).
, например, an=1. Тогда первое уравнение (строка) разрешающее. На каждом шаге разрешающее уравнение делится на разрешающий элемент. Исключим соответствующую переменную x1из всех остальных уравнений путем элементарных преобразований. На каждом следующем шаге выбираем разрешающий элемент в уравнении, которое еще не было в качестве разрешающего. На втором шаге выберем разрешающий элемент а23=1. Исключим переменную х3из всех уравнений, кроме разрешающего (второго). Аналогично делаем еще два шага, исключая x 2и x 4(разрешающие элементы указаны в таблице).
| №№ интерации | x 1 | x 2 | x 3 | x 4 | b |
| Исходная | 1 | -2 | -1 | ||
| система | |||||
| -1 | -1 | ||||
| -2 | |||||
| I | 1 | ||||
| -4 | |||||
| -7 | -4 | -12 | |||
| II | |||||
| 3 | |||||
| -1/3 | 4/3 | ||||
| III | |||||
| 5/3 | 10/3 | ||||
| - 5 | |||||
| IV | |||||
| -1 |
Таким образом, систему уравнений привели к виду: 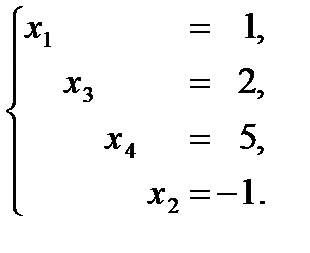
Система определена и имеет единственное решение: x= (1, -1, 2, 5).
Замечание. Случаи несовместной и неопределенной систем уравнений будет рассмотрен ниже при решении методом модифицированных жордановых исключений.
Задача 2. Решить систему уравнений методом модифицированных жордановых исключений (м.ж.и.).

Решение. Преобразуем систему к виду, удобному для применения м.ж.и.: 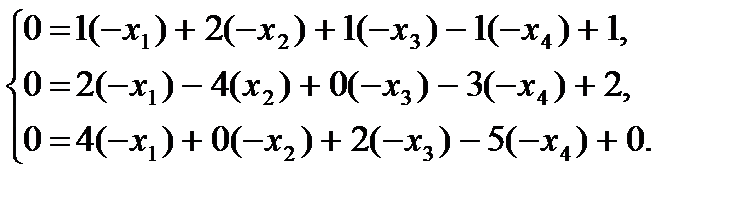
Запишем систему уравнений в виде таблицы:
| С Б | - x 1 | - x 2 | - x 3 | - x 4 | |
| 1 | -1 | ||||
| -4 | -3 | ||||
| -5 |
Проведем преобразования методом м.ж.и. указывая на каждом шаге разрешающий элемент (любой, отличный от нуля элемент основной части таблицы, т.е. кроме столба свободных членов). Переход от одной таблицы к другой, т.е. один шаг м.ж.и., проводится по правилам:
1. Разрешающий элемент a pqзаменяется обратной величиной: 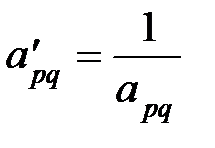 .
.
2. Остальные элементы разрешающей строки делятся на разрешающий элемент: 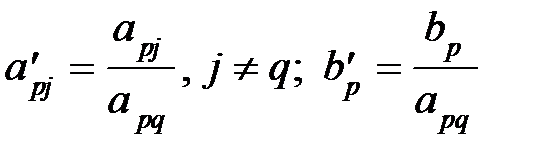 .
.
3. Остальные элементы разрешающего столба делятся на разрешающий элемент и меняют знаки: 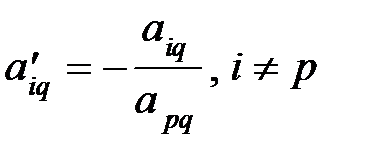 .
.
4. Все остальные элементы таблицы вычисляются по формулам (правило прямоугольника): 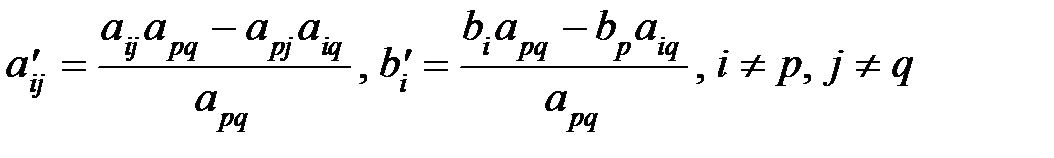 .
.
В результате одного шага м.ж.и. один нуль (в р -ой) строке переходит на верх таблицы, а на его место - соответствующая неизвестная (в q -ом столбе). Цель - перебросить все нули на верх таблицы.
Выберем разрешающий элемент 1. Следовательно, поменяются местами первый нуль и переменная х 1. Элементы новой таблицы посчитаем по четырем правилам м.ж.и. Например, вычислим элемент 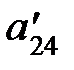 . Для элемента
. Для элемента 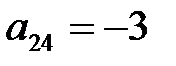 построим прямоугольник:
построим прямоугольник: 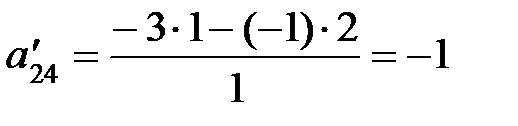
-1
2 -3
Столбы под переброшенными на верх нулями (разрешающие) будем опускать за ненадобностью, т.к. для нахождения неизвестных они должны быть умножены на нули. Проделаем возможное число шагов.
| С Б | - x 2 | - x 3 | - x 4 | |
| x 1 | -1 | |||
| -8 | -2 | -1 | ||
| -8 | -2 | -1 | -4 |
| С Б | - x 2 | - x 3 | |
| x 1 | |||
| x 4 | |||
| -4 |
В последней таблице все коэффициенты в третьей строке равны нулю, поэтому перебросить оставшийся нуль на верх таблицы нельзя. Так как свободный член в этой строке отличен от нуля (соответствующее уравнение: 0=0× (- х 2)+0× (- х 3) -4 Þ 0=-4), то система несовместна.
Указание. Проследить как преобразуется система уравнений за один шаг м.ж.и., для этого записать систему уравнений, соответствующие полученным таблицам. Сравнить с методом Жордана-Гаусса.
Задача 3. Найти все базисные решения системы уравнений:

Решение. Приведем систему к единичному базису; проделав возможное число шагов методом Жордана-Гаусса или жордановых исключений. Проведем преобразования методом м.ж.и. Запишем систему в виде таблицы и сделаем два шага.
| С Б |
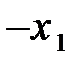
|
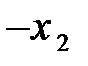
|
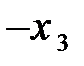
| С Б |
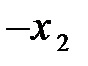
|
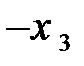
| С Б |
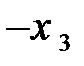
| |||||
| 1 | -2 | 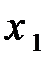
| -2 | 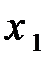
| -1 | 1/5 | |||||||
| -3 | 5 … | -5 | -2 | 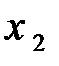
| -1 | -2/5 | |||||||
| Таблица №1 | Таблица №2 | Таблица №3 |
В таблице №3 система приведена к единичному базису, т.к. переменные х 1, х 2входят только в одно уравнение системы с единичными коэффициентами. Переменные х 1, х 2-базисные (основные), х 3- свободная (неосновная) переменная. Переменные х 1и х 2составляют один из базисов системы переменных х 1, х 2. Покажем, на данном примере, как записывается общее решение системы. Запишем систему, соответствующую таблице 3: 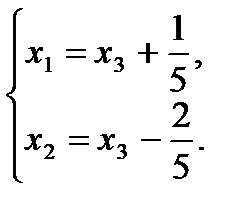 .
.
В данном случае число уравнений в системе, приведенной к единичному базису, r=2 (ранг системы уравнений), число переменных n =3; r < n, следовательно, система неопределенная. Получим общее решение, положив свободную переменную равной произвольному действительному числу, обозначив его через t: 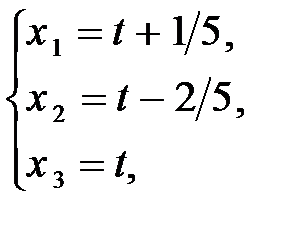 или другая форма записи:
или другая форма записи: 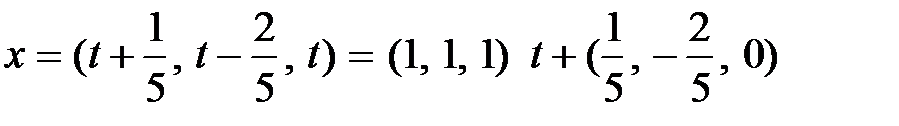 , где tÎ R. Система имеет бесконечное множество решений. Из этого множества выделим так называемые базисные решения. При нулевом значении свободной переменной х 3(
, где tÎ R. Система имеет бесконечное множество решений. Из этого множества выделим так называемые базисные решения. При нулевом значении свободной переменной х 3(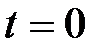 ) получаем одно из базисных решений:
) получаем одно из базисных решений: 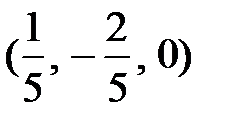 (это решение можно выписать из таблицы). Всего базисных решений может быть не более
(это решение можно выписать из таблицы). Всего базисных решений может быть не более 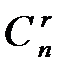 , т.е.
, т.е. 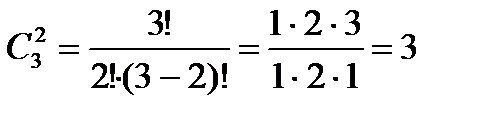 .
.
Другими базисами могут быть следующие группы переменных x 1, x 3; x 2, x 3(см. замечание). Взяв в таблице 3 разрешающим элементом а 21= -1. Перейдем от базиса х 1, х 2к базису х 1, х 3(таблица 4). Полагая свободную переменную х 2равной нулю (х 2=0), получим еще одно решение: 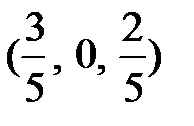 .
.
| C Б |
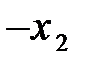
| С Б | 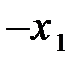
| ||||||
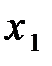
| -1 | 3/5 | 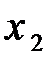
| -1 | -3/5 | ||||
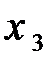
| -1 | 2/5 | 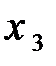
| -1 | -1/5 | ||||
| Таблица № 4 | Таблица № 5 |
Выбрав в таблице №4 разрешающий элемент 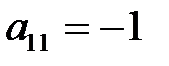 (или в таблице №3
(или в таблице №3 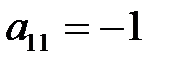 ), перейдем к базису
), перейдем к базису  (таблица №5). При
(таблица №5). При 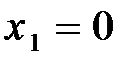 получим еще одно базисное решение:
получим еще одно базисное решение: 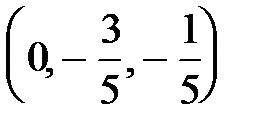 . Итак, данная система имеет три базисных решения:
. Итак, данная система имеет три базисных решения: 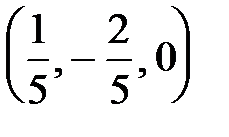 ,
, 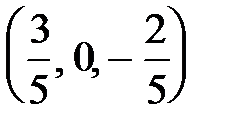 ,
, 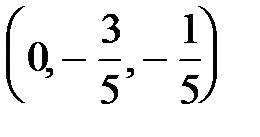 .
.
Замечание. Нетрудно заметить, что группа переменных составить базис не может, если при переходе к этому базису элемент, стоящий на пересечении соответствующей строки и столбца, равен нулю.
Задача 4. Решить матричным способом систему уравнений: 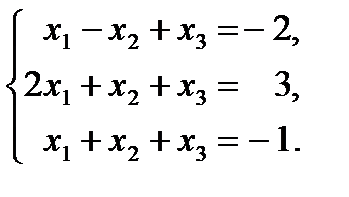
Решение. Введем в рассмотрение матрицы:
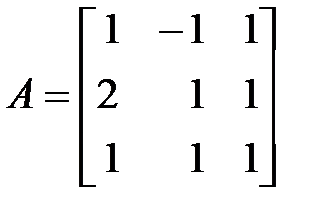 ,
, 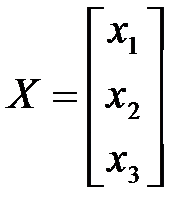 ,
, 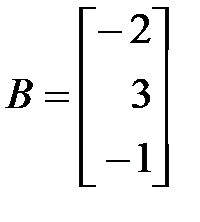 , где
, где 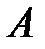 – матрица коэффициентов при переменных, а
– матрица коэффициентов при переменных, а 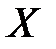 и
и 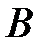 – матрицы-столбы переменных и свободных членов. Тогда систему можно записать в матричной форме
– матрицы-столбы переменных и свободных членов. Тогда систему можно записать в матричной форме 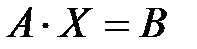 .
.
Найдем определитель матрицы 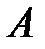 :
: 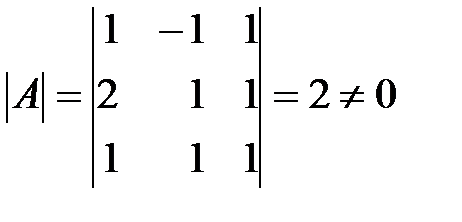 , т.е. матрица
, т.е. матрица 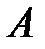 несобственная (невырожденная) и для матрицы
несобственная (невырожденная) и для матрицы 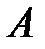 существует матрица обратная. Тогда решение матричного уравнения существует и представимо в виде
существует матрица обратная. Тогда решение матричного уравнения существует и представимо в виде 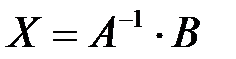 .
.
Найдем 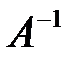 . Обратную матрицу можно найти путем элементарных преобразований или по формуле:
. Обратную матрицу можно найти путем элементарных преобразований или по формуле: 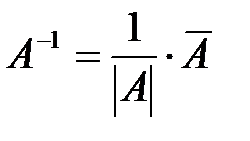 , где
, где 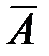 -матрица, присоединенная к матрице
-матрица, присоединенная к матрице 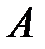 . Вычислим ее по формуле
. Вычислим ее по формуле 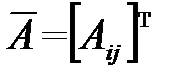 , где
, где  - алгебраические дополнения к элементам матрицы
- алгебраические дополнения к элементам матрицы 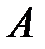 .
.
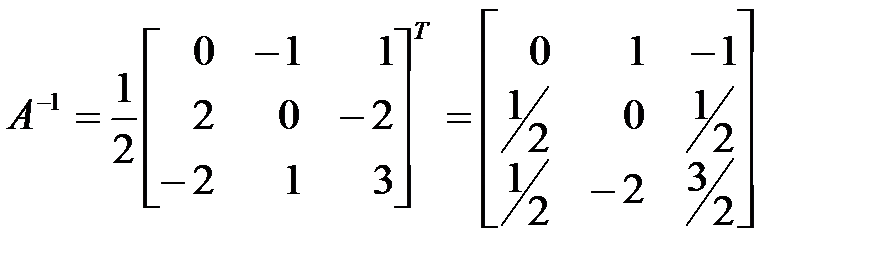 .
.
Рекомендуем проверить правильность нахождения обратной матрицы, исходя из ее определения, т.е. найти 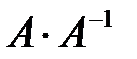 или
или 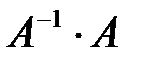 и убедиться в том, что получится матрица единичная.
и убедиться в том, что получится матрица единичная.
Следовательно, 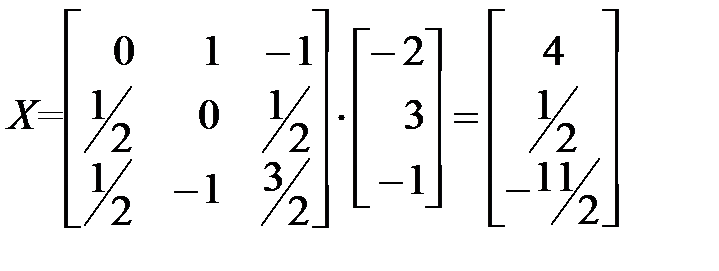 .
.
Система определена, имеет единственное решение: 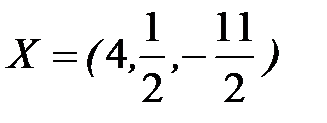 .
.
|
|