
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Преобразование координат
|
|
Пусть задано два базиса в пространстве Rn
1. 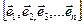
2. 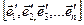
Любой вектор можно разложить по базисным векторам 1и2 системы:
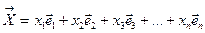
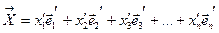 или
или 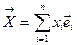 =
= 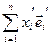
Найдем формулы преобразования координат одного и того же вектора 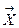 при переходе от одного базиса к другому.
при переходе от одного базиса к другому.
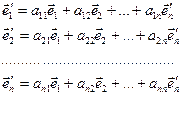
Или 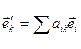 ,
, 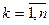
Из координат векторов 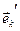 сформируем матрицу, называемую матрицей перехода от базис
сформируем матрицу, называемую матрицей перехода от базис 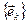 к базису
к базису 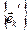
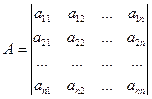
Т.к. базисные векторы 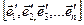 . линейно независимы, то матрица А будет невырожденной
. линейно независимы, то матрица А будет невырожденной 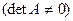 ..
..
Подставим 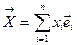 =
= 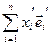 =
= 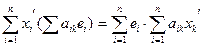
имеем 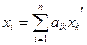 ,
, 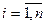 следовательно, (в развернутой форме) координаты вектора
следовательно, (в развернутой форме) координаты вектора 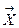 в первом базисе (x1, x2, x3, …xn) связаны координатами этого же вектора во втором базисе
в первом базисе (x1, x2, x3, …xn) связаны координатами этого же вектора во втором базисе 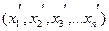 таким
таким
образом: 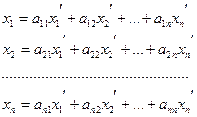 в матричной форме
в матричной форме
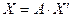 , где
, где 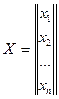 ,
, 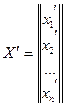 ,
, 
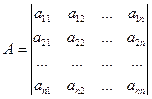
Т.к 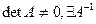 и
и 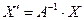 , следовательно переход от одного базиса к другому осуществляется при помощи умножения вектора на соответствующую матрицу.
, следовательно переход от одного базиса к другому осуществляется при помощи умножения вектора на соответствующую матрицу.
Пример. Пусть задан вектор 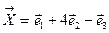 При помощи матрицы перехода
При помощи матрицы перехода 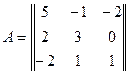 перейти к новому базису
перейти к новому базису 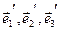 , т, е
, т, е
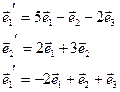 Найти вектор
Найти вектор 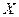 в новом базисе, т.е вектор
в новом базисе, т.е вектор 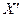
Решение: 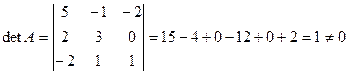
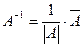 , т.к
, т.к 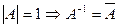
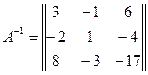
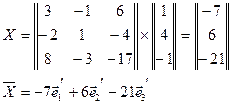
Провести обзор лекции в виде плана
Задание на самоподготовку: подготовить материал лекции к практическому занятию.
Лекцию подготовил преподаватель кафедры информатики и управления – Назаренко Г.В.
|
|