Ход работы. 1. Разобрать пример и записать в тетрадь

1. Разобрать пример и записать в тетрадь

2. В оргарф D (см. пример3) добавить петлю (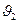, 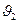) длины -1 и определить путь минимальной длины из 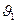в 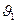в нагруженном орграфе D среди путей из 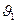в 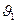, содержащих не более пяти дуг.

Отв: .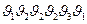

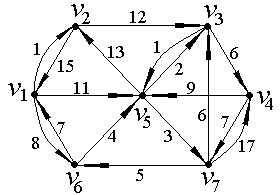
3. Найти пути минимальной длины а) из ν 1 во все остальные вершины среди путей, содержащих не более шести дуг; б) из ν 2 в ν 4 среди путей, содержащих не более четырех дуг;

∞ 5 ∞ 6 ∞ 10

∞ ∞ 2 ∞ -1 3

C(D) = ∞ ∞ ∞ ∞ ∞ ∞

∞ -3 ∞ ∞ ∞ ∞

∞ ∞ 1 2 ∞ ∞

∞ ∞ 5 ∞ ∞ ∞

2.Форма отчета

1.Выполнить представленные задания в тетради

2.Оценить свою работу по следующей схеме:

1 задание – 3 балла

2 задания – 4 балла

3 задания – 5 баллов

Задание на внеаудиторную самостоятельную работу

1. Найдем минимальный путь из вершины v₂ в v₆ в ориентированном нагруженном графе D

2. Ответить на контрольные вопросы

Контрольные вопросы.

1. Определение нагруженного орграфа

2. Определение длины пути

3. Определение минимального пути (маршрута) нагруженного орграфа (графа)

4. Свойства минимальных путей нагруженных орграфов (графов)

5. В каких случаях ненагруженные орграфы могут считаться нагруженными

6. Как задачу поиска минимальных путей можно свести к задаче поиска максимальных

Литература

1. В.Н. Нефедов «Курс дискретной математики»

г. Москва, изд. МАИ, 2010 год

2. В. Новиков «Курс дискретной математики для программистов»

г. Москва, 2012 год

3.М.С. Спирина, П.А. Спирин «Дискретная математика»- М.: Издательский центр «Академия», 2008 год