Критерий Вилкоксона.

💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Задачи, решаемые с помощью критерия Вилкоксона, аналогичны Т-тесту по независимым выборкам. Однако здесь не требуется интервальной шкалы.

Итак, пусть у нас имеется две группы значений некоторого признака. Ясно, что эти группы должны быть одинаковы по «смыслу», т.е. если в первой группе, например, рост в сантиметрах, то во второй группе – тоже рост в сантиметрах, а не вес в килограммах и не рост в миллиметрах. Наша задача – проверить, одинаковы ли средние показатели в этих группах.

Еще более правильно задачу сформулируем таким образом. Мы не знаем вид распределения, но хотим выяснить, одинаково ли распределение в обеих группах (выделенных из популяции). Если окажется, что распределение одинаково, то можно считать, что обе группы выбраны из одной и той же популяции. Тогда говорят, что популяция однородна.

Критерий Вилкоксона, как и критерий знаков, разберем на примере (взятом из классического учебника В.Е.Гмурмана «теория вероятности и математическая статистика»):

Пусть у нас имеется две группы данных. Например, в первой группе значения такие: 3, 4, 6, 10, 13, 17 (всего 6 значений). Во второй группе - 1, 2, 5, 7, 16, 20, 22 (т.е. 7 значений). Переписываем все 13 значений в порядке возрастания (помня, к какой группе относится каждое значение):

Очевидно, что если популяция является однородной, то и справа, и слева, и в центре этого ряда должны оказываться значения из обеих выборок, притом примерно в равной пропорции. На этом основана дальнейшая проверка. Определим ранги каждого элемента в общей выборке:

Теперь суммируем ранги той группы, в которой меньше значений. В нашем примере это 1-я группа, включающая N₁=6 значений. Сумма их рангов равна W=3+4+6+8+9+11=41. Это экспериментальное значение критерия Вилкоксона.

Теперь следует проверить гипотезу об однородности. Формулируем ее так: «Популяция однородна». Или так: «Параметры распределения обеих выборок одинаковы». Альтернативная гипотеза: «Параметры распределения выборок различны».

Проверку традиционно начинаем с выбора уровня значимости. Возьмем его равным α =0, 01. Так же, как и для критерия знаков, каждому уровню значимости однозначно соответствует интервал значений, внутри которого должно лежать экспериментальное значение W, если популяция однородна. Определить нижнюю границу этого интервала W_н можно из таблиц критерия Вилкоксона (см. Приложение 7).

Здесь следует еще раз напомнить, что альтернативные гипотезы бывают «односторонние» и «двусторонние». Поскольку альтернативная гипотеза у нас допускает отклонение в обе стороны, мы должны смотреть значение нижней критической точки в таблице не для α, а для Q=α /2=0.01/2=0.005. Это значение равно W_н=24.

Значение верхней критической точки находим из значения нижней критической точки по формуле:

Обратите внимание, что N₁ – это объем меньшей выборки, а не большей. Вычисляем: W_в = (6+7+1)·6 - 24 = 14·6 – 24 = 60.

Для проверки гипотезы осталось посмотреть, выполняется ли двойное неравенство W_н < W < W_в. У нас действительно, 24 < 41 < 60 выполнено, поэтому можно считать выборку однородной, а зависимость значений признака от номера группы – отсутствующей.

Таблицы значений критерия Вилкоксона существуют только для N₂ < 25. Если значение хотя бы одной выборки превосходит 25, то нижняя критическая точка вычисляется по-другому. Выбрав α, находят по таблице функции Лапласа такое значение z_кр, чтобы Ф(z_кр)=(1-α)/2. Например, для α =0, 05 (1-α)/2=(1-0, 05)/2=0, 475. По таблице подбираем, что Ф(z_кр)=0, 475 при значении z_кр=1, 96.

Удобно, что полученное таким образом значение не зависит от условий эксперимента, поэтому один раз получив, что для α =0, 05 z_кр=1, 96, можно в дальнейших аналогичных проверках уже не использовать таблицы функции Лапласа.

Теперь находим нижнюю критическую точку Wн. по формуле:

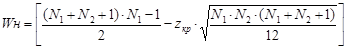
Например, для выборок с N1=25 и N2=30 и α =0, 05 значение нижней критической точки

Верхняя критическая точка ищется так же, как и для выборок объема < 25. В нашем примере она равна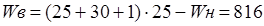