Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Значима ли величина коэффициента ранговой корреляции Кендалла?

Для этого требуется проверить гипотезу: «коэффициент ранговой корреляции Кендалла равен 0». Как и для коэффициента Спирмена, альтернативная гипотеза будет означать наличие значимой связи: «Коэффициент корреляции Кендалла отличен от 0».

Для проверки этой гипотезы нам потребуется использование функции Лапласа 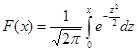(о ней рассказывалось при изучении нормального распределения). Сначала мы, как и при проверке любой гипотезы, выбираем уровень значимости, например, α =0, 05. Затем находим по таблице такой аргумент Z_крит, чтобы значение функции Лапласа F(Z_крит) было равно (1-α)/2. Сначала найдем, что 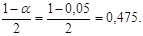Затем по таблице подбираем такое значение, чтобы F(Z_крит)=0, 475. Это значение Z_крит=1, 96. Если Вы пользуетесь не справочниками, а Excel, имейте в виду, что функция обратного нормального распределения вычисляет интеграл Лапласа не от 0 до x, а от -∞.

Найдя Z_крит, находим критическое значение коэффициента Кендалла τ _крит по формуле 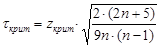, или в нашем примере

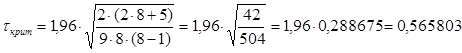
Осталось сравнить полученную величину коэффициента Кендалла с этим критическим значением. Поскольку экспериментальное значение 0, 642857 больше, чем критическое значение 0, 565803, мы отвергаем нулевую гипотезу и считаем, что коэффициент Кендалла в популяции не равен нулю, следовательно, между признаками существует связь. Тот же результат мы получили для данного примера и при использовании коэффициента Спирмена.