Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Нормальное распределение.

Если на случайную величину влияет очень много независимых случайных факторов, влияние каждого из которых по отдельности незначительно, то эта случайная величина будет иметь нормальное распределение, причем независимо от того, какие распределения имеют влияющие на нее факторы.

Изложенное выше – суть центральной предельной теоремы. Поскольку на мнение респондентов как правило влияет много независимых причин, нормальное распределение в социологии встречается очень часто.

Функция нормального распределения имеет вид: .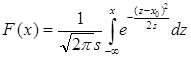

А такова плотность нормального распределения: .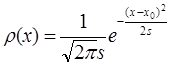

Функция и плотность нормального распределения зависят от двух параметров, обозначенных как x₀ и s. Параметр x₀ определяет сдвиг распределения и имеет смысл среднего значения случайной величины (максимальное значение плотности распределения достигается при x=x₀). Величина s определяет толщину «хвостов» распределения, т.е. разброс значений относительно среднего и имеет смысл стандартного (стандартного) отклонения.

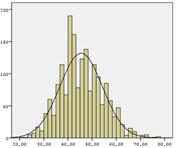
Вот так выглядит график функции и плотности нормального распределения:

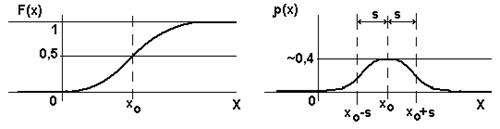
При нормальном распределении примерно 2/3 всех значений случайной величины лежат в пределах [x₀-s; x₀+s]. А в пределах [x₀-3s; x₀+3s] лежат 98, 5% всех значений, т.е. практически все значения. Это свойство называется «правилом трех сигм». Его применяют для проверки нормальности распределения: если значительная часть событий имеет значения, отличающиеся от среднего более, чем на 3 стандартных отклонения, то распределения не является нормальным. Для более точной проверки того, является ли распределение нормальным, используют методы статистической проверки гипотезы (например, критерий хи-квадрат Пирсона).

Кривая нормального распределения при x₀=0 и s=1 называется кривой Гаусса. (Иногда кривую нормального распределения при других значениях x₀ и s тоже называют кривой Гаусса). В статистических справочниках, как правило, приводят значения функции и плотности именно для такого вида нормального распределения:

,

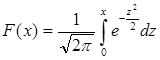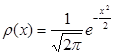
Интеграл для F(x) не вычисляется в элементарных функциях. Его значение смотрят в таблицах. Таблица значений F(x) приведена в Приложении 2 в конце этого пособия. Чтобы получить значение F(x), в которой интегрирование производится не от 0 до х, а от -∞ до х, надо к табличному значению функции прибавить 0, 5 (поскольку 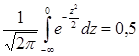). Чтобы найти 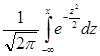для отрицательного х, следует табличное значение функции от |x| вычесть из 0.5. Значение плотности распределения ρ (x) можно вычислить на калькуляторе, подставив x в формулу.

Вероятность случайной величины попасть в заданный интервал [a; b] вычисляется как разность функций вероятности на концах интервала:

P([a; b])=F(b)-F(a)