
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретические упражнения
|
|
VII. КРАТНЫЕ ИНТЕГРАЛЫ
Теоретические вопросы
1. Определение двойного и тройного интегралов. Их геометрический и физический смысл.
2. Основные свойства двойных и тройных интегралов.
3. Теорема о среднем для двойного и тройного интегралов.
4. Вычисление двойных интегралов двумя последовательными интегрированиями (случай прямоугольной области).
5. Вычисление двойных интегралов двумя последовательными интегрированиями (общий случай).
6. Замена переменных в двойном интеграле.
7. Якобиан, его геометрический смысл.
8. Двойной интеграл в полярных координатах.
9. Тройной интеграл в цилиндрических координатах.
10. Тройной интеграл в сферических координатах.
Теоретические упражнения
1. Пользуясь определением двойного интеграла, доказать, что
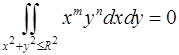 ,
,
если 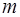 и
и 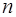 - натуральные числа, и, по меньшей мере, одно из них нечетно.
- натуральные числа, и, по меньшей мере, одно из них нечетно.
2. С помощью теоремы о среднем найти
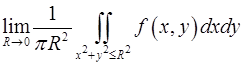 ,
,
где 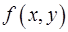 - непрерывная функция.
- непрерывная функция.
3. Оценить интеграл
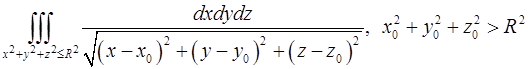 ,
,
т.е. указать, между какими значениями заключена его величина.
4. Вычислить двойной интеграл
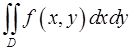 ,
,
если область 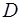 - прямоугольник {
- прямоугольник { 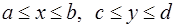 }, а
}, а 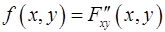 .
.
5. Доказать равенство
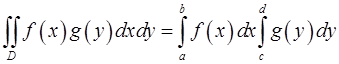 б
б
если область 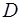 - прямоугольник {
- прямоугольник { 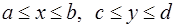 }.
}.
6. Доказать формулу Дирихле
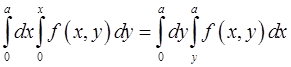 ,
, 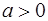 .
.
7. Пользуясь формулой Дирихле, доказать равенство
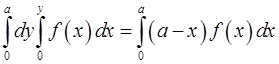 .
.
8. Какой из интегралов больше
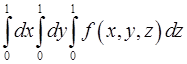 или
или 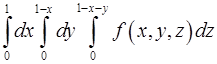 ,
,
если  ?
?
|
|