
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Явление резонанса. Резонанс напряжений.
|
|
Цепь переменного тока с последовательным соединением
Резистора, конденсатора и индуктивной катушки
| I |
| R |
| XL |
| Xс |
| Ua |
| UL |
| Uc |
| ~U |
Рисунок 1
Цепь переменного тока с последовательным соединением активного,
индуктивного и емкостного сопротивлений
Под действием приложенного напряжения в цепи протекает переменный ток.
На активным сопротивлении создаётся активное падение напряжения,
совпадающее по фазе с током: 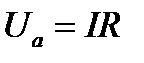 (1).
(1).
На индуктивном сопротивлении создаётся индуктивное падение напряжения опережающее по фазе ток на 900: 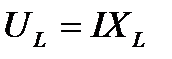 (2).
(2).
На емкостном сопротивлении создаётся емкостное падение напряжение,
отстающее по фазе от тока на 900: 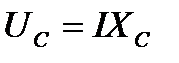 (3).
(3).
Результирующее напряжение на зажимах цепи в любой момент времени равно сумме мгновенных значений активного, индуктивного и емкостного падений напряжения: 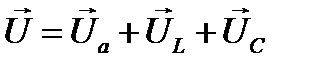 (4)
(4)
Действующее значение напряжение на зажимах цепи определяется как геометрическая сумма соответствующих напряжений на векторной диаграмме.
Прежде чем приступить к построению векторной диаграммы, необходимо указать, что в данной цепи возможны три режима:
а) Индуктивное сопротивление больше емкостного, т.е. 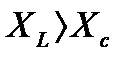
φ > 0, UL > UC. Ток отстает от напряжения на угол φ. Цепь имеет активно-индуктивный характер. Векторная диаграмма напряжений имеет вид (рисунок 2).
б) Индуктивное сопротивление меньше емкостного, т.е. 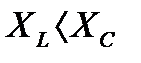
угол φ < 0, UL < UC. Ток опережает напряжение на угол φ. Цепь имеет активно-емкостный характер. Векторная диаграмма напряжений имеет вид, изображенный на рисунке 3.
в) Индуктивное сопротивление равно емкостному, т.е. 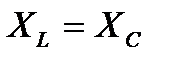
угол φ = 0, UL = UC. Ток совпадает с напряжением. Цепь имеет активный характер. Полное сопротивление z=R наименьшее из всех возможных значений XL и XC. Векторная диаграмма напряжений имеет вид, изображенный на рисунке 4.
а) Допустим, что индуктивное сопротивление больше емкостного сопротивления, следовательно, индуктивное падение напряжения больше емкостного падения напряжения.
Строить векторные диаграммы можно двумя способами (рисунок 2), при этом построение векторной диаграммы начинаем с вектора тока.
| U |
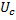
|
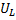
|
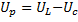
|

|
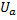
|
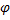
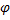
|
Векторная диаграмма тока и напряжений при 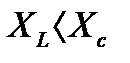
|
Векторная диаграмма тока и напряжений при 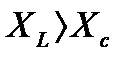
|
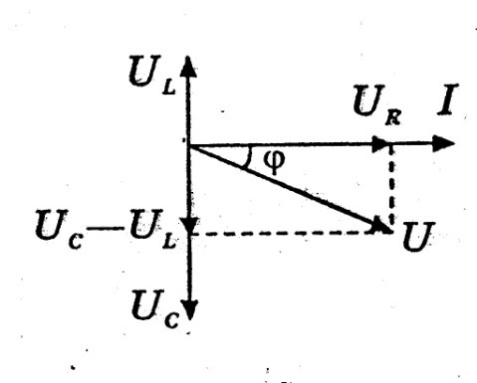
Рисунок 2
Вектор активного падения напряжения откладываем, как и вектор тока, в направлении начальной оси. Вектор индуктивного падения напряжения откладываем под углом 900 к начальной оси в сторону опережения, а вектор емкостного падения напряжения- под углом 900 в сторону отставания от тока.
Индуктивное падение напряжения и емкостное падение напряжения направлены в противоположную стороны т.е. находятся в противофазе.
Следовательно, геометрическое сложение 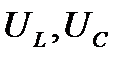 может быть заменено алгебраическим сложением.
может быть заменено алгебраическим сложением.
Условимся разность между 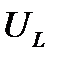 и
и 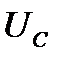 именовать реактивным падением напряжения:
именовать реактивным падением напряжения: 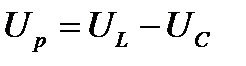
Для определения напряжения на зажимах необходимо геометрически сложить активное и реактивное падение напряжения.
Из векторной диаграммы следует, что ток отстаёт по фазе от приложенного напряжения на некоторый угол 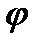 , т.е. цепь в целом имеет активно-индуктивный характер. Угол сдвига фаз положительный.
, т.е. цепь в целом имеет активно-индуктивный характер. Угол сдвига фаз положительный.
Выделяем из векторной диаграммы треугольник напряжений и определяем напряжение на зажимах цепи:
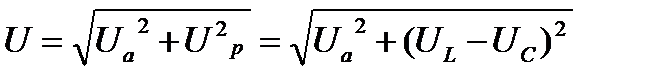 (5)
(5)
Разделив все стороны векторного треугольника напряжений на ток, переходим к треугольнику сопротивлений (рисунок 3).
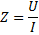
|
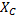
|
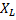
|
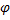
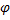
|
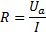
|
Xp
Рисунок 3. Треугольник сопротивлений.
Разность между индуктивным и емкостным сопротивлениями называется реактивным сопротивлением цепи и обозначается Хр: 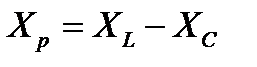 (6)
(6)
Следовательно, общее реактивное сопротивление цепи равно разности реактивных сопротивлений катушки и конденсатора.
Из треугольника сопротивлений определяем полноесопротивление цепи: 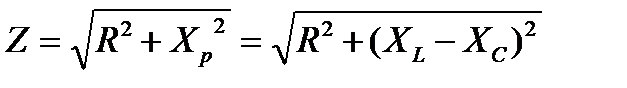 (7)
(7)
Угол сдвига фаз 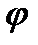 может быть определён графически на векторной диаграмме или аналитически по его тригонометрическим функциям:
может быть определён графически на векторной диаграмме или аналитически по его тригонометрическим функциям:
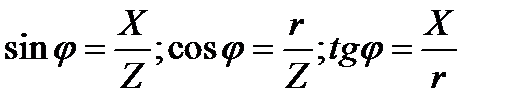 (8)
(8)
Закон Ома для данной цепи выражается формулой:
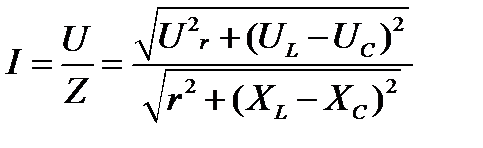 (9)
(9)
Из треугольника напряжений следует, что: 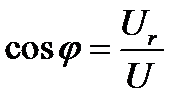 (9)
(9)
Из треугольника сопротивлений: 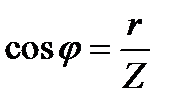 (10)
(10)
Умножив все стороны векторного треугольника напряжений на ток, переходим к треугольнику мощностей (рисунок 4).

|
|
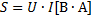
|
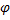
|
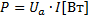
|
 = = 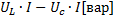
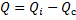 = = 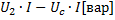 =
=
|
Рисунок 4 Треугольник мощностей
Явление резонанса. Резонанс напряжений.
Свойства цепи при резонансе напряжения.
1. Полное сопротивление последовательного контура при резонансе напряжений минимально и равно активному сопротивлению.
Из выражения (7) следует, что при резонансе когда 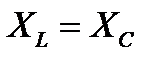 ,
, 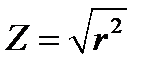 или
или 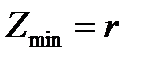 (рисунке 5).
(рисунке 5).
2. Ток в контуре при резонансе напряжений максимален и ввиду чисто активного сопротивления контура совпадает по фазе с приложенным напряжением.
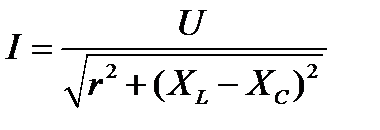 ; при
; при 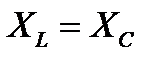 ,
, 
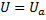
|
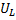
|
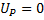
|

|
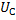
|
Рисунок 5. Векторная диаграмма тока и напряжений при 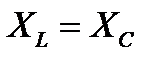
3. Напряжение генератора переменного тока, включенного в цепь расходуется на активном сопротивлении: 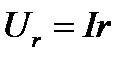 .
.
4.Напряжение на индуктивности и емкости определяется по закону Ома:
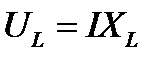 ;
; 
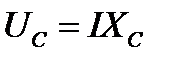 .
.
5. В последовательно соединенных сопротивлениях протекает одинаковый ток, при резонансе 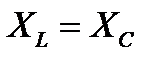 , и напряжения будут равны:
, и напряжения будут равны: 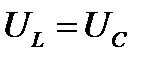 или
или 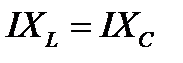 .
.
6. Если одновременно увеличить оба реактивных сопротивления 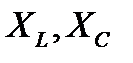 . То возрастут оба частичных напряжения
. То возрастут оба частичных напряжения 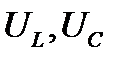 , а сила тока в цепи не изменится. Таким путём можно получить
, а сила тока в цепи не изменится. Таким путём можно получить 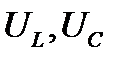 во много раз больше, чем напряжение цепи.
во много раз больше, чем напряжение цепи.
7. На векторной диаграмме видно, что напряжение на индуктивности и напряжение на ёмкости равны и сдвинуты по фазе друг относительно друга на 180 градусов и взаимно компенсируются (рисунок 5).
Угол сдвига фаз между током и напряжением при резонансе равен нулю. Это значит, что ток и напряжение совпадают по фазе (как в цепи с активным сопротивлением). Поэтому величина тока ограничивается только небольшим сопротивлением. 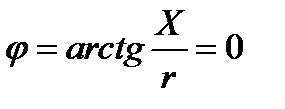
Вывод: Цепь носит активный характер, энергия полей в источник не поступает. Настройку контура в резонанс можно производить изменением либо индуктивности, либо ёмкости контура.
Наличие резонанса определяется:
- по наибольшему току в контуре;
- по наибольшему напряжению на его элементах.
|
|