Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Екінші ретті беттер

1. Сфера. Берілген нү ктеден бірдей қ ашық тық та орналасқ ан кең істіктегі нү ктелердің геометриялық орындарын сфералық немесе шар беті дейді. Оның канондық тең деуі:

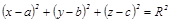
мұ ндағ ы 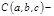сфераның центрі. Егер сфераның центрі 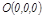нү ктесінде болса,

онда оның тең деуі мына тү рде болады: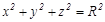

2. Цилиндр. Цилиндр перпендикулярлық қ имасындағ ы сызық тың тү ріне қ арай дө ң гелек, эллипстік, гиперболалық жә не параболалық цилиндрлер деп тө ртке бө лінеді.Осығ ан сә йкес тө менгі тең деулермен анық талады: , , , .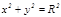

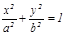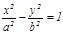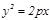Бұ л тең деулер жазық тық та шең берді, эллипсті, гиперболаны жә не параболаны кескіндейді, ал кең істікте цилиндрлердің тең деулері. Бұ л цилиндрлердің жасаушылары 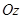ө сіне параллель болады.

Kонус

Kонус деп берілген нү ктеден ө тетін жә не бағ ыттаушы қ исық тың бойымен жылжитын жасаушы тү зудің ү здіксіз қ озғ алысынан шығ атын геометриялық бетті айтады. Оның тең деуі: 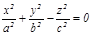. Бұ л конустың бағ ыттаушысы 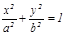эллипс, ал жасаушы тү зуі координаталардың бас нү ктесінен ө теді. Егер конустың перпендикулярлық қ имасы шең бер болса, онда оның тең деуі: 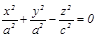болады; егер 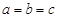болса, онда конустың тең деуі 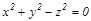болады.

4. Айналу беттері. Егер кең істікте бір сызық берілген ө сті айналса, оның айналуынан бет пайда болады. Айналушы сызық тың формасына байланысты бет ә р тү рлі болады. Мысалы, шең бер ө зінің диаметрі бойынша айналса, сфералық бет шығ ады, ал координаталар басынан ө тетін тү зу Oz ө сін айналса, дө ң гелек конус пайда болады. Сызық тың айналатын ө сін айналу ө сі, ал пайда болғ ан бетті айналу беті дейді.

5. Эллипсоидтың тең деуі: 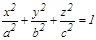, мұ ндағ ы 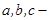жарты ө стер.Бұ л ү ш ө сті эллипсодтың тең деуі болады. 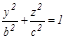эллипсін 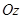ө сімен айналдырғ аннан шық қ ан бетті айналу эллипсоиды деп атайды. Оның тең деуі: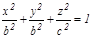

6. Бір қ уысты гиперболоид: .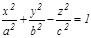

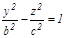гиперболасын 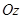ө сінен айналдырсақ бір қ уысты гиперболоид деп аталатын айналу беті шығ ады, оның тең деуі: .

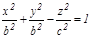7. Екі қ уысты гиперболоид: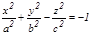

8. Эллипстік параболоид 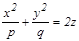, мұ ндағ ы .

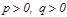9. Гиперболалық параболоид 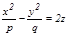, мұ ндағ ы .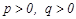