
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Эллипстің түрін оның жабайы теңдеуі бойынша зерттеу.
|
|
(4) тең деу бойынша эллипстің бірнеше қ асиеттерін анық тайық.. 
|
|
|
|
|

|

|
|
|
|
|





 1). (4) тең деудегі х пен у екінші дә режелі болғ андық тан, ол тең деуді М(х; у) нү ктесінің координаталарымен қ оса М1(х; -у), М2(-х; у), М3(-х; -у) нү ктелерінің де координаталары қ анағ аттандырады.
1). (4) тең деудегі х пен у екінші дә режелі болғ андық тан, ол тең деуді М(х; у) нү ктесінің координаталарымен қ оса М1(х; -у), М2(-х; у), М3(-х; -у) нү ктелерінің де координаталары қ анағ аттандырады.
|
|
|
|

 Ендеше эллипс координат осьтеріне,
Ендеше эллипс координат осьтеріне,
Координата басына қ арағ анда симметриялы.
2) у=0 болса, 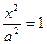 болады, бұ дан х = ± а. Сондық тан эллипс ох осін А1(-а; 0) жә не А2(а; 0) нү ктелерінде қ ияды. Ал х=0 болғ анда
болады, бұ дан х = ± а. Сондық тан эллипс ох осін А1(-а; 0) жә не А2(а; 0) нү ктелерінде қ ияды. Ал х=0 болғ анда 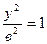 шығ ады да, у=± в. Демек, эллипс оу осін В1(0; -в), В2(0; в) нү ктелерінде қ ияды. Эллипстің осьтермен қ иылысу нү ктелері (А1, А2, В1, В2) тө белері деп аталады.
шығ ады да, у=± в. Демек, эллипс оу осін В1(0; -в), В2(0; в) нү ктелерінде қ ияды. Эллипстің осьтермен қ иылысу нү ктелері (А1, А2, В1, В2) тө белері деп аталады.
3) (4) тең деуден 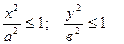 . Бұ дан |х| £ а жә не |у|£ в. Бұ дан – а £ х £ а жә не –в £ у £ в. Сө йтіп, эллипстің нү ктелері жазық тық тың қ абырғ алары 2а жә не 2в болатын тік тө ртбұ рышпен шектелген бө лігінде жатады.
. Бұ дан |х| £ а жә не |у|£ в. Бұ дан – а £ х £ а жә не –в £ у £ в. Сө йтіп, эллипстің нү ктелері жазық тық тың қ абырғ алары 2а жә не 2в болатын тік тө ртбұ рышпен шектелген бө лігінде жатады.
Теорема. Эллипстің кез келген М(х, у) нү ктесі ү шін тө мендегі қ атынас орындалады:
 r1 = a –
r1 = a – 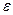 x, r2 = a +
x, r2 = a + 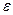 x.
x.
Дә лелдеу. Жоғ арыда r1 + r2 = 2a болатыны кө рестілген. Сонымен қ атар, геометьриялық кескіндеме бойынша:
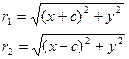 . Осы формулалардағ ы у2 –ты эллипстің канондық тең деуінен тауып алып, алдың ғ ы формулаларғ а қ ойып тү рлендірсек, тө мендегі тең дік шығ ады:
. Осы формулалардағ ы у2 –ты эллипстің канондық тең деуінен тауып алып, алдың ғ ы формулаларғ а қ ойып тү рлендірсек, тө мендегі тең дік шығ ады:
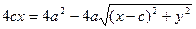
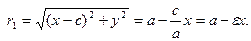
Дә л осылайша r2 = a + 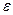 x.
x.
 Анық тама. x = a/
Анық тама. x = a/ 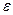 ; x= -a/
; x= -a/ 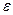 . тең деулерімен анық талатын екі тү зу эллипстің директрисалары деп аталады.
. тең деулерімен анық талатын екі тү зу эллипстің директрисалары деп аталады.
Теорема. Нү кте эллипсте жату ү шін оның фокусқ а дейінгі қ ашық тығ ының сә йкес директрисағ а дейінгі қ ашық тығ ына қ атынасы 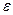 эксцентриситетке тең болуы қ ажетті жә не жеткілікті.
эксцентриситетке тең болуы қ ажетті жә не жеткілікті.
Мысал. 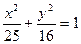 тең деуімен берілген эллипстің сол жақ фокусы мен тө менгі тө бесі арқ ылы ө тетін тү зудің тең деуін қ ұ р.
тең деуімен берілген эллипстің сол жақ фокусы мен тө менгі тө бесі арқ ылы ө тетін тү зудің тең деуін қ ұ р.
1) Эллипстің тө менгі тө бесінің координаталары: x = 0; y2 = 16; y = -4.
2) Сол жақ фокусының координаталары: c2 = a2 – b2 = 25 – 16 = 9; c = 3; F2(-3; 0).
3) Екі нү кте арқ ылы ө тетін тү зудің тең деуі:
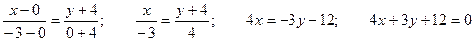
Мысал. F1(0; 0), F2(1; 1) фокустары мен ү лкен осі 2 –ге тең болатын эллипстің тең деуін жаз.
Эллипстің тең деуі мынадай: 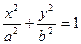 . Мұ нда а мен b жарты ө стерін табу керек. Фокустарының ара қ ашық тығ ы:
. Мұ нда а мен b жарты ө стерін табу керек. Фокустарының ара қ ашық тығ ы:
2c = 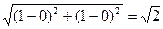 , сондық тан a2 – b2 = c2 = ½
, сондық тан a2 – b2 = c2 = ½
Есеп шарты бойынша 2а = 2, сонда а = 1, b = 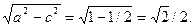
Сонымен эллипстің тең деуі: 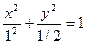 .
.
|
|