
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Процеси загибелі і розмноження.
|
|
Прикладом складання рівнянь для знаходження граничної вірогідності можуть служити процеси загибелі і розмноження, ГСП для яких має вигляд:
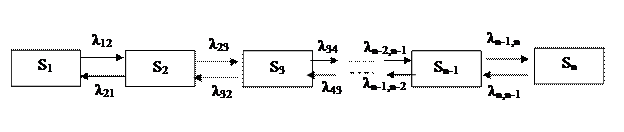
Рисунок 4.3 - ГСП для процесу розмноження і загибелі
Запишемо рівняння алгебри для вірогідності станів. У стаціонарних умовах для кожного стану інтенсивність потоку, впадаючого в цей стан, повинна дорівнювати інтенсивність потоку, витікаючого з цього стану.
Для першого стану S1 маємо:
λ 12 p1 = λ 21p2 (4.10)
Для другого стану S2 суми членів, які відповідають стрілкам, що входять і виходять, дорівнюють:
λ 23 p2 + λ 21p2 = λ 12 p1 + λ 32p3
Але за 4.10 можна скоротити справа і ліворуч рівні один одному члени і тоді отримаємо:
λ 23 p2 = λ 32p3
і далі, абсолютно аналогічно:
λ 23 p2 = λ 43p4
і т. д.
Очевидно, для цього випадку члени, що відповідають стрілкам, що стоять один над одним, рівні між собою:
λ k-1, k pk-1 = λ k, k-1pk (4.11)
де k набуває усіх значень від 2 до n.
Отже, гранична вірогідність станів:
р = (р1, р2...., рn)
у будь-якій схемі розмноження і загибелі задовольняють рівнянням:
λ 12 p1 = λ 21p2
λ 23 p2 = λ 32p3
λ 34 p3 = λ 43p4 (4.12)
λ k-1, k pk-1 = λ k, k-1pk
λ n-1, n pn-1 = λ n, n-1pn
і нормованій умові (4.9):
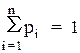
Рішення цієї системи має вигляд:
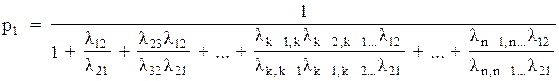
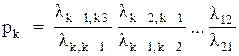 p1, k = 2, 3,... (4.13)
p1, k = 2, 3,... (4.13)
Приклад.
Технічний пристрій складається з трьох однакових вузлів, кожен з яких може виходити з ладу (відмовляти). Вузол, що відмовив, негайно починає відновлюватися. Необхідно знайти вірогідність числа вузлів, що відмовили.
Рішення.
Стани системи:
S1 - усі три вузли справні:
S2 - один вузол відмовив (відновлюється), два справні;
S 3 - два вузли відновлюються, один справний;
S 4 - усі три вузли відновлюються.
ГСП має вигляд:
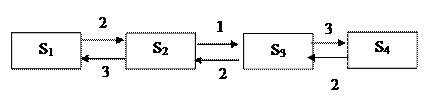
З графу видно, що процес, який протікає в системі, є процесом розмноження і загибелі.
По формулах (4.13) отримуємо
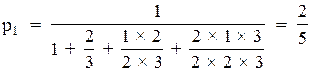
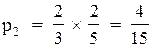
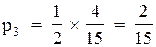
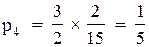
4.4 Порядок виконання роботи і методичні вказівки з її виконання.
У роботі вимагається провести розрахунок системи, що складається з n вузлів. Кожен з вузлів може знаходитися в справному або несправному стані. Після виходу вузла з ладу він починає негайно відновлюватися. Процес, що протікає в системі, можна вважати марківським. Усі вузли однотипні. Це означає, що усі вони мають одні і ті ж значення інтенсивностей виходу з ладу l і відновлення m.
Розрахунок на аналітичній моделі.
1. Відкрийте додаток Microsoft Excel і створіть книгу для проміжних і підсумкових даних по роботі.
2. Внесіть в таблицю початкові дані для свого варіанту, наприклад:
| Початкові дані | ||
| n | λ | μ |
| 0, 1 | 0, 2 |
.
3. Побудуйте розмічений ГСП процесу.
Очевидно, що розмічений ГСП системи є розміченим ГСП процесу загибелі і розмноження.
У разі, коли використовуються однотипні вузли, зручніше пронумерувати стан системи номерами, що відповідають числу несправних вузлів, тобто, 0, 1, 2,.n, де n - число вузлів. Тоді значення λ k-1, k і λ k, k-1 визначатимуться виразами:
λ k-1, k = (n – k) × λ, k = 0, 1,...n – 1
та
λ k-1, k = k × μ, k = 1, 2...n
де λ i μ є значення інтенсивностей виходу з ладу і відновлення вузла відповідно.
Використовуючи будь-який відомий графічний редактор намалюйте граф у вигляді малюнка на Excel - листі (у прикладі число вузлів дорівнює 6):
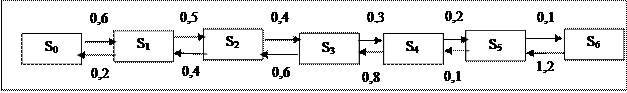
У разі утруднень з електронним зображенням допускається побудова ГСП в рукописному виді.
4. Проведіть розрахунок вірогідностей знаходження системи в кожному зі своїх станів за допомогою аналітичних виразів апарату марківських процесів.
Для проведення розрахунків створіть таблицю із структурою
| k | λ k, k+1 | λ k+1, k | П | Pk |
| Аналітич. модель | Імітац. модель |
у якій стовпці 1, 2,.6 використовуються таким чином:
1 - номер стану,
2 - інтенсивність переходу з цього стану в стан з номером на 1 більшим,
3 - інтенсивність переходу із стану з номером на 1 більшим в цей стан,
4 - значення кожного доданку, що стоїть у вираженні для обчислення Р0 (без 1),
5 - аналітично вичислені значення Рк,
6 - знайдені за допомогою імітаційної моделі значення Рк.
Таблиця повинна містити по одному рядку для кожного стану і один рядок для сум по стовпцях 4, 5, 6.
Точність для першого стовпця таблиці встановіть рівною одному десятковому знаку, для другого і третього - двом десятковим знакам, для четвертого, п'ятого і шостого - чотирьом десятковим знакам.
Експеримент на імітаційній моделі.
1. Встановіть режим запусків з експоненціально розподіленим часом обслуговування, задавши значення відповідного параметра рівним 1.
2. Знайдіть значення вірогідності знаходження системи в кожному зі своїх станів за допомогою імітаційної моделі. Результати прогонів занесіть в стовпець 6.
| Розрахунки та експеримент | |||||
| k | λ k, k+1 | λ k+1, k | П | Pk | |
| Аналітич. модель | Імітац. модель | ||||
| 0, 6 | 0, 0 | 3, 0000 | 0, 0878 | 0, 0882 | |
| 0, 5 | 0, 2 | 3, 7500 | 0, 2634 | 0, 2613 | |
| 0, 4 | 0, 4 | 2, 5000 | 0, 3292 | 0, 3267 | |
| 0, 3 | 0, 6 | 0, 9375 | 0, 2195 | 0, 2224 | |
| 0, 2 | 0, 8 | 0, 1875 | 0, 0823 | 0, 0837 | |
| 0, 1 | 1, 0 | 0, 0156 | 0, 0165 | 0, 0165 | |
| 0, 0 | 1, 2 | 0, 0014 | 0, 0012 | ||
| Σ | 10, 3906 | 1, 0000 | 1, 0000 |
Аналіз результатів.
1. Проаналізуйте результати, отримані теоретичним і експериментальним способами. Порівняєте результати між собою.
2. Побудуйте гістограми для вірогідності станів системи.
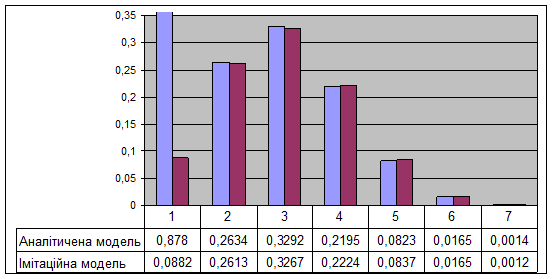
Завдання 1. Побудуйте матрицю переходів і визначите вірогідність станів через три кроки процесу для системи, що описується наступним ГСП:
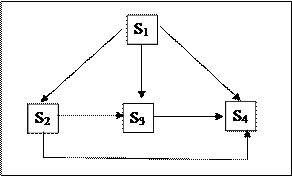
Вірогідність переходів має наступні значення Р12 = 0, 3; Р13 = 0, 4;
Р23 = 0, 1; Р24 = 0, 2; Р25 = 0, 3; Р45 = 0, 3; Р53 = 0, 2.
Завдання 2. Робляться три постріли по меті, яка може знаходитися в чотирьох станах:
- S1 - неушкоджена;
- S2 - незначно пошкоджена;
- S3 - отримала істотні ушкодження;
- S4 - повністю уражена.
Вірогідність переходу для трьох послідовних пострілів різна і задаються трьома матрицями:
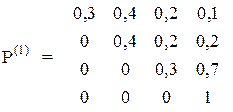
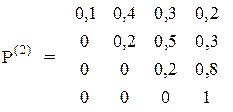
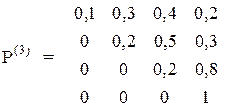
У початковий момент система знаходиться в стані S1.
Знайдіть вектор вірогідності Р(3).
Завдання 3. Пристрій S складається з двох вузлів A і B, кожен з яких в процесі роботи може відмовляти. Можливі наступні стани системи:
- S1 - обидва вузли працюють;
- S2 - вузол A відмовив, B працює;
- S3 - вузол B відмовив, A працює;
- S4 - обидва вузли відмовили.
Побудуйте ГСП системи (для двох випадків: можливість і неможливість одночасного виходу з ладу обох вузлів).
Завдання 4. Система S є пристроєм, що складається з двох вузлів A і B, кожен з яких може в якийсь момент часу відмовити. Вузол, що відмовив, негайно починає відновлюватися. Можливі такі стани системи:
- S1 - обидва вузли працюють;
- S2 - вузол A відновлюється, вузол B - працює;
- S3 - вузол A працює, вузол B відновлюється;
- S4 - обидва вузли відновлюються.
Побудуйте ГСП.
Завдання 5. В умовах завдання 4 кожен вузол перед тим, як почати відновлюватися, піддається огляду з метою локалізації несправності. Стани системи тепер нумеруватимемо не одним, а двома індексами: перший індекс означатиме стани вузла A:
1 - працює,
2 - оглядається,
3 - відновлюється;
другий індекс означатиме ті ж стани для вузла B.
(Наприклад, S23 означатиме, що вузол A оглядається, а вузол B - відновлюється.)
Побудуйте ГСП.
Завдання 6. Змініть програму (імітаційну модель) так, щоб вона забезпечувала знаходження значень граничної вірогідності для умов завдання 5.
Завдання 7. Розмічений ГСП системи S має вигляд
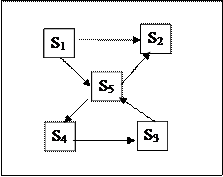
Складіть систему алгебраїчних рівнянь для знаходження граничної вірогідності.
Завдання 8. Побудуйте ГСП для знаходження вірогідності стану системи, вузли якої різнотипні, тобто, характеризуються різними значеннями λ і μ. Число вузлів нехай буде рівним 3, значення λ і μ. задайте довільно.
Проведіть розрахунок граничної вірогідності, після чого звірте його з результатами прогонів на імітаційній моделі.
Завдання 9. Здійсніть запуски програмної моделі, задавши для свого варіанту детермінований закон розподілу часу безвідмовної роботи або часу відновлення. Проаналізуйте результати.
Варіанти початкових даних
Число вузлів n = 4.
Інтенсивності відмов і відновлень:
| № | l | m |
| 0, 5 | 0, 3 | |
| 0, 5 | 0, 4 | |
| 0, 5 | 0, 5 | |
| 0, 5 | 0, 6 | |
| 0, 5 | 0, 7 | |
| 0, 5 | 0, 8 | |
| 0, 5 | 0, 9 | |
| 0, 5 | 1, 0 | |
| 0, 6 | 0, 3 | |
| 0, 6 | 0, 4 | |
| 0, 6 | 0, 5 | |
| 0, 6 | 0, 6 | |
| 0, 6 | 0, 7 | |
| 0, 6 | 0, 8 | |
| 0, 6 | 0, 9 | |
| 0, 6 | 1, 0 | |
| 0, 6 | 1, 1 | |
| 0, 7 | 0, 5 | |
| 0, 7 | 0, 6 | |
| 0, 7 | 0, 7 | |
| 0, 7 | 0, 8 | |
| 0, 7 | 0, 9 | |
| 0, 7 | 1, 0 | |
| 0, 7 | 1, 1 | |
| 0, 7 | 1, 2 |
4.5 Зміст звіту.
Звіт по роботі повинен включати:
- початкові ці роботи,
- розмічений ГСП процесу,
- таблицю з розрахунковими і експериментальними даними,
- гістограму граничної вірогідності.
4.6 Контрольні запитання і завдання.
1. Дайте визначення марківського процесу.
2. Як класифікуються марківські процеси?
3. Що таке граф станів і переходів (ГСП) Марківського ланцюга? Які бувають ГСП?
4. Що розуміється під матрицею перехідної вірогідності?
5. Як можна знайти вірогідність знаходження процесу в певному стані після певного числа кроків?
6. Що таке нестаціонарний марківський ланцюг?
7. Дайте визначення марківського процесу з безперервним часом і дискретними станами.
8. Що таке гранична вірогідність марківського процесу? Який фізичний сенс граничної вірогідності?
9. Як знайти граничну вірогідність системи, що має стаціонарний режим?
10. Що називається процесами загибелі і розмноження? Поясніть на ГСП.
11. Запишіть вираз для граничної вірогідності процесу загибелі і розмноження.
5 Моделі багатокритеріального вибору з урахуванням невизначеності початкової інформації
5.1 Мета роботи
Застосування теоретичних навичок при вирішенні проблеми прийняття рішень в умовах невизначеності на основі застосування продукційних правил нечіткої логіки.
5.2 Методичні вказівки по організації самостійної роботи студентів.
При підготовці до лабораторної роботи студенту необхідно ознайомитись з теоретичними основами нечітких множин та нечіткої логіки.
5.3 Опис методів лабораторної роботи
Лінгвістичної називається змінна, значенням якої є нечіткі підмножини, виражені у формі слів або пропозицій на природною або штучною мовою.
Формально лінгвістична змінна задається набором {X, T (X), G, M}, де X - назва цієї змінної; Т (Х) - терм-множина змінної X, тобто множина її значень; G - синтаксичне правило, породжує назви значень змінної X; М - семантична правило, яке ставить у відповідність кожному значенню лінгвістичної змінної її сенс.
Наприклад: змінна «вік» може включати терми: молодий, літній, старий.
На відміну від класичної теорії множин, що оперує поняттям приналежності й неналежності елемента множині, теорія нечітких множин допускає різну ступінь приналежності до них, яка визначається функцією приналежності елемента, значення якої змінюються в інтервалі [0, 1].
Таким чином, сенс лінгвістичного значення X характеризується деякою функцією приналежності μ: U = [0, 1], яка кожному елементу u U ставить у відповідність число з інтервалу [0, 1].
Процедура перетворення значень базової змінної в нечітку (лінгвістичну) змінну, що характеризується функцією належності, називається фазифікацією.
Приклад. У разі керування мобільним роботом можна ввести дві лінгвістичні змінні: < дистанція> (відстань до перешкоди) і < напрям> (кут між поздовжньою віссю робота та напрямком на перешкоду). Розглянемо лінгвістичну змінну < дистанція>. Значення її можна визначити термами: < далеко>, < середня (дистанція)>, < близько> і < дуже близько».
Для фізичної реалізації лінгвістичної змінної необхідно визначити точні фізичні значення термів цієї змінної.
Наприклад, невелика < дистанція> може приймати будь-яке значення з діапазону від нуля до нескінченності, а для її термів так, як показано на рис. 5.1.
Згідно з положеннями теорії нечітких множин, в такому випадку кожному значенню відстані з зазначеного діапазону може бути поставлено у відповідність деяке число від нуля до одиниці, яка визначає ступінь приналежності даної фізичної відстані (припустимо 40 см) до того чи іншого терму лінгвістичної змінної дистанція.
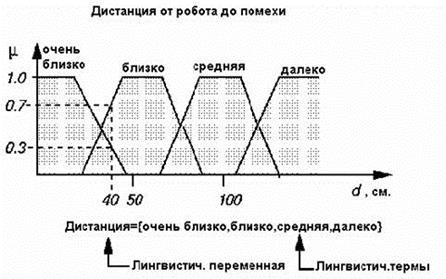
Рис. 5.1 - Лінгвістична змінна і функція приналежності
Ступінь приналежності визначається так званою функцією приналежності М(d), де d - відстань до перешкоди. У нашому випадку < відстані> 40 см. можна задати ступінь приналежності до терму < дуже близько", рівну 0, 7, а до терму < близько> - 0, 3.
Конкретне визначення ступеня приналежності може проходити при роботі з експертами.
Змінної < напрям>, яка може приймати значення в діапазоні від 0 до 360 градусів, задамо терми < ліве>, < прямо> і < праве>.
Тепер необхідно задати вихідні змінні. У розглянутому прикладі достатньо однієї, яка буде називатися < рульової кут>. Вона може містити терми: < різко вліво>, < вліво>, < прямо>, < вправо>, < різко вправо>.
При бажанні більш детального опису транспортного робота можна ввести і ще одну вихідну змінну - «лінійна швидкість».
Зв'язок між входом і виходом запам'ятовується в таблиці нечітких правил (рисунок 5.2).
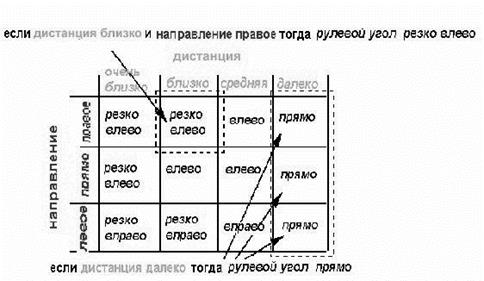
Рис. 5.2 – Таблиця нечітких правил
Кожен запис в даній таблиці відповідає своєму нечіткому правилу, наприклад:
Якщо < ДИСТАНЦІЯ БЛИЗЬКО> і < НАПРЯМОК ВПРАВО>, тоді < РУЛЬОВИЙ КУТ РІЗКО ВЛІВО>.
Таким чином, мобільний робот з нечіткою логікою буде працювати за наступним принципом:
▪ дані з сенсорів про відстань до перешкоди і направлення на неї повинні бути фаззіфіковані,
▪ оброблені згідно табличним правилам,
▪ дефаззіфіековані та отримані дані у вигляді керуючих сигналів надходять на привід керма робота.
Застосування традиційної нечіткої логіки в сучасних системах обмежено наступними факторами:
1) додавання вхідних змінних збільшує складність логічних виразів експоненціально;
2) як наслідок попереднього пункту, збільшується база правил, що призводить до важкої її розробці і сприйняття.
Основна структура і принцип роботи системи нечіткої логіки
Типова структура CHЛ, представлена на рис.5.3, складається з чотирьох головних компонентів: вхідний перетворювач чіткої змінної в нечітку (інша назва блок фазифікації, від слова fuzzy - нечіткий), база правил нечіткої логіки, блок нечіткого логічного висновку і вихідний перетворювач з нечіткою змінної в чітку (блок фазифікації)
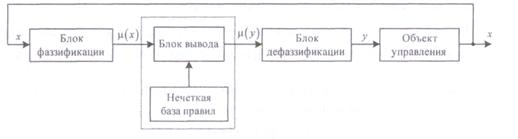
Рисунок 5.3. Типова структура системи управління з нечіткою логікою
Якщо вихідний сигнал блоку дефазифікації не є керуючим сигналом для об'єкта, то СНЛ буде системою прийняття рішення на базі нечіткої логіки.
Блок фазифікації здійснює перетворення виміряних реальних даних (наприклад, швидкості, температури, тиску і т.д.) у відповідні для цього значення лінгвістичних змінних.
Нечітка база правил містить експериментальні дані про процес управління і знання експертів в даній області. Блок виводу, що є ядром СНЛ, моделює процедуру прийняття рішення людиною. Організація виведення заснована на проведенні нечітких міркувань з метою досягнення необхідної стратегії управління.
Блок дефазифікації застосовується для вироблення чіткого рішення або дії, що управляє у відповідь на результати, отримані в блоці виводу.
У процесі функціонування СНЛ обчислюються значення керуючих змінних (або змінних впливу) на основі даних, одержуваних при спостереженні або вимірюванні змінних стану керованого процесу, для досягнення бажаної мети управління.
Слідуючи правилам завдання лінгвістичних змінних, вхідний вектор X і вектор вихідного стану Y, який містить можливі стани (або керуючі сигнали) об'єкта управління, можуть бути визначені відповідно як:
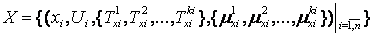 ; ;
| (5.1) |
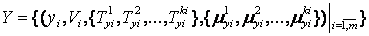 , ,
| (5.2) |
де x i - вхідні лінгвістичні змінні утворюють нечітка множина простір U = U 1 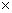 U 2
U 2 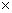 ...
... 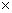 Un,
Un,
уi – вихідні лінгвістичні змінні утворюють нечітка множина - простір виходів V = V 1 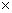 V 2
V 2 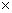 ...
... 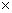 V m.
V m.
З рівнянь (5.1) і (5.2) випливає, що вхідні лінгвістична змінна хi в предметній області Ui характеризуються 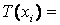
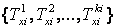 та
та 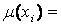
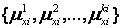 де
де 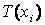 — множина термів для хi, тобто, множина імен значень лінгвістичної змінної х i, пов’язаних з кожним із значень.
— множина термів для хi, тобто, множина імен значень лінгвістичної змінної х i, пов’язаних з кожним із значень.
Наприклад, якщо х i означає швидкість, то 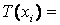
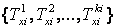 може означати {«дуже повільно», «повільно», «середньо», «швидко» і т.д.}.
може означати {«дуже повільно», «повільно», «середньо», «швидко» і т.д.}.
Аналогічно, вихідна лінгвістична змінна yi пов’язана з множиною 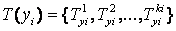 и
и 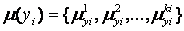 .
.
Розмір (або потужність) множини термів | 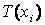 | = ki визначає число нечітких розбиттів вхідного простору на підмножини відповідно до обраної ступенем деталізації опису об'єкта управління. На рис. 1.4, а зображені три нечітких підмножини на інтервалі [-1, +1]. Випадок семи нечітких пересічних підмножин представлений на рис. 5.4, б.
| = ki визначає число нечітких розбиттів вхідного простору на підмножини відповідно до обраної ступенем деталізації опису об'єкта управління. На рис. 1.4, а зображені три нечітких підмножини на інтервалі [-1, +1]. Випадок семи нечітких пересічних підмножин представлений на рис. 5.4, б.
Зазвичай для пошуку оптимальної нечіткої декомпозиції вхідного і вихідного простору використовується евристичний метод проб і помилок, при цьому вибір вхідних і вихідних функцій приналежності заснований на суб'єктивних критеріях.
Зазвичай для пошуку оптимальної нечіткої декомпозиції вхідного і вихідного простору використовується евристичний метод проб і помилок, при цьому вибір вхідних і вихідних функцій приналежності заснований на суб'єктивних критеріях.
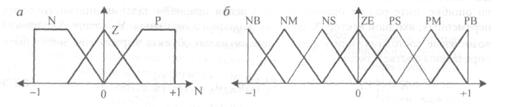
Рисунок 5.4 - Графічне представлення нечіткої декомпозиції:
а - груба нечітка декомпозиція з трьома нечіткими підмножинами: N - негативний, Z - нуль, Р - позитивний;
б - більш детальна нечітка декомпозиція з сімома компонентами: NB - негативний великий, NM - негативний середній, NS - негативний маленький, ZE - нуль, PS - позитивний маленький, РМ - позитивний середній, РВ - позитивний великий.
Фазифікація. Блок фазифікації виконує функцію перетворення чітких значень вхідних змінних у нечіткі. Таке перетворення фактично є свого роду нормуванням, необхідним для перекладу даних вимірювань в суб'єктивні оцінки. Отже, воно може бути визначене як відображення спостережуваних значень вхідних змінних у відповідні нечіткі.
У реальних СНЛ спостережувані дані зазвичай є чіткими (хоча вони можуть бути зашумлені). Природний і простий метод вхідного перетворення полягає в тому, щоб перетворити чітке значення х0 в нечіткий сінглетон (singleton) A.
Це означає, що функція приналежності 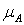 (х) буде дорівнювати 1 в точці х0 та нулю у всіх останніх точках. В даному випадку любе конкретне значення xi(t) в момент часу t відображається на нечітку множину
(х) буде дорівнювати 1 в точці х0 та нулю у всіх останніх точках. В даному випадку любе конкретне значення xi(t) в момент часу t відображається на нечітку множину 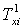 із значенням
із значенням 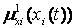 , а на нечітку множину
, а на нечітку множину 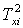 із значенням
із значенням 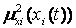 і т.д.
і т.д.
База правил нечіткої логіки. Правила нечіткої логіки представляються набором нечітких «IF-THEN» конструкцій, в яких передумови та висновку увазі використання лінгвістичних змінних.
Цей набір керуючих правил нечіткої логіки (або нечітких керуючих тверджень) характеризує зв'язок входу системи з її виходом. Загальна форма подання правил нечіткої логіки для випадку СНЛ з безліччю входів і одним виходом (MISO - «multi-input-single-output») така:
Ri: IF х is A i,..., AND у is В i THEN z = C i, i = 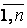 , ,
| ((5.3) |
де х,..., у та z — лінгвістичні змінні, що представляють змінні стану деякого керованого процесу та керуючі змінні відповідно;
Ai,.., Bi та Сi — лінгвістичні значення змінних х,..., у та z в предметних областях U,..., V та W відповідно. Варіант другої форми подання правил нечіткої логіки передбачає, що виведення представляється як функція змінних стану керованого процесу х,..., у, тобто
Ri: IF х is Ai,..., AND у is В i THEN z = 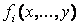 , i = , i = 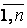 , ,
| ((5.4) |
де 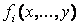 — функція змінних х,..., у стану управляємого процесу.
— функція змінних х,..., у стану управляємого процесу.
Нечіткі правила в рівняннях (1.3) і (1.4) обчислюють стан процесу (помилку визначення стану, інтегральну помилку стану і т.д.) в момент часу t і потім розраховують і приймають рішення про керуючих впливах, що реалізуються у вигляді функції змінних стану процесу (х,..., у).
Необхідно відзначити, що в обох видах правил нечіткої логіки вхідні змінні мають лінгвістичні значення, а вихідні мають або лінгвістичні значення.
Блок виводу. Блок виведення являє собою ядро СНЛ, що використовується для моделювання наближених міркувань і процесу прийняття рішень людиною в складних ситуаціях. Нечіткі висновки, нечіткі або наближені міркування - це найбільш важливі моменти при використанні коштів нечіткої логіки в управлінні складними об'єктами. Для організації нечітких висновків необхідно визначити поняття відносини.
Припустимо, що знання експерта А 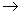 В відбиває нечітке причинне відношення передумови та ув'язнення, яке називається нечітким R: R = A
В відбиває нечітке причинне відношення передумови та ув'язнення, яке називається нечітким R: R = A 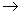 B.
B.
Майже всі реально працюючі прикладні системи, що використовують проміжні нечіткі оцінки, це системи, засновані на нечітких продукційних правилах. При виконанні нечітких висновків використовуються нечіткі відношення R, задані між однією областю (безліч X) та іншої областю (безліч Y) у вигляді непарного підмножини прямого твори X 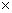 Y, що визначається за наступною формулою:
Y, що визначається за наступною формулою:
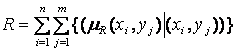 , ,
| ((5.5) |
де X = {х1, х2,..., хn] — область посилань;
Y = {у1, у2,..., уm) —область висновків;
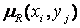 — функція приналежності
— функція приналежності 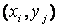 нечіткому відношенню R:
нечіткому відношенню R:
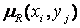
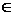 [0, 1], а знак
[0, 1], а знак 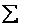 означає сокупність (об’єднання) множин.
означає сокупність (об’єднання) множин.
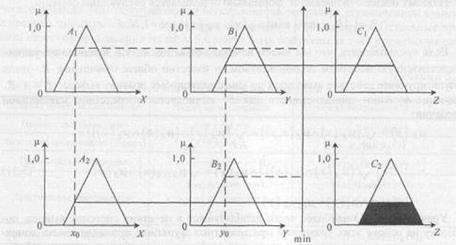
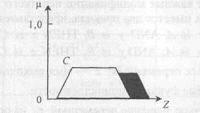
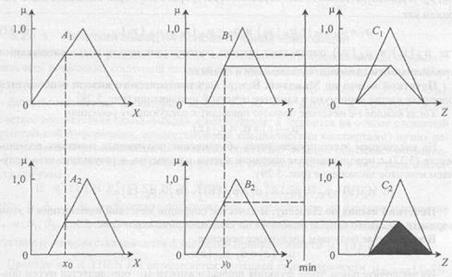
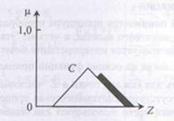
Рисунок 5.5. Ілюстрація отримання підсумкового результату нечіткого виводу по Ларсену
Дефазифікації. Під дефазифікації розуміється процедура перетворення нечітких величин, одержуваних у результаті нечіткого виводу, в чіткі. Ця процедура є необхідною в тих випадках, де потрібна інтерпретація нечітких висновків конкретними чіткими величинами, тобто коли на основі функції приналежності 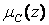 виникає потреба визначити для кожної точки в Z числові значення.
виникає потреба визначити для кожної точки в Z числові значення.
В даний час відсутня систематична процедура вибору стратегії дефазифікації. На практиці часто використовують два найбільш загальних методу: метод центру тяжіння (ЦТ - центроідний), метод максимуму (ММ).
Для дискретних просторів в центроідном методі формула для обчислення чіткого значення вихідної змінної представляється в наступному вигляді:
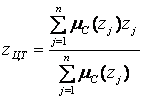 в загальному випадку в загальному випадку 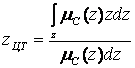 . .
| ((5.6) |
Стратегія дефазифікації ММ передбачає підрахунок всіх тих z, чиї функції приналежності досягли максимального значення. У цьому випадку (для дискретного варіанта) отримаємо
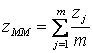 , ,
| ((5.7) |
де z — вихідна змінна, для якої функція приналежності досягнула максимуму; m — число таких величин.
З цих двох найбільш часто використовуваних стратегій дефазифікації, стратегія ММ дає кращі результати для перехідного режиму, а ЦТ - в сталому режимі через меншу середньоквадратичної помилки
5.4 Порядок виконання роботи і методичні вказівки по її виконанню
Розглянемо основні моменти нечіткого висновку за Мамдані.
Нехай дана система управління нечіткої логіки з двома правилами нечіткого управління:
Правило 1: IF x is A1 AND у is В1 THEN z is С1;
Правило 2: IF x is A2 AND у is В2 THEN z is C2.
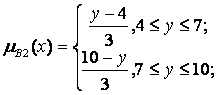
Припустимо, що величини х0 і у0, зчитувальні датчиком, є чіткими вхідними величинами для лінгвістичних змінних х та у і що задані такі функції приналежності для нечітких підмножин А1 А2, В1, В2, С1, С2 цих змінних:
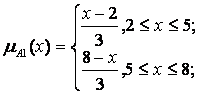
| 
|

| 
|
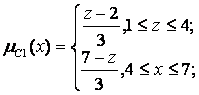
| 
|
Припустимо, що в момент часу t1 були зчитані значення датчиків х0(t1)=4 та y0(t1)=8. Проілюструємо, як при цьому буде обчислюватися величина вихідного сигналу.
Спочатку знаходимо 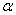 - зрізи для першого і другого правила на основі заданих функцій приналежності і з урахуванням значень х0 до у 0. З цією метою обчислюємо величини функцій приналежності в заданих точках для першого і другого правил:
- зрізи для першого і другого правила на основі заданих функцій приналежності і з урахуванням значень х0 до у 0. З цією метою обчислюємо величини функцій приналежності в заданих точках для першого і другого правил:
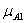 (x0 =4)=2/3 та
(x0 =4)=2/3 та 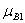 (y0 =8)=1;
(y0 =8)=1;
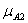 (x0 =4)=1/3 та
(x0 =4)=1/3 та 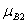 (y0 =8)=2/3.
(y0 =8)=2/3.
Потім відповідно до правила висновку за Мамдані (вибір мінімального значення функцій приналежності) визначаємо:
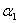 = min(
= min(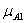 (x0),
(x0), 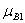 (y0)) = min(2/3, l) = 2/3;
(y0)) = min(2/3, l) = 2/3;
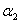 = min(
= min(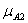 (x0),
(x0), 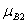 (y0)) = min(1/3, 2/3) = 1/3;
(y0)) = min(1/3, 2/3) = 1/3;
Результат застосування обчислених значень і до консеквент правила 1 (для С1) і правила 2 (для С2) показаний на малюнку 1.6.
Остаточний результат виходить шляхом об'єднання отриманих функцій приналежності з використанням оператора максимуму (з урахуванням стратегії виведення з Мамдані). Результуюча функція приналежності представлена на рис 5.6.
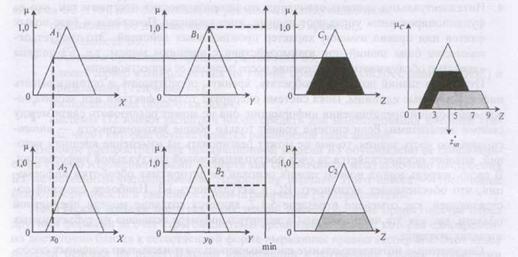
Рисунок 5.6. Ілюстрація нечіткого висновку за Мамдані в розглянутому прикладі
Для обчислення шуканої вихідної величини z проводимо дефазифікації нечіткої величини 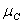 . За методом центру тяжіння отримуємо
. За методом центру тяжіння отримуємо
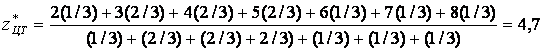 .
.
При використанні методу максимуму підрахуємо число значень z, при яких було досягнуто максимальне значення функцій приналежності 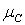 . Їх три — 3, 4 та 5 (із значенням функції приналежності 2/3). Таким чином,
. Їх три — 3, 4 та 5 (із значенням функції приналежності 2/3). Таким чином,
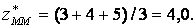
Функції та структура нечіткої системи
Нехай нечітка система здійснює вибір варіантів рішень на основі залежності вихідної величини від декількох вхідних величин. Припустимо, що математична модель залежності виходу від входів відсутня і замість неї використовується база експертних правил у вигляді нечітких висловлювань " if− then " у термінах лінгвістичних змінних та нечітких множин.
Тоді функціональність нечіткої системи прийняття рішень визначається такими кроками:
1) перетворення чітких вхідних змінних на нечіткі, тобто визначення ступеня відповідності входів кожній із нечітких множин;
2) обчислення правил на основі використання нечітких операторів та застосування імплікації для отримання вихідних значень правил;
3) агрегування нечітких виходів правил у загальне вихідне значення;
4) перетворення нечіткого виходу правил на чітке значення.
Структура системи з нечіткою логікою зображена на рисунку. Система побудована за схемою багатошарової штучної нейромережі, яка складається з вхідного, двох прихованих та вихідного шару.
Перший шар зображає входи системи, другий шар – нечіткі лінгвістичні змінні, третій шар – правила над нечіткими змінними, четвертий шар – виходи правил. Ваги усіх шарів, крім останнього, дорівнюють 1. Ваги зв’язків між шаром правил та вихідним шаром визначаються алгоритмом навчання.
Входи 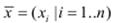 (наприклад, тиск, об’єм) та вихід y (наприклад, температура) є чіткими контрольованими величинами. Кожен параметр xi, i = 1…n має нечіткий відповідник у вигляді лінгвістичної змінної
(наприклад, тиск, об’єм) та вихід y (наприклад, температура) є чіткими контрольованими величинами. Кожен параметр xi, i = 1…n має нечіткий відповідник у вигляді лінгвістичної змінної 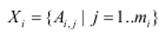 . Лiінгвістична змінна Xi складається з mi термів Ai, j, кожен з яких є нечіткою множиною.
. Лiінгвістична змінна Xi складається з mi термів Ai, j, кожен з яких є нечіткою множиною.
Правила Rk, k = 1..N перевіряють значення кожної лінгвістичної змінної, тому максимально можлива кількість правил дорівнює  . Реальну кількість правил позначимо через N ≤ Nmax.
. Реальну кількість правил позначимо через N ≤ Nmax.
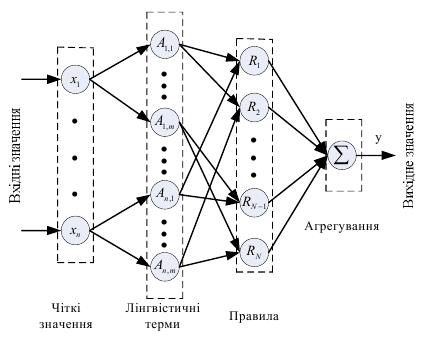
Рис. 5.7 – Структура системи нечіткого логічного виведення
Вихід правила – це лінгвістична змінна 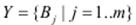 , яка набуває значення одного із термів Bj.
, яка набуває значення одного із термів Bj.
Для узагальнення правил відбувається агрегування їх нечітких виходів в одну нечітку множину з її подальшим перетворенням на чітке вихідне значення y.
Фазифікація входів
Фазифікація полягає у перетворенні чітких вхідних величин 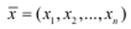 до нечітких множин A′ = (A1′, A2′, An′). У більшості випадків для цього використовуються синглетонні моделі.
до нечітких множин A′ = (A1′, A2′, An′). У більшості випадків для цього використовуються синглетонні моделі.
Синглетон чіткого значення xi є нечіткою множиною Ai′ (х, µAi′ (x)) з функцією належності

При фазифікації чіткого входу xi визначають ступені його відповідності кожному лінгвістичному терму Ai, j з функціями належності, j =1...m. Ці ступені є значеннями функцій належності µAi, j(xi) у точці x= xi, або інакше – значенням Ai, j(xi), i =1...n.
Нечітке логічне виведення
Нечіткі вхідні значення системи перетворюються на вихідні на основі правил нечіткої логіки, що характерно для експертних систем прийняття рішень. Нехай система прийняття рішень здійснює перетворення значень n вхідних лінгвістичних змінних 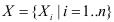 у вихідну лінгвістичну змінну Y = R (X) згідно з базою правил R = {Rk | k1 =..N}. Правила R акумулюють знання експертів у вигляді нечіткої імплікації R = A → B, яку можна розглядати як нечітку множину на декартовому добутку носіїв вхідних та вихідних розмитих множин. Процес отримання нечіткого результату B′ з нечітких вхідних множин A′ на основі знань A → B можна зобразити у такому вигляді
у вихідну лінгвістичну змінну Y = R (X) згідно з базою правил R = {Rk | k1 =..N}. Правила R акумулюють знання експертів у вигляді нечіткої імплікації R = A → B, яку можна розглядати як нечітку множину на декартовому добутку носіїв вхідних та вихідних розмитих множин. Процес отримання нечіткого результату B′ з нечітких вхідних множин A′ на основі знань A → B можна зобразити у такому вигляді
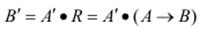 ,
,
де • – композиційне правило нечіткого виведення.
На практиці для нечіткого виведення використовується максимінна композиція, а нечітка імплікація реалізується знаходженням мінімуму функцій належності.
Для імітації роботи експертної системи за схемою імплікації використовується множина нечітких продукційних правил, кожне з яких будується у вигляді умовного оператора:
if логічний вираз then оператор,
де логічний вираз – висловлювання, побудоване на основі базових логічних операцій над нечіткими величинами; оператор – результуюче рішення. Правила можуть визначати відношення відповідності (is) між вхідними лінгвістичними змінними X та їх нечіткими термами 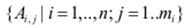 . Викоiристання нечітких умовних правил є природнім для подання знань експертами і спрощує їх машинне опрацювання.
. Викоiристання нечітких умовних правил є природнім для подання знань експертами і спрощує їх машинне опрацювання.
Загалом до правила можуть входити усі можливі комбінації лінгвістичних термів для усіх вхідних змінних, об’єднаних логічними операціями.
Слід зазначити, що за допомогою перетворень нечітких множин будь-яке правило, що містить у лівій частині як кон’юнкції, так і диз'юнкції, можна перетворити на систему правил, у лівій частині яких будуть або тільки кон’юнкції, або тільки диз'юнкції. Для визначення нечіткої кон’юнкції можна використати знаходження мінімуму, а для нечіткої диз'юнкції – знаходження максимуму двох функцій належності. Не зменшуючи загальності, будемо розглядати правила, побудовані на основі кон’юнкції.
Розрізняють дві моделі логічного виведення: Мамдані (Mamdani) та Такагі-Суджено (Takagi-Sugeno).
Модель Мамдані оперує лише з лінгвістичними змінними та нечіткими множинами і перетворює нечіткі входи на нечіткі виходи. Наприклад, для моделі Мамдані правила мають вигляд:
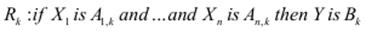
де Ai, k ∈ Xi – нечіткі множини для вхідних та Bk ∈ B – нечіткі множини для вихідної лінгвістичної змінної, які використовуються в k -му правилі (k =1..N). Операція and інтерпретується як t -норма нечітких множин.
Модель Такагі–Суджено оперує з чіткими величинами, лінгвістичними змінними та нечіткими множинами і перетворює чіткі входи у чіткі виходи. Правила моделі Такагі–Суджено можуть мати вигляд:
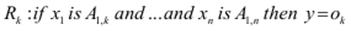 ,
,
де ok – завершальне значення k -го правила, вихідний сигнал або керуюча дія.
Для повноти бази нечітких правил повинні виконуватися такі умови:
1) для будь-якого терму вхідної змінної існує хоча б одне правило, в якому цей терм використовується у лівій частині правила;
2) існує хоча б одне правило для кожного лінгвістичного терму вихідної змінної.
Для багатовходових систем застосовується механізм логічного виведення, характерною рисою якого є використання рівнів істинності передумов правил.
Для кожного правила Rk, k =1..N визначається рівень його істинності α k стосовно входів. Рівень істинності є дійсним числом, яке характеризує ступінь відповідності нечітких входів системи Ai′, i =1..n заданим у правилах нечітким множинам Ai, j (j = 1.. mi):
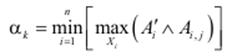 ,
,
де Xi – простір визначення входів Ai′, i =1..n; операція ∧ – нечітка кон’юнкція.
При використанні вхідних синглетонів механізм логічних виведень спрощується, оскільки ступінь істинності правил може бути визначений на основі фазифікованих входів:
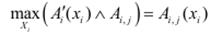 .
.
У цьому випадку обчислення рівня істинності k -го правила буде формуватися за формулою:
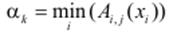 ,
,
Кожне із правил є нечіткою імплікацією, яка визначає вихідне значення залежно від рівня істинності лівої частини правила. Ступінь впевненості виведення задається функцією належності відповідного вихідного терму Bk. Використовуючи один зі способів побудови нечіткої імплікації, одержимо нові нечіткі змінні, або відповідні ступені впевненості в значенні виходів при застосуванні відповідного правила до заданих входів. Так, на основі визначення нечіткої імплікації за Мамдані, як мінімуму лівої й правої частин правила, маємо:
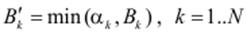 ,
,
де Bk′ – зрізи вихідних нечітких множин на рівні α k.
Завершальним кроком нечіткого логічного виведення є агрегування виходів правил. Один з основних способів акумуляції – нечітка диз’юнкція вихідних множин, або, інакше, знаходження максимуму отриманих функцій належності. Як результат, отримаємо значення агрегованого виходу:
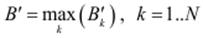
При нечіткому логічному виведенні паралельно опрацьовують велику кількість правил з подальшим їх агрегуванням у завершальне рішення. Правила можуть будуватися на основі досвіду та знань експертів, створенням моделі дій оператора, методом навчання. При проектуванні пристроїв з нечіткою логікою важливо забезпечити можливості їх пристосування до змін навколишнього середовища методом навчання бази правил за експериментальними даними. Навчання полягає в адаптивному підборі параметрів нечітких множин та автоматичному генеруванні правил нечіткого логічного виведення. Для цього використовуються алгоритми оптимізації та інтелектуального опрацювання даних – градієнтний, генетичний, штучних нейронних мереж, байесових мереж та ін.
Дефазифікація виходів
Після визначення індивідуальних виходів правил здійнюється дефазифікація агрегованого виходу. В загальному етап дефазифікації є необов’язковим і використовується за необхідності перетворення виведених нечітких лінгвістичних змінних до точного значення.
Існує декілька методів дефазифікації – метод среднього центру, перший максимум, середній максимум, висотна дефазифікація. Наприклад, метод середнього центру, або центроїдний метод, визначається центром ваги вихідної нечіткої множини:
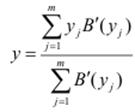 .
.
Для моделі Такагі–Суджено вихідні множини правил задаються у вигляді сінглетонів з функціями належності
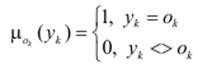 ,
,
де ok – вихідне значення k -го правила.
Тоді результуюче чітке вихідне значення системи прийняття рішень обчислюється зважуванням значень активованих правил:
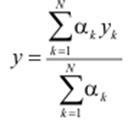 .
.
У системах керування отримане чітке вихідне значення використовується у контурі зворотного зв’язку для вироблення керуючих дій.
Приклад нечіткого виведення
Задача 1.
Нехай база нечітких правил прийняття рішень містить визначені експертами залежності шансу працевлаштування молодого спеціаліста від його рівня підготовки (рейтингу) та попиту на спеціалістів такого профілю на ринку праці. Введемо лінгвістичні змінні: рейтинг = (високий, низький); попит = (високий, низький); шанс = (високий, середній, низький).
Наведемо декілька із можливих правил:
R1: якщо попит є високим і рейтинг є високим, то шанс є високим;
R2: якщо попит є низьким і рейтинг є високим, то шанс є середнім;
R3: якщо попит є високим і рейтинг є низьким, то шанс є середнім;
Допустимо, що лінгвістичні терми входів описуються такими нечіткими множинами:
високий попит = {100/0.2; 200/0.4; 300/0.8; 400/1};
низький попит = {100/1; 200/0.8; 300/0.6; 400/0.4};
високий рейтинг = {50/0.1; 71/0.8; 88/0.9; 100/1};
низький рейтинг = {50/1; 71/0.3; 88/0.2; 100/0.1}.
Терми виходу описуються такими множинами:
високий шанс = {0/0.1; 0.5/0.5; 1/1};
середній шанс = {0/0.5; 0.5/1; 1/0.5}.
Необхідно визначити шанс працевлаштування при незначному попиті та середньому рейтингу.
Звернемо увагу на те, що вхідні дані не визначають термів незначний попит та середній рейтинг. Вихідну реакцію на ці нечіткі значення необхідно отримати в процесі логічного виведення на основі бази правил.
Нехай на вхід системи надходять нечіткі множини попиту A1′ = {100/0.4; 200/0.3; 300/0.2; 400/0.1} та рейтингу A2′ = {50/0.1; 71/0.8; 88/0.8; 100/0.1}.
Операції визначення мінімуму та максимуму позначимо у вигляді ∧ та ∨ відповідно.
Для обчислення виходу виконаємо етапи нечіткого логічного виведення:
1. Обчислення рівнів істинності правил.
α 1 = min[max(0.4^0.2, 0.3^0.4, 0.2^0.8, 0.1^1), max(0.1^0.1, 0.8^0.8, 0.8^0.9, 0.1^1)] = min[max(0.2, 0.3, 0.2, 0.1), max(0.1, 0.8, 0.8, 0.1)] = min[0.3, 0.8] = 0.3
α 2 = min[max(0.4^1, 0.3^0.8, 0.2^0.6, 0.1^0.4), max(0.1^0.1, 0.8^0.8, 0.8^0.9, 0.1^1)] = min[max(0.4, 0.3, 0.2, 0.1), max(0.1, 0.8, 0.8, 0.1)] = min[0.4, 0.8] = 0.4
α 3 = min[max(0.4^0.2, 0.3^0.4, 0.2^0.8, 0.1^1), max(0.1^1, 0.8^0.3, 0.8^0.2, 0.1^0.1)] = min[max(0.2, 0.3, 0.2, 0.1), max(0.1, 0.3, 0.2, 0.1)] = min[0.3, 0.3] = 0.3
2. Обчислення виходів правил.
B1′ = {0/min(0.3, 0.1), 0.5/min(0.3, 0.5), 1/min(0.3, 1)} = {0/0.1, 0.5/0.3, 1/0.3}
B2′ = {0/min(0.4, 0.5), 0.5/min(0.4, 1), 1/min(0.4, 0.5)} = {0/0.4, 0.5/0.4, 1/0.4}
B3′ = {0/min(0.3, 0.5), 0.5/min(0.3, 1), 1/min(0.3, 0.5)} = {0/0.3, 0.5/0.3, 1/0.3}
3. Агрегування виходів.
B′ =B1′ ∨ B2′ ∨ B3′ = {0/max(0.1, 0.4, 0.3), 0.5/max(0.3, 0.4, 0.3), 1/max(0.3, 0.4, 0.3)} = {0/0.4, 0.5/ 0.4, 1/0.4}
4. Дефазифікація виходу.
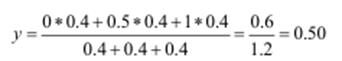
Отже, для заданих нечітких множин, при незначному попиті на спеціалістів та середньому кваліфікаційному рейтингу шанс працевлаштуватися становить 50 %.
Задача 2.
Задача розподілу інвестиційних ресурсів.
Є п’ять альтернативних проектів P = { Pi }, i =1, 5, та загальне бюджетне обмеження B, яке складає 50 тис. грн. Експертний комітет складається з чотирьох експертів D = { Dt }, t =1, 4. Необхідно у найкращий спосіб розподілити наявні бюджетні ресурси між запропонованими проектами.
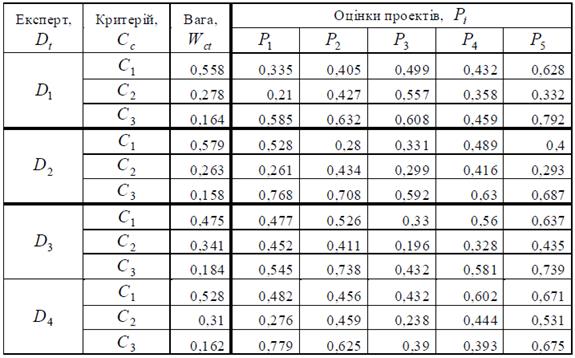
Кожний експерт Dt для кожного проекту Pi надає оцінки Sict за трьома критеріями C = { Cc }, c =1, 3:
C 1– прибутковість,
C 2– рівень виконавців проекту
C 3 – соціальна важливість проекту. Експерти D для критеріїв оцінювання C задають індивідуальні вагові коефіцієнти Wct.
Нормовані значення вагових коефіцієнтів критеріїв та критеріальні експертні оцінки проектів наведені в табл. 5.1.
Для одержання узагальнених оцінок проекту від кожного експерта, критеріальні оцінки кожного експерта агрегуємо за допомогою системи НЛВ із зваженою істинністю. Система НЛВ має 3 входи, що відповідають критеріям оцінювання та одне вихідне значення – ступінь привабливості проекту.
Таблиця 5.1 – Критеріальні експертні оцінки проектів
Лінгвістичні змінні, що відповідають вхідним значенням, мають по три
значення:
інтенсивність показника проекту = { мала, середня, велика }, та графічно показані на рис. 5.8.
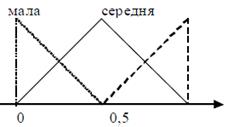
Рис. 5.8 – Лінгвістична змінна входу системи НЛВ
Лінгвістична змінна виходу системи НЛВ також має три
градації:
ступінь привабливості = { низька, середня, висока }, показана на рис. 5.9.
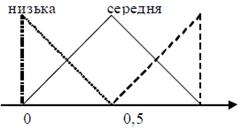
Рис. 5.9. Лінгвістична змінна виходу системи НЛВ
Для відповідних нечітких множин входу та виходу застосовуються трикутні функції належності. База правил системи НЛВ наведена в табл. 5.2.
Таблиця 5.2 – База правил прикладу
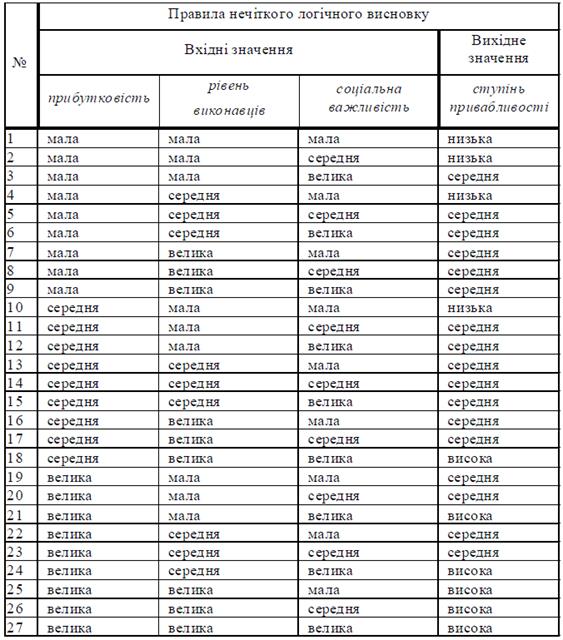
Ступінь виконання кожного правила визначається за формулою:
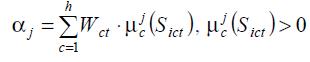 ,
,
а процедура імплікації за Мамдані 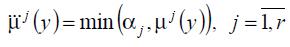 .
.
Розглянемо функціонування системи НЛВ із зваженою істинністю для одержання агрегованих значень оцінок експерта D 1для проекту P 1. У системі НЛВ для значень критеріальних оцінок з табл.1 експерта D 1 для проекту P 1 спрацювали правила 2, 3, 5, 6, 11, 12, 14, 15. В табл. 5.3 наведена процедура розрахунку значень істинності передумов та ступеню виконання для правил 2, 12, 14.
Таблиця 5.3 – Приклад виконання правил 2, 12, 14
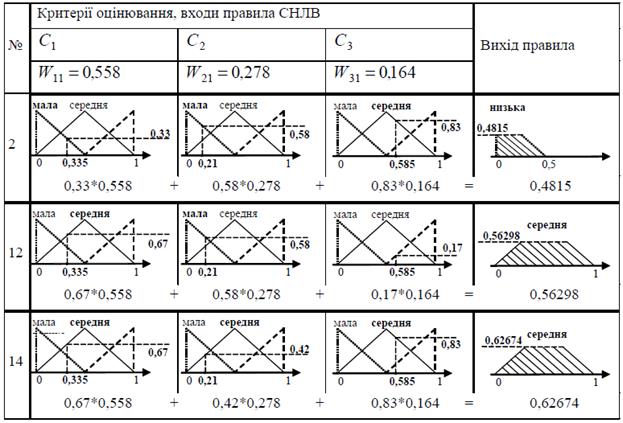
Значення агрегованих за допомогою системи НЛВ оцінок всіх експертів для всіх проектів наведені в табл. 5.4.
Таблиця 5.4 – Агреговані за допомогою системи НЛВ експертні оцінки проектів
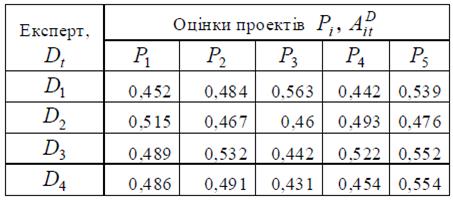
Тепер для подальшого розв’язку задачі знайдемо остаточну узагальнену оцінку кожного проекту – ступінь його привабливості для розподілу інвестиційних ресурсів. Рівень експертів будемо вважати однаковим, і розрахуємо ступені привабливості як середні значення агрегованих експертних оцінок проектів за формулою:
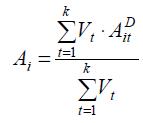 .
.
Результати наведені в табл. 5.5.
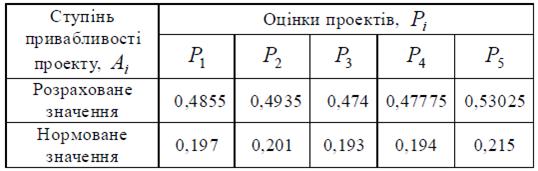
Таблиця 5.5 – Остаточні оцінки проектів
Таблиця 5.6 – Значення обсягів інвестування проектів
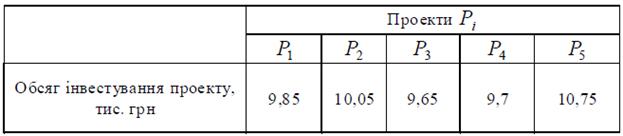
Відповідно до знайдених нормованих значень ступенів привабливості
проектів з табл. 5 на пропорційній основі визначимо значення інвестування кожного проекту виходячи з наявного бюджету B, що складає 50 тис. грн. (див.табл. 5.6).
5.5 Зміст звіту
1. Нехай база нечітких правил прийняття рішень містить визначені експертами залежності можливості залучення туристів в м. Севастополь від ціни путівки, рівня наданого сервісу та пори року. Вхідні данні встановлюються експертним шляхом.
2. Задача отримання максимальної ефективності від проведення рекламної компанії в залежності від виду засобів масової інформації, де буде розміщатись рекламна продукція.
Рекламу можна розміщувати в наступних засобах масової інформації: телебачення, газети, радіо, Інтернет. Загальний бюджет на рекламу товару становить 125 тис. грн. Створіть експертний комітет не менше ніж з трьох експертів з різним досвідом та різною обізнаністю з даної проблеми. Необхідно у найкращий спосіб розподілити наявні бюджетні ресурси на рекламу між запропонованими ЗМІ. Підтвердіть отримані висновки графічно та аналітично, застосовуючи алгоритми отримання підсумкового результату нечіткого виводу по Ларсену, за Мамдані та Такагі-Суджено.
5.6 Контрольні питання і завдання
1. Що таке СНЛ?
2. Що таке лінгвістичні змінні та як вони задаються?
3. Що називається фазифікацією?
4. Основна структура та функції СНЛ?
5. Які функції виконує блок фазифікації?
6. Що таке нечітка база правил і як вона формується?
7. Які функції виконує блок фазифікації?
8. Що таке терми і як формується множина термів?
9. Що називається потужністю множини термів?
10. Функції блоку виводу.
11. Алгоритм отримання підсумкового результату нечіткого виводу по Ларсену.
12. Алгоритм отримання підсумкового результату нечіткого виводу за Мамдані.
13. Алгоритм отримання підсумкового результату нечіткого виводу Такагі-Суджено.
ПЕРЕЛИК ПОСИЛАНЬ
1. Вентцель Е.С., Овчаров Л.А. Теория случайных процессов и ее инженерное приложение – М. «Наука» 1991.
2. Вентцель Е.С. Исследование операций: задачи, принципы, методология – М. «Наука» 1980.
3. Таха Ч. Введение в исследование операций. Том 1, 2.-М.»Мир» 1985.
4. Кофман А. Введение в теорию нечетких множеств. – М. Радио и связь. 1982.
5. Жлуктенко В.І., Наконечний С.І., Савіна С.С. Стохастичні процеси та моделі в економіці, соціології, екології. – К. 2002
6. Fuzzy Technology: основы моделирования и решения экспеертно-аналитических задач. – К.: Эльга, Ника-Центр, 2003. – 296 с.
7. Fuzzy Technology: модальность и принятие решения в маркетинговых коммуникациях. – К: Ника-Центр, Эльга, 2002. – 224 с.
8. Экономико-математические методы и прикладные модели: Учеб. пособие для ВУЗов / Под ред. В.В. Федосеева. - М.: ЮНИТИ, 2001. - 391 с.
9. Дубров A.M. Моделирование рисковых ситуаций в экономике и бизнесе: Учеб. пособие / Под ред. Б.А. Лагоши. - М.: Финансы и статистика, 2000. - 176 с.
10. Экономико-математические методы и прикладные модели: Учебно-методическое пособие / В.А. Половников, И.В. Орлова, А.Н. Гармаш, В.В. Федосеев. -М.: Финстатинформ, 1997.
11. С.Д.Штовба " Введение в теорию нечетких множеств и нечеткую логику"
12. Бережная Е.В. Бережной В, И. Математические методы моделирования экономическиъ систем: Учеб пособие. 2-е изд., перераб и доп. – М.: Финансы и статистика, 2006.– 432 с.
13. Лабскер Л.Г. Вероятностное моделирование в финансово-экономической области – М.: Альпина Паблишер, 2002. – 224 с.
Навчальне видання
МЕТОДИЧНІ ВКАЗІВКИ
до лабораторних робіт з дисципліни
" Прикладні задачі моделювання економічних процесів"
для студентів усіх форм навчання
спеціальності " Економічна кібернетика"
Упорядники Кирій Валентина Василівна
Фастова Наталя Іванівна
Відповідальний випусковий В.О. Тімофєєв
Редактор
Комп’ютерна верстка
План 20, поз.
Підпис. до друку Формат 60 84 1\16. Спосіб друку -
Умов. друк. лист. Облік. вид. лист. Тираж прим.
Зам. № Ціна договірна
 |
ХНУРЕ. Україна. 61166 Харків, просп. Леніна, 14

Віддруковано в навчально-науковому
видавничо-поліграфічному центрі ХНУРЕ
61166 Харків, просп. Леніна, 14
|
|