Студопедия

Главная страница Случайная страница

Разделы сайта

АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника






  • Как продвинуть сайт на первые места?
    Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.
    Ускорение продвижения
    Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.
    Начать продвижение сайта

    • Принтер 250


    ⇐ ПредыдущаяСтр 2 из 4Следующая ⇒




    принтер | сканер 450

    поскольку последнее число равно сумме двух предыдущих, можно сразу же придти к выводу, что в этом сегменте сети нет сайтов, на которых ключевыми словами являются одновременно принтер и сканер:

    принтер & сканер 0

    диаграмма Эйлера для этого случая показана на рисунке справа:

    2) с этого момента все просто: для того, чтобы определить, сколько сайтов удовлетворяют заданному условию

    достаточно просто сложить числа, соответствующие запросам принтер & монитор и
    сканер & монитор

    3) таким образом, правильный ответ: 40 + 50 = 90.

    Возможные проблемы: · обратите внимание, что в условии была лишняя информация: мы нигде не использовали количество сайтов в данном сегменте Интернета (1000) и количество сайтов с ключевым словом монитор (450) · не всегда удается «раскрутить» задачу в уме, здесь это несложно благодаря «удачному» условию

    Решение (вариант 3, таблицы истинности):

    1) для сокращения записи обозначим через C, П, М высказывания «ключевое слово на сайте – сканер» (соответственно принтер, монитор)

    2) если рассматривать задачу с точки зрения математической логики, здесь есть три переменных, с помощью которых можно составить всего 8 запросов, выдающих различные результаты

      С П М
    ?      
    ?      
    ?      
    ?      
    ?      
    ?      
    ?      
    ?      
    всего      

    3) составим таблицу истинности, в которую добавим левый столбец и последнюю строку, где будем записывать количество сайтов, удовлетворяющих условиям строки и столбца (см. рисунок справа); например, первая строка соответствует сайтам, на которых нет ни одного из заданных ключевых слов; такая схема непривычна, но она существенно упрощает дело

    4) сумма в последней строчке получается в результате сложения всех чисел из тех строк первого столбца, где в данном столбце стоят единицы. Например, сумма в столбце С – складывается из четырех чисел в последних четырех строчках первого столбца. Мы пока не знаем, сколько результатов возвращает каждый из восьми запросов отдельно, поэтому в первом столбце стоят знаки вопроса

    5) добавим в таблицу истинности остальные запросы, которые есть в условии, в том числе и тот, который нас интересует:

    П | С = принтер | сканер 450

    П & М = принтер & монитор 40

    Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
    Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM. SeoHammer делает продвижение сайта прозрачным и простым занятием. Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
    Что умеет делать SeoHammer
    — Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
    — Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
    — Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
    — SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
    SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней.
    Зарегистрироваться и Начать продвижение

    C & М = сканер & монитор 50

    (П | C) & М = (принтер | сканер) & монитор?

      С П М П | С П & М C & М (П | C) & М
    ?              
    ?              
    ?              
    ?              
    ?              
    ?              
                   
                   
    всего              

    6) проанализируем столбец П | С в этой таблице: его сумма (450) складывается из суммы столбцов С (200) и П (250) – выделены ярким зеленым цветом – плюс последние две строчки (голубой фон), то есть, 450 = 200 + 250 + X, откуда сразу получаем, что X = 0, то есть, последним двум строчкам (запросам) не удовлетворяет ни одного сайта

    7) теперь составим таблицы истинности для остальных запросов, отбросив заведомо «нулевые» варианты:

      С П М П | С П & М C & М (П | C) & М
    ?              
    ?              
    ?              
                   
    ?              
                   
    всего              

    из оставшихся шести строк таблицы запросы П & М и С & М затрагивают только по одной строчке, поэтому сразу можем вписать соответствующие числа в первый столбец; в последнем запросе, который нас интересует, присутствуют именно эти две строки, то есть, для получения нужно сложить 40 и 50

    8) таким образом, правильный ответ: 40 + 50 = 90.

    Решение (вариант 3, через диаграммы и систему уравнений):

    1) для сокращения записи обозначим через C, П, М высказывания «ключевое слово на сайте – сканер» (соответственно принтер, монитор) и нарисуем эти области виде диаграммы (кругов Эйлера); интересующему нас запросу (П | C) & M соответствует объединение областей 4, 5 и 6 («зеленая зона» на рисунке)

    2) количество сайтов, удовлетворяющих запросу в области i, будем обозначать через Ni

    3) составляем уравнения, которые определяют запросы, заданные в условии:

    сканер N1 + N2 + N4 + N5 = 200

    принтер N2 + N3 + N5 + N6 = 250

    принтер | сканер N1 + N2 + N4 + N5 + N3 + N6 = 450

    из первого и третьего уравнений сразу следует

    200 + N3 + N6 = 450 Þ N3 + N6 = 250

    далее из второго уравнения

    N2 + N5 + 250 = 250 Þ N2 + N5 = 0

    поскольку количество сайтов не может быть отрицательной величиной, N2 = N5 = 0

    4) посмотрим, что еще мы знаем (учитываем, что N5 = 0):

    принтер & монитор N5 + N6 = 40 Þ N6 = 40

    сканер & монитор N4 + N5 = 50 Þ N4 = 50

    5) окончательный результат:

    (принтер | сканер) & монитор N4 + N5 + N6 = N4 + N6 = 40 + 50 = 90

    6) таким образом, правильный ответ 90.

    Возможные проблемы: · внимательнее с индексами переменных, очень легко по невнимательности написать N5 вместо N6 и получить совершенно другой результат · этот метод ярко демонстрирует, что в общем случае мы получаем систему уравнения с семью неизвестными (или даже с восемью, если задействована еще и область вне всех кругов); решать такую систему вручную достаточно сложно, поэтому на экзамене всегда будет какое-то условие, сильно упрощающее дело, ищите его

    Еще пример задания:

    В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

      Запрос Количество страниц (тыс.)
      мезозой    
      кроманьонец    
      неандерталец    
      мезозой | кроманьонец    
      мезозой | неандерталец    
      неандерталец & (мезозой | кроманьонец)    

    Сколько страниц (в тысячах) будет найдено по запросу

    кроманьонец & (мезозой | неандерталец)

    Решение (способ 1, круги Эйлера):

    1) обозначим области «мезозой», «кроманьонец» и «неандерталец» буквами М, К и Н; пронумеруем подобласти, получившиеся в результате пересечений кругов (см. рисунок справа)

    Сервис онлайн-записи на собственном Telegram-боте
    Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
    — Разгрузит мастера, специалиста или компанию;
    — Позволит гибко управлять расписанием и загрузкой;
    — Разошлет оповещения о новых услугах или акциях;
    — Позволит принять оплату на карту/кошелек/счет;
    — Позволит записываться на групповые и персональные посещения;
    — Поможет получить от клиента отзывы о визите к вам;
    — Включает в себя сервис чаевых.

    Для новых пользователей первый месяц бесплатно.
    Зарегистрироваться в сервисе

    2) через N­i обозначим количество сайтов в области с номером i

    3) нас интересует результат запроса

    кроманьонец & (мезозой | неандерталец)

    то есть N­2 + N5 + N6(зеленая область на рисунке)

    4) из первых двух запросов следует, что

    N1 + N2 + N4 + N5 = 50 (мезозой)

    N2 + N3 + N5 + N6 = 60 (кроманьонец)

    5) складывая левые и правые части уравнений, получаем

    (1) N1 + 2·N2 + N3 + N4 + 2·N5 + N6 = 110

    6) в то же время из запроса 4 получаем

    (2) N1 + N2 + N3 + N4 + N5 + N6 = 80 (мезозой | кроманьонец)

    7) вычитая из уравнения (1) уравнение (2), отдельно левые и правые части, получаем

    N2 + N5 = 30 (мезозой & кроманьонец)

    вспомним, что наша цель – определить N­2 + N5 + N6, поэтому остается найти N6

    8) из запросов 1 и 3 следует, что

    N1 + N2 + N4 + N5 = 50 (мезозой)

    N4 + N5 + N6 + N7 = 70 (неандерталец)

    9) складывая левые и правые части уравнений, получаем

    (3) N1 + N2 + 2·N4 + 2·N5 + N6 + N7 = 120

    10) в то же время из запроса 5 получаем

    (4) N1 + N2 + N4 + N5 + N6 + N7 = 100 (мезозой | неандерталец)

    11) вычитая из уравнения (3) уравнение (4), отдельно левые и правые части, получаем

    (5) N4 + N5 = 20 (мезозой & неандерталец)

    12) теперь проанализируем запрос 6:

    неандерталец & (мезозой | кроманьонец)

    (6) N4 + N5 + N­6 = 20

    13) вычитая из уравнения (6) уравнение (5) получаем N6 = 0, поэтому

    N2 + N5 + N6 = N2 + N5 = 30

    14) таким образом, ответ – 30.

    Решение (способ 2, М.С. Коротков, г. Челябинск, Лицей № 102):

    1) пп. 1-3 такие же, как в первом способе;

    2) из запросов 1 и 6 следует, что

    (1) N4 + N5 + N6 + N7 = 70 (неандерталец)

    (2) N4 + N5 + N­6 = 20 неандерталец & (мезозой | кроманьонец)

    3) вычитая (2) из (1), сразу получаем, что N7 = 50

    4) из запросов 5 и 4 следует, что

    (3) N1 + N2 + N4 + N5 + N6 + N7 = 100 (мезозой | неандерталец)

    (4) N1 + N2 + N3 + N4 + N5 + N6 = 80 (мезозой | кроманьонец)

    5) вычитая (4) из (3), сразу получаем, что N7 - N3 = 20

    6) в п. 3 мы уже определили, что N7 = 50, поэтому 50 - N3 = 20, откуда N3 = 30

    7) из запроса 2 получаем

    N2 + N3 + N5 + N6 = 60 (кроманьонец)

    поэтому размер интересующей нас области равен

    N2 + N5 + N6 = 60 – N3 = 60 – 30 = 30

    8) таким образом, ответ – 30.

    Решение (способ 3, круги Эйлера, И.Б. Курбанова, г. Санкт-Петербург, ГОУ СОШ № 594):

    1) обозначим: М – мезозой, К – кроманьонец, Н – неандерталец.

    2) нас интересует результат запроса (см. диаграмму Эйлера)

    K & (M | Н)

    3) 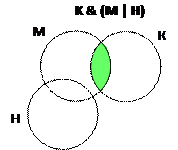т.к. по условию М = 50, К = 60, а объединение этих множеств М | К = 80, можно сделать вывод, что область пересечения

    M & K = 50 + 60 – 80 = 30;

    4) т.к. по условию М = 50, Н = 70, а объединение этих множеств М | Н = 100, можно сделать вывод, что область пересечения

    M & Н = 50 + 70 – 100 = 20;

    5) заметим, что M & Н = 20 и Н & (М | К) = 20, следовательно множества Н и К не пересекаются (К & Н = 0);

    6) перерисуем диаграмму Эйлера так, чтобы множества К и Н не пересекались (см. рисунок справа); из новой схемы видно, что

    К & (М | Н) = (К & М) | (К & Н) = К & М = 30

    7) ответ: 30


    Задачи для тренировки[3]:

    Во всех задачах для обозначения логической операции «ИЛИ» в запросе используется символ |, а для логической операции «И» – символ &.

    1) В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.

    А) физкультура

    Б) физкультура & подтягивания & отжимания

    В) физкультура & подтягивания

    Г) физкультура | фитнесс

    2) В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.

    А) волейбол | баскетбол | подача

    Б) волейбол | баскетбол | подача | блок

    В) волейбол | баскетбол

    Г) волейбол & баскетбол & подача

    3) В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.

    A) чемпионы | (бег & плавание)

    Б) чемпионы & плавание

    В) чемпионы | бег | плавание

    Г) чемпионы & Европа & бег & плавание

    4) В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.

    А) музыка | классика | Моцарт | серенада

    Б) музыка | классика

    В) музыка | классика | Моцарт

    Г) музыка & классика & Моцарт

    5) В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.

    А) реферат | математика | Гаусс

    Б) реферат | математика | Гаусс | метод

    В) реферат | математика

    Г) реферат & математика & Гаусс

    6) В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Ответ запишите в виде последовательности соответствующих букв.

    a) Америка | путешественники | Колумб

    b) Америка | путешественники | Колумб | открытие

    c) Америка | Колумб

    d) Америка & путешественники & Колумб

    7) В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу. Ответ запишите в виде последовательности соответствующих букв.

    а) Информатика & уроки & Excel

    b) Информатика | уроки | Excel | диаграмма

    с) Информатика | уроки | Excel

    d) Информатика | Excel

    8) В таблице приведены запросы к поисковому серверу, условно обозначенные буквами от А до Г. Расположите запросы в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Ответ запишите в виде последовательности соответствующих букв.

    А) Гренландия & Климат & Флора & Фауна

    Б) Гренландия & Флора

    В) (Гренландия & Флора) | Фауна

    Г) Гренландия & Флора & Фауна

    9) В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.

    а) спорт | футбол

    b) спорт | футбол | Петербург | Зенит

    с) спорт | футбол | Петербург

    d) спорт & футбол & Петербург & Зенит

    10) Каким условием нужно воспользоваться для поиска в сети Интернет информации о цветах, растущих на острове Тайвань или Хонсю

    1) цветы & (Тайвань | Хонсю)

    2) цветы & Тайвань & Хонсю

    3) цветы | Тайвань | Хонсю

    4) цветы & (остров | Тайвань | Хонсю)

    11) Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:

    Ключевое слово Количество сайтов, для которых данное слово является ключевым
    сомики 250
    меченосцы 200
    гуппи 500

    Сколько сайтов будет найдено по запросу

    сомики | меченосцы | гуппи

    если по запросу сомики & гуппи было найдено 0 сайтов, по запросу
    сомики & меченосцы – 20, а по запросу меченосцы & гуппи – 10.

    12) Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:

    Ключевое слово Количество сайтов, для которых данное слово является ключевым
    сомики 250
    меченосцы 200
    гуппи 500

    Сколько сайтов будет найдено по запросу

    (сомики & меченосцы) | гуппи

    если по запросу сомики | гуппи было найдено 750 сайтов, по запросу сомики & меченосцы – 100, а по запросу меченосцы & гуппи – 0.

    13) Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:

    Ключевое слово Количество сайтов, для которых данное слово является ключевым
    сканер 200
    принтер 250
    монитор 450

    Сколько сайтов будет найдено по запросу

    принтер | сканер | монитор

    если по запросу принтер | сканер было найдено 450 сайтов, по запросу принтер & монитор – 40, а по запросу сканер & монитор – 50.

    14) В таблице приведены запросы к поисковому серверу, условно обозначенные буквами от А до Г. Расположите запросы в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Ответ запишите в виде последовательности соответствующих букв.

    А) (огурцы & помидоры) & (прополка | поливка)

    Б) огурцы | помидоры

    В) огурцы

    Г) огурцы & помидоры

    15) В таблице приведены запросы к поисковому серверу, условно обозначенные буквами от А до Г. Расположите запросы в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Ответ запишите в виде последовательности соответствующих букв.

    А) экзамен | тестирование

    Б) (физика | химия) & (экзамен | тестирование)

    В) физика & химия & экзамен & тестирование

    Г) физика | химия | экзамен | тестирование

    16) В таблице приведены запросы к поисковому серверу, условно обозначенные буквами от А до Г. Расположите запросы в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Ответ запишите в виде последовательности соответствующих букв.

    А) сомики | меченосцы | содержание

    Б) сомики & содержание

    В) сомики & меченосцы & разведение & содержание

    Г) (сомики | меченосцы) & содержание

    17) В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения логической операции «ИЛИ» в запросе используется символ |, а для логической операции «И» – &.

    1) канарейки | щеглы | содержание

    2) канарейки & содержание

    3) канарейки & щеглы & содержание

    4) разведение & содержание & канарейки & щеглы

    18) В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения логической операции «ИЛИ» в запросе используется символ |, а для логической операции «И» – &.

    1) барокко | (классицизм & ампир)

    2) барокко | классицизм

    3) барокко | ампир | классицизм

    4) классицизм & ампир

    19) В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения логической операции «ИЛИ» в запросе используется символ |, а для логической операции «И» – &.

    1) барокко | (классицизм & ампир)

    2) барокко | классицизм

    3) (классицизм & ампир) | (барокко & модерн)

    4) барокко | ампир | классицизм

    20) В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения логической операции «ИЛИ» в запросе используется символ |, а для логической операции «И» – &.

    1) зайцы & кролики

    2) зайцы & (кролики | лисицы)

    3) зайцы & кролики & лисицы

    4) кролики | лисицы

    21) В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения логической операции «ИЛИ» в запросе используется символ |, а для логической операции «И» – &.

    1) кролики | лисицы

    2) (зайцы & кролики) | (лисицы & волки)

    3) зайцы & кролики & лисицы & волки

    4) зайцы & кролики

    22) В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения логической операции «ИЛИ» в запросе используется символ |, а для логической операции «И» – &.

    1) шкафы | столы | стулья

    2) шкафы | (стулья & шкафы)

    3) шкафы & столы

    4) шкафы | стулья

    23) В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения логической операции «ИЛИ» в запросе используется символ |, а для логической операции «И» – &.

    1) яблоки | сливы

    2) сливы | (сливы & груши)

    3) яблоки | груши | сливы

    4) (яблоки | груши) & сливы

    24) В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

    Запрос Количество страниц (тыс.)
    фрегат | эсминец 3000
    фрегат 2000
    эсминец 2500

    Сколько страниц (в тысячах) будет найдено по запросу

    фрегат & эсминец

    25) В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

    Запрос Количество страниц (тыс.)
    фрегат & эсминец 500
    фрегат 2000
    эсминец 2500

    Сколько страниц (в тысячах) будет найдено по запросу

    фрегат | эсминец

    26) В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

    Запрос Количество страниц (тыс.)
    фрегат & эсминец 500
    фрегат | эсминец 4500
    эсминец 2500

    Сколько страниц (в тысячах) будет найдено по запросу

    Фрегат

    27) В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

    Запрос Количество страниц (тыс.)
    крейсер | линкор 7000
    крейсер 4800
    линкор 4500

    Сколько страниц (в тысячах) будет найдено по запросу

    крейсер & линкор

    28) В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

    Запрос Количество страниц (тыс.)
    торты | пироги 12000
    торты & пироги 6500
    пироги 7700

    Сколько страниц (в тысячах) будет найдено по запросу

    Торты

    29) В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

     

    Запрос Количество страниц (тыс.)
    пирожное | выпечка 14200
    пирожное 9700
    пирожное & выпечка 5100

    Сколько страниц (в тысячах) будет найдено по запросу


    ⇐ Предыдущая1234Следующая ⇒




    © 2023 :: MyLektsii.ru :: Мои Лекции
    Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав.
    Копирование текстов разрешено только с указанием индексируемой ссылки на источник.